力扣刷题笔记12-二叉树系列（2)

1.递增顺序搜索树

 

 

 

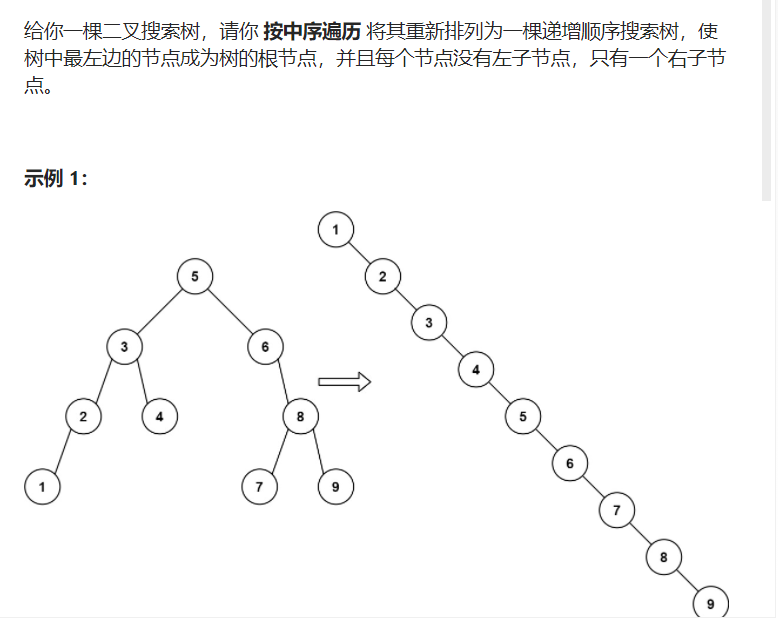
解题思路：这道题非常简单，题目已经告诉要使用中序遍历了，所以我们只需中序遍历二叉搜索树，并把遍历后的值按顺序放入vector中，

然后根据数组中的节点值，创建等价的只含有右节点的二叉搜索树，其过程等价于根据节点值创建一个链表。具体代码如下：

 

 

 

 

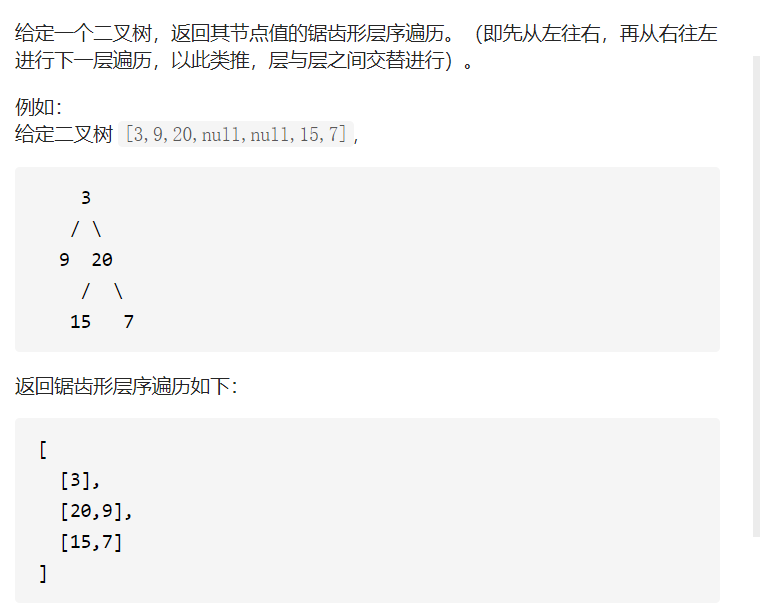
2.二叉树的锯齿形层次遍历

 

 

解题思路：这道题就是二叉树层次遍历的一个变型，我们只需在层次遍历基础上增加一个变量num记录该层的位于第几层，每遍历一层就要判断num是否是偶数，

如果是偶数就要将该层的vector中元素翻转。否则保持不变，最后将该层的vector数组压入到结果vecor中。具体代码如下：

 

 

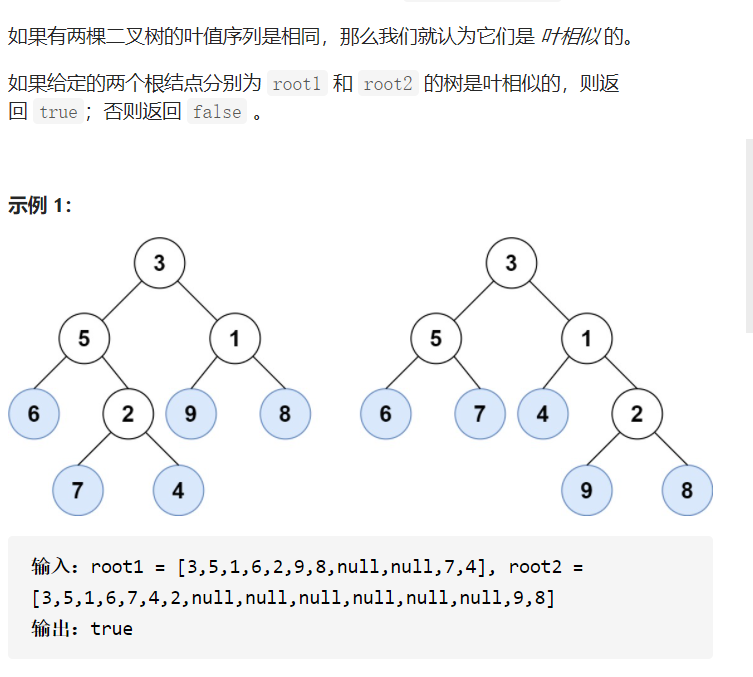
3.叶子相似的树

 

 

解题思路：这道题也是一道简单题，我们只需遍历一遍二叉树（我使用的是中序遍历），然后将树中的叶子节点存放到一个vector中，

然后判断两个vector是否相等即可。具体代码如下：

 

 

4.二叉树的堂兄弟结点

 

 

 

解题思路：这道题使用层次遍历比较方便，我们可以定义两个变量father1和father2(初始值都为-1）来记录两个目标结点的父节点在上一层的位置，

每经过一层的遍历就要进行一次判断。如果找到了目标结点且 father1!=father2&&father1!=-1&&father2=-1 则可以返回true，否则返回false。具体代码

如下所示：

 

 

5.二叉树的最近公共祖先

 

 

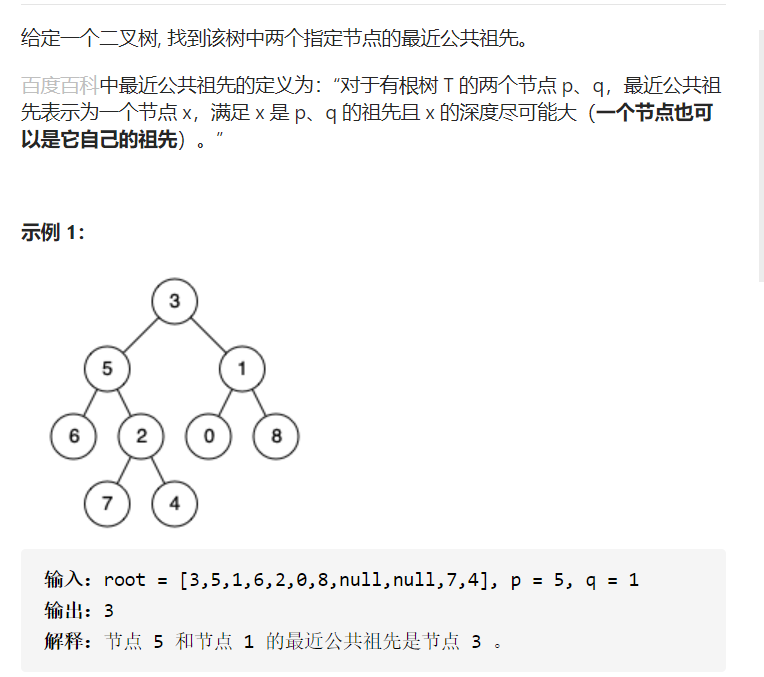
解题思路：

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。后序遍历就是天然的回溯过程，最先处理的一定是叶子节点。

接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，

那么该节点就是节点p和q的最近公共祖先。使用后序遍历，回溯的过程，就是从低向上遍历节点，一旦发现如何这个条件的节点，就是最近公共节点了。

递归三部曲：

确定递归函数返回值以及参数
需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。但我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

代码如下：TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)

确定终止条件
如果找到了 节点p或者q，或者遇到空节点，就返回。代码如下：if (root == q || root == p || root == NULL) return root;

完整代码如下：

 

6.从前序与中序遍历序列构造二叉树

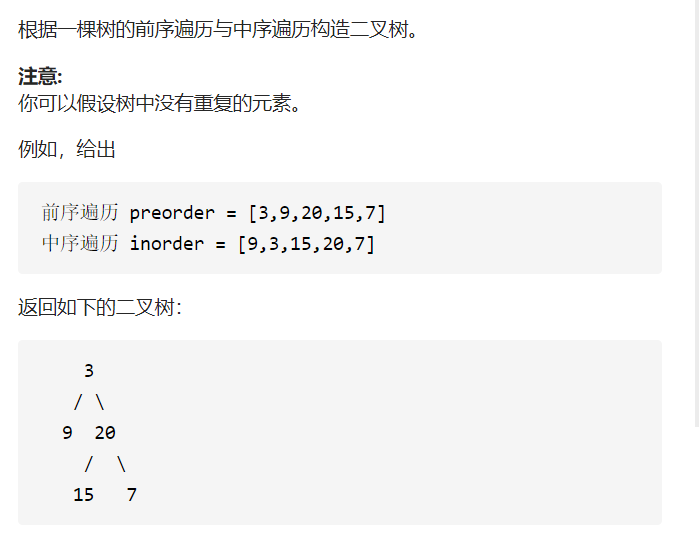
解题思路：

 重建二叉树的基本思路就是先构造根节点，再构造左子树，接下来构造右子树，其中，构造左子树和右子树是一个子问题，递归处理即可。因此我们只关心如何构造根节点，以及如何递归构造左子树和右子树。

递归函数的设计上，仍旧采用**左闭右闭**对数组局部进行描述。即一个数组，使用 3 个变量描述：

• 数组本身 arr
• 数组的起始位置 lo
• 数组的结束位置 hi

因此，数组实际元素就是 arr[lo..hi] 这个范围（注意这是一个左闭右闭的区间，如果你喜欢左闭右开区间，那你可能重新考虑一下 lo、hi 的值如何计算）

接下来，很自然的就是写出递归函数原型 TreeNode* buildTree(vector<int>& preorder, int lo1, int hi1, vector<int>& inorder, int lo2, int hi2)，它的主要参数相比原来题目中的原型多了数组范围描述变量，这是我们所期望的，因为我们要做区间分治嘛。

后面的故事就很简单了，三元组 (preorder, lo1, hi1) 描述的前序遍历数组，以及三元组 (inorder, lo2, hi2) 描述的中序遍历数组，如何从它们重建二叉树？递归的说法就是：

• 创建根节点
• 递归创建左子树
• 递归创建右子树

你会发现，递归创建左子树，无非就是再构造一个新的前序遍历的三元组 (preorder, lo1+1, lo1+mid-lo2) 以及 (inorder, lo2, mid-1)，其中 mid 是当前 inorder 中 root 的位置，创建右子树无非是(preorder,lo1+mid-lo2+1,right1)和 (inorder, mid+1,right2)。

具体代码如下：

 

 

 

7.二叉搜索树与双向链表

 

 

 

 

 

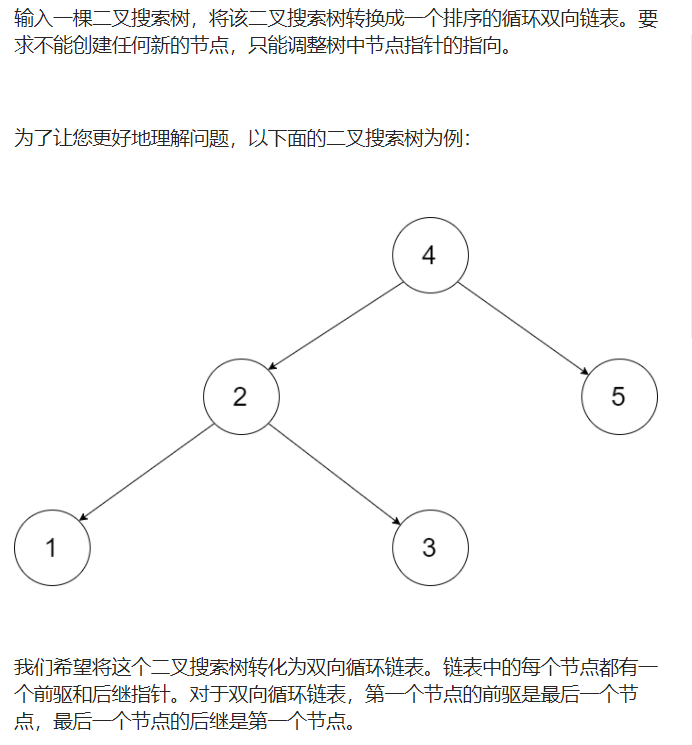
 解题思路：

1.这里定义全局的head和pre。
2.整体思路按照中序遍历来走，pre如果为空则表示是这棵树左下的节点，那么将其定义为头节点。
3.如果pre不空的话，就表示当前遍历的节点的左子树的右下节点。
4.遍历完成后，pre指向这棵树右下的节点。
5.最后将其首尾连接起来。

具体代码如下：