力扣刷题笔记11-二叉树系列（1)

1.二叉树的前序遍历

 

 

 

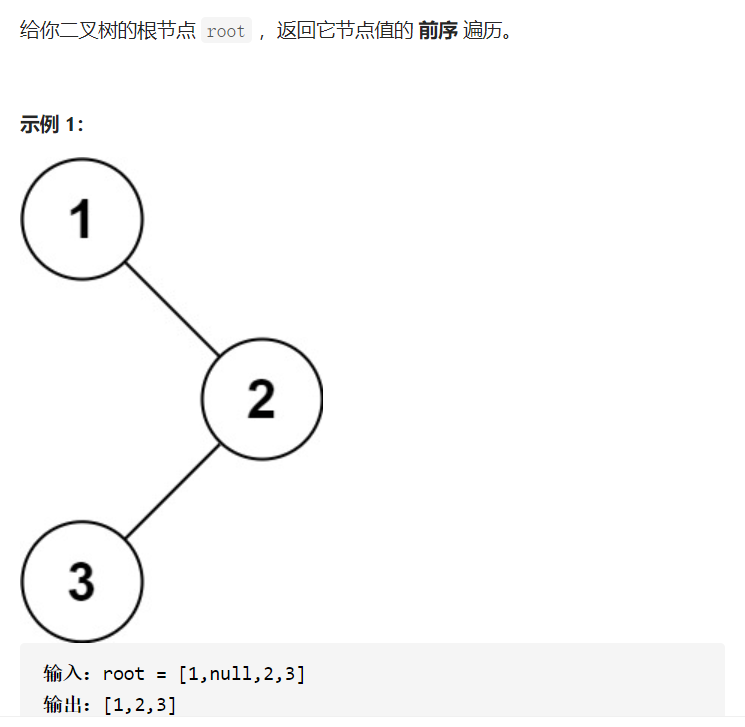
解题思路：

前序遍历的顺序是, 对于树中的某节点,先遍历该节点,然后再遍历其左子树,最后遍历其右子树.

中序遍历的顺序是, 对于树中的某节点,先遍历其左子树该节点,然后再遍历该节点,最后遍历其右子树.

后序遍历的顺序是, 对于树中的某节点,先遍历其左子树该节点,然后再遍历其右子树,最后遍历该节点.

所以对于二叉树的前序，中序，后序遍历来说，使用递归是最方便的方法，具体代码如下：

 

 

 

 

2.二叉树的层次遍历

 

 

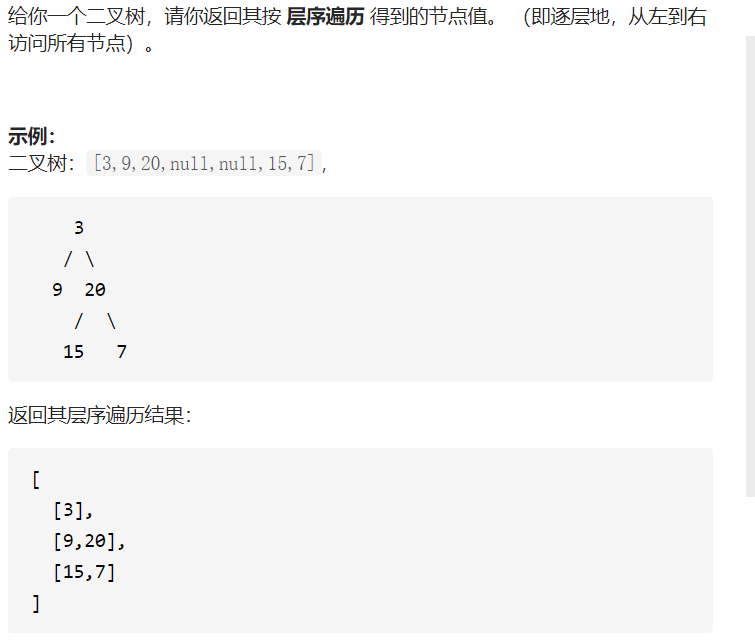
 解题思路如下：

二叉树的层序遍历，顾名思义就是对一棵二叉树一层一层的遍历它的节点，因此可以使用 BFS进行遍历。显然起点是 root 根节点，首先将起点 root 加入队列，在队列 q 不为空的情况下，遍历当前队列中的所有节点（相当于是遍历本层的所有节点，并全部添加到一个vector 集合中），然后将本层的每个节点扩散得到下一层的所有节点，并把扩散得到的所有节点全部添加到队列 q 中，然后不断重复，直到整棵树遍历完成为止。

代码如下：

 

 

 

 

3.二叉树的深度

 

 

解题思路如下：这道题我使用的是层次遍历，即没经过一层，res++（res表示的就是树的深度，初始值为0）

 

代码如下：

 

 

 

4.二叉树的层平均值

解题思路如下：

这道题本质还是考察二叉树的层次遍历，在对二叉树每一层遍历的时候记录该层的结点val的总和，并且记录该层节点总个数，然后相除放入vector中即可

代码如下：

 

 

5.二叉树的右视图

 

 

 

 

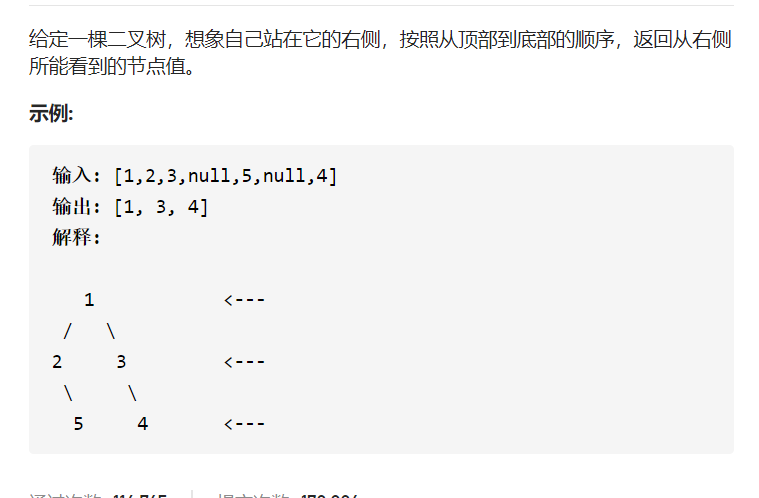
解题思路如下：这道题我还是使用的层次遍历方法，因为层次遍历要对每一层进行遍历，while语句中的for循环作用就是

这个，因此在for循环中只要加一个判断段语句：if（i==该层节点数目-1），就将队列此时的头结点的值插入到结果数组中，

因为此时的头结点就是该层最后一个结点，即最右的结点。

具体代码如下：

 

 

 

6.反转链表

 

 

 解题思路：这道题可以用递归法和迭代法两种方法，具体解题思路如下

1.递归法：

我们从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root 为根节点的整棵子树的翻转

代码如下：

 

 

 2.迭代法

迭代法理解起来要比递归法容易，即直接对每一层节点的左右孩子在树中进行交换，再将交换后的该层结点的左右孩子结点压入队列中

代码如下

 

7.相同的数

 

 

 

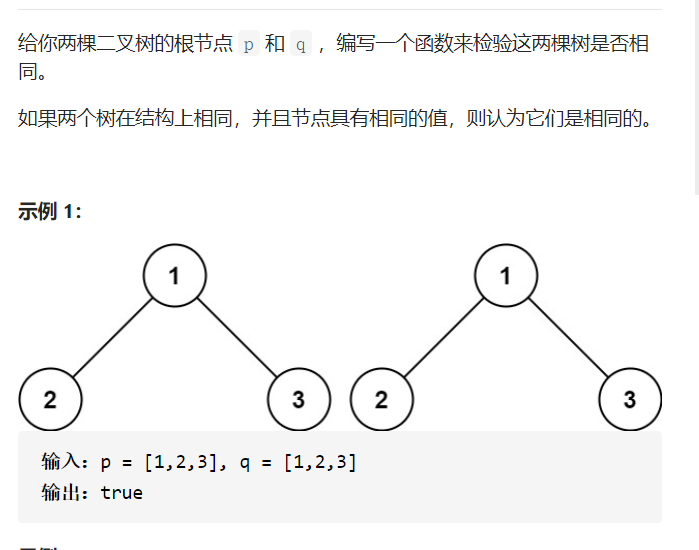
解题思路如下：

如果两个二叉树都为空，则两个二叉树相同。如果两个二叉树中有且只有一个为空，则两个二叉树一定不相同。

如果两个二叉树都不为空，那么首先判断它们的根节点的值是否相同，若不相同则两个二叉树一定不同，若相同，再分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程，因此可以使用深度优先搜索，递归地判断两个二叉树是否相同。

具体代码如下：

 

 

 

8.另一棵树的子树

 

 

解题思路：这道题是上一道题的延申，只不过我们需要加一层递归，遍历s树的结点，如果该结点的值和t树的root结点的值相同则带入到上一题的代码(判断以该节点为root的树和t树是否相同)

如果相同返回true，否则继续遍历s的结点，直到所有节点遍历完，返回false。

代码如下：

 

 

9.平衡二叉树

 

解题思路如下：这道题是在求二叉树深度的题目上延伸的，在这里我们也是使用的递归方法。具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，

如果左右子树的高度差是否不超过 1，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。

具体代码如下：

 

 

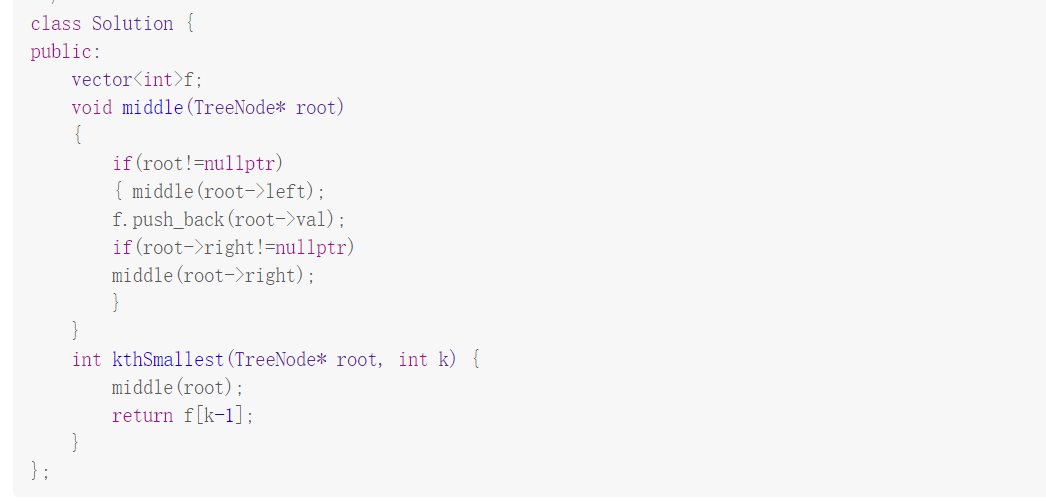
 10.二叉搜索树中最小的第k个元素

 

解题思路：因为中序遍历二叉搜索树时，产生的vector就是按照从小到大的顺序排列的，所以我们只需中序遍历搜索树，存入到vector中，然后访问第k-1个结点即可。

代码如下：

 

 

11.二叉树的第k个最大结点

 

 

 

解题思路：这道题和上道题几乎一样，只不过一个是求最大的第k个结点，一个是求最小的第k个结点。所以我们只需要

逆置二叉树的中序遍历即可，剩下的就和上题一样了。但是我们可以再上道题的基础上进行优化。具体过程如下：

首先设置count=k；

 

终止条件： 当节点 root为空（越过叶节点），则直接返回；
递归右子树： 即 dfs(root.right)；
三项工作：
提前返回:若 count = 0 ,代表已找到目标节点，无需继续遍历，因此直接返回；
统计序号:执行 count = count - 1 （即从 count 减至 0 ）；
记录结果: 若 count = 0，代表当前节点为第 k 大的节点，因此记录 res = root.val；
递归左子树:即 dfs(root.left) ；

 

代码如下：

 

 12.二叉树的完全性检验

 

解题思路：这道题我们可以使用层次遍历来解决，因为由题意可知如果我们使用层次遍历完全二叉树，最后一个结点肯定是null，也可以说

如果在遍历的过程中如果发现null结点后还有不为null的结点，该树就不是完全二叉树，具体解题代码如下所示