几种经典排序算法

1.选择排序

原理：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法

 

具体代码如下：

 

 

 

2.冒泡排序

具体步骤为：

       （1）比较相邻的两个数，如果第一个数比第二个数大，则两数交换。

       （2）对之后的相邻元素进行同样的工作，从开始到最后一对，这样进行一次排序后，数据的最后一位会是最大值 ，第一次循环进行的次数为 arr.length-1。

       （3）之后对所有的元素重复以上的步骤，且以后每次循环的次数为arr.length-1-i （i为循环第几次 ，i 从零开始）；

       （4）重复上述步骤，直到排序完成

具体代码如下：

 

 

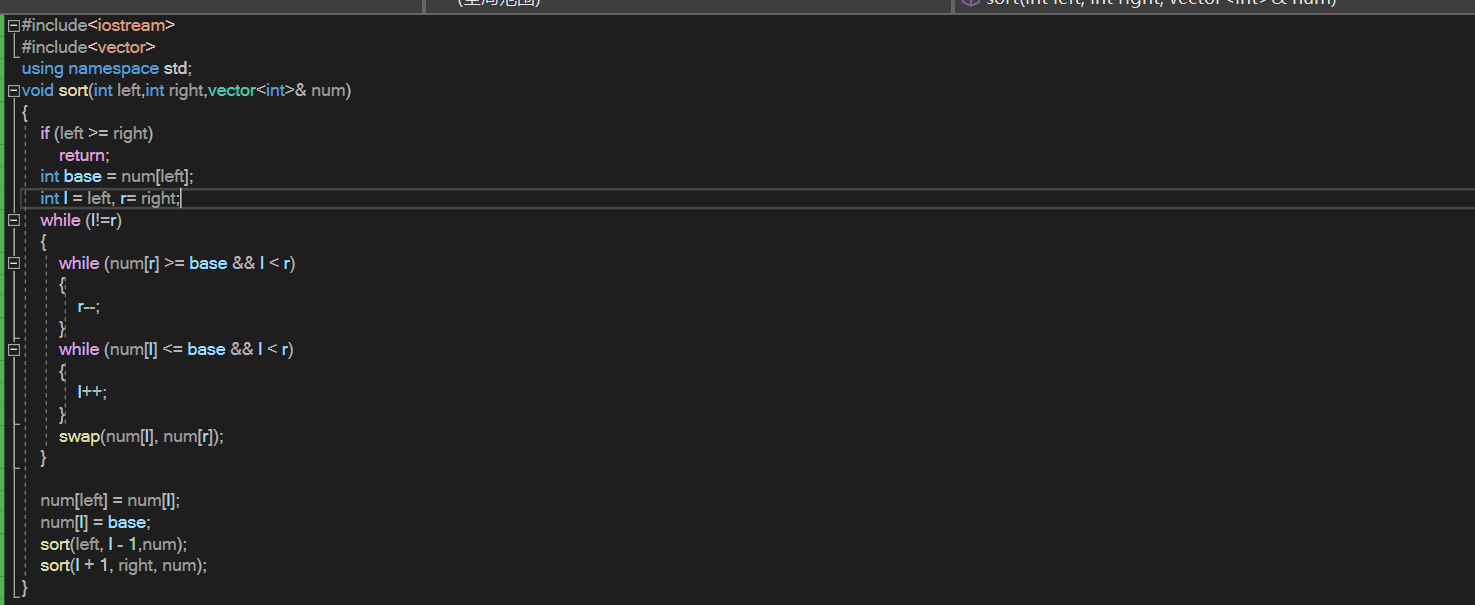
3.快速排序

 

具体过程如下：

(1)首先设定一个分界值，通过该分界值将数组分成左右两部分。

(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。 

 

具体代码如下：

 

 

 

 

 

   

 

 

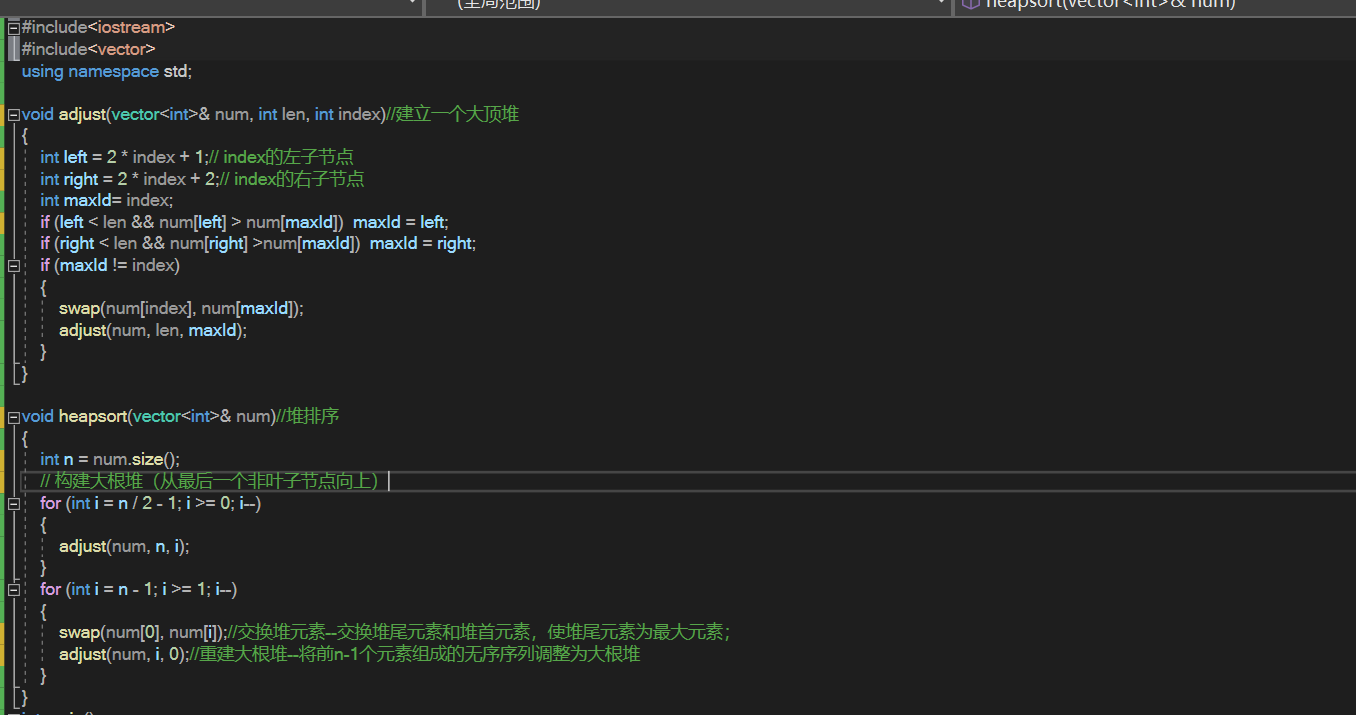
4.堆排序

 

具体过程如下：

（1）建立大根堆或小顶堆（为了方便后面统一使用大顶堆）--将n个元素组成的无序序列构建一个大根堆。

（2）交换堆元素--交换堆尾元素和堆首元素，使堆尾元素为最大元素；

（3）重建大根堆--将前n-1个元素组成的无序序列调整为大根堆

（4）重复执行步骤二和步骤三，直到整个序列有序。

具体代码如下：