Codeforces Pinely Round 1 CF 1761 A B C D E 题解
A. Two Permutations
首先n=a=b的情况是合法的。其余的情况,如果\(a+b \ge n\),显然矛盾,因为这样前缀和后缀相等的长度应该都是n才对。\(a+b=n-1\)也不行,因为题目中要求的是排列,这种情况下a和b也应该都是n才对。其它情况都是合法的。
时间复杂度\(O(1)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nPROGRAM TERMINATED";
#endif
exit(0);
}
using namespace std;
int t,n,a,b;
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n>>a>>b;
if(n==a&&n==b) puts("Yes");
else cout<<(a+b<n-1 ? "Yes":"No")<<endl;
}
termin();
}
B. Elimination of a Ring
n=1的情况答案是1。否则,如果整个序列只有两种不同数字交替出现,那答案显然是\(\frac n2+1\)。其余情况答案就是n,考虑证明:假设序列中的不同数字从小到大为1,2,3……,那先把所有1拿出来,如果只有一个1,那可以每次删掉1旁边的一个数,做到操作数为n;否则,任意两个1之间夹着的一段,都可以通过不断删掉跟1挨着的某一个从而使得段中剩下任意恰好一个数,由于这种情况不同数字个数至少为3,一定可以合理选择每一段剩下的那一个数,使得有相邻的某两段剩下的数不同,把这两段之间的那个1删掉,直到整个序列只剩下一个1就行了。
时间复杂度\(O(n)\)或\(O(nlogn)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nPROGRAM TERMINATED";
#endif
exit(0);
}
using namespace std;
int t,n,a[110];
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n;
rep(i,n) cin>>a[i];
if(n==1)
{
puts("1");
continue;
}
set <int> ss,tt;
rep(i,n)
{
if(i%2) ss.insert(a[i]);
else tt.insert(a[i]);
}
if(ss.size()==1&&tt.size()==1) cout<<n/2+1<<endl;
else cout<<n<<endl;
}
termin();
}
C. Set Construction
题目保证输入的有向图有解,所以这个图满足:任意两点间如果有路径,那么它们之间一定直接有边相连,类似一个传递闭包的形式。考虑如下构造:点i的set里包含数j,当且仅当i=j或点j到点i直接有边。这样是对的,因为如果两个点x,y,x到y有边,那么x的set肯定是y的真子集;如果x和y之间没有路径,那么x的集合里不包含数y,y的集合里也不包含数x,也是满足条件的。
时间复杂度\(O(n^2)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nPROGRAM TERMINATED";
#endif
exit(0);
}
using namespace std;
int t,n;
string s[110];
vector <int> ans[110];
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n;
rep(i,n) cin>>s[i],ans[i+1].clear();
rep(i,n) rep(j,n) if(s[i][j]=='1') ans[j+1].pb(i+1);
repn(i,n) ans[i].pb(i);
repn(i,n)
{
cout<<ans[i].size()<<' ';
rep(j,ans[i].size()) printf("%d ",ans[i][j]);
puts("");
}
}
termin();
}
D. Carry Bit
手动模拟一下小学里学的竖式计算的过程,发现会发生进位的位置是满足如下条件的:
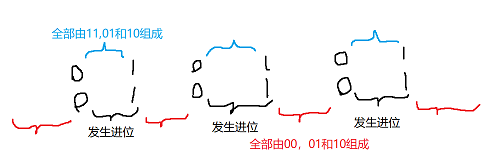
我们枚举两个序列中\(00 \to 11\)的区间的数量,把剩下的需要进位的位置和不需要进位的位置用插板法插入进去就行了。注意到除了这些区间的端点,其余的每个位置都有3种选法,快速幂或者预处理都行。还有一种情况是最左边的一个\(00 \to 11\)区间紧贴序列最左边,可以不需要区间左端点处的00,跟上面也是类似的。
时间复杂度\(O(n)\)或\(O(nlogn)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nPROGRAM TERMINATED";
#endif
exit(0);
}
using namespace std;
const LL MOD=1e9+7;
LL qpow(LL x,LL a)
{
LL res=x,ret=1;
while(a>0)
{
if(a&1) (ret*=res)%=MOD;
a>>=1;
(res*=res)%=MOD;
}
return ret;
}
LL n,k,fac[2000010],inv[2000010];
LL C(LL nn,LL mm){return fac[nn]*inv[mm]%MOD*inv[nn-mm]%MOD;}
LL separ(LL nn,LL mm){return C(nn+mm-1,mm-1);}
int main()
{
fileio();
fac[0]=1;repn(i,2000005) fac[i]=fac[i-1]*i%MOD;
inv[2000003]=qpow(fac[2000003],MOD-2);
for(int i=2000002;i>=0;--i) inv[i]=inv[i+1]*(i+1)%MOD;
cin>>n>>k;
if(k==0)
{
cout<<qpow(3,n)<<endl;
termin();
}
LL ans=0;
repn(i,k)
{
if(n-i-i>=k-i)
{
LL val=separ(k-i,i)*qpow(3,k-i)%MOD;
(val*=separ(n-i-i-(k-i),i+1)*qpow(3,n-i-i-(k-i))%MOD)%=MOD;
(ans+=val)%=MOD;
}
if(n-i-i+1>=k-i)
{
LL val=separ(k-i,i)*qpow(3,k-i)%MOD;
(val*=separ(n-i-i+1-(k-i),i)*qpow(3,n-i-i+1-(k-i))%MOD)%=MOD;
(ans+=val)%=MOD;
}
}
cout<<ans<<endl;
termin();
}
E. Make It Connected
先把原图中的连通块处理出来,如果只有1个那答案就是0。否则如果有大小为1的连通块,答案是1,直接对这个点操作1次就行了。
其余的情况,如果有某一个连通块不是完全图,那肯定可以在这个连通块内找出一个点,用一次操作解决问题。考虑证明:称这个连通块内到块里面所有其它点都有边的点为坏点,其它的为好点。如果我们能找出这个连通块在原图上的一个生成树,并且有好点在叶子的位置,那么直接对这个好点操作就行了。如果连通块中没有坏点,随便取一棵生成树并取叶子即可。否则,随便找一个坏点当根,并把从它连出去的所有边作为树边,这时所有的好点都是叶子了,随便取一个即可。
剩下的情况就是每个连通块都是完全图了。显然,这种情况一次操作是解决不了的。如果只有两个连通块,那么唯一的方法是取较小的那个,并一个一个操作其中的节点,使图连通。否则,随便进行一次操作就能使图中的一个连通块变成不是完全图,用上面说的方法操作即可。这样是2次操作。
时间复杂度\(O(n^2logn)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nPROGRAM TERMINATED";
#endif
exit(0);
}
using namespace std;
int t,n,fa[4010],good[4010];
string s[4010];
char c[4010];
vector <int> g[4010],v[4010],tg[4010];
int Find(int x){return fa[x]==x ? x:fa[x]=Find(fa[x]);}
void swit(int x)
{
rep(i,n) if(i!=x)
{
if(s[x][i]=='0')
{
g[x].pb(i);
g[i].pb(x);
}
else
{
rep(j,g[x].size()) if(g[x][j]==i) g[x].erase(g[x].begin()+j);
rep(j,g[i].size()) if(g[i][j]==x) g[i].erase(g[i].begin()+j);
}
}
}
int dfs(int pos,int par)
{
rep(i,tg[pos].size()) if(tg[pos][i]!=par)
{
int val=dfs(tg[pos][i],pos);
if(val>-1) return val;
}
return (good[pos] ? pos:-1);
}
int getPoint(vector <int> pnts)
{
rep(i,n)
{
tg[i].clear();
fa[i]=i;
}
rep(i,pnts.size())
{
int u=pnts[i];
rep(j,g[u].size()) if(Find(u)!=Find(g[u][j]))
{
fa[Find(u)]=Find(g[u][j]);
tg[u].pb(g[u][j]);tg[g[u][j]].pb(u);
}
good[u]=(g[u].size()!=pnts.size()-1 ? 1:0);
}
return dfs(pnts[0],0)+1;
}
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n;
rep(i,n) scanf("%s",c),s[i]=c;
rep(i,n) fa[i]=i,g[i].clear(),v[i].clear();
rep(i,n) rep(j,n) if(s[i][j]=='1')
{
g[i].pb(j);
if(Find(i)!=Find(j)) fa[Find(i)]=Find(j);
}
rep(i,n) v[Find(i)].pb(i);
int cnt=0,sv;
rep(i,n) if(v[i].size()) ++cnt;
if(cnt==1)
{
puts("0");
continue;
}
sv=cnt;
bool have=false;
rep(i,n) if(v[i].size())
{
cnt=0;
rep(j,v[i].size()) cnt+=g[v[i][j]].size();
if(cnt!=v[i].size()*(v[i].size()-1))
{
puts("1");
printf("%d\n",getPoint(v[i]));
have=true;break;
}
if(v[i].size()==1)
{
printf("1\n%d\n",v[i][0]+1);
have=true;break;
}
}
if(!have)
{
if(sv==2)
{
pii mn=mpr(1e9,1e9);
rep(i,n) if(v[i].size()) mn=min(mn,mpr((int)v[i].size(),i));
printf("%d\n",mn.fi);
rep(i,mn.fi) printf("%d ",v[mn.se][i]+1);puts("");
}
else
{
puts("2");
rep(i,n) if(v[i].size())
{
swit(v[i][0]);
printf("%d ",v[i][0]+1);
vector <int> tmp={v[i][0]};
for(int j=i+1;j<n;++j) rep(k,v[j].size()) tmp.pb(v[j][k]);
printf("%d\n",getPoint(tmp));
break;
}
}
}
}
termin();
}
E和F的难度断层有点大啊



 浙公网安备 33010602011771号
浙公网安备 33010602011771号