[题解] Codeforces Dytechlab Cup 2022 1737 A B C D E 题解
求点赞
A. Ela Sorting Books
从前往后一位一位确定答案。用一个数组记录当前每个字母库存的数量,要确定答案的某一位时,枚举前\(min(\frac nk,26)\)个字母,找到第一个库存为0的字母,则当前这位的答案就是这个字母。然后把字典序在这个字母之前的字母库存都-1就行。最后把库存中剩下的字母随便塞进未塞满的块就行了。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
using namespace std;
int t,n,k,cnt[30];
string s,ans;
int main()
{
ios::sync_with_stdio(false);
cin>>t;
rep(tn,t)
{
cin>>n>>k>>s;
rep(i,29) cnt[i]=0;
rep(i,s.size()) ++cnt[s[i]-'a'];
ans="";
rep(i,k)
{
int rec=0;
rep(j,min(25,n/k))
{
if(cnt[j]==0) break;
--cnt[j];++rec;
}
ans.pb(rec+'a');
}
cout<<ans<<endl;
}
return 0;
}
B. Ela's Fitness and the Luxury Number
询问[l,r]中的Luxury数的个数,一看就知道用[1,r]中的减去[1,l-1]中的。假设一个Luxury数被表示成了\(a \cdot b\)的形式,其中\(a \leq b\)。题目要求\(a=\lfloor \sqrt{a\cdot b}\rfloor\),转化一下得到\(a \cdot b < (a+1)^2\),进一步得到\(a \leq b < a+2+\frac 1a\),也就是\(a \leq b \leq a+2\)。这对于所有的\(a \geq 1\)都满足。容易发现每个Luxury数都只能被一组合法的\(a,b\)表示,每组合法的\(a,b\)都能表示一个Luxury数。假设现在要询问[1,x]中的Luxury数个数,分别求出该区间中能表示成\(a^2,a(a+1),a(a+2)\)的数的个数就行了。这里建议用二分,直接调用sqrt函数的话可能会有精度问题。
时间复杂度\(O(t\cdot log(l+r))\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
using namespace std;
LL t,l,r;
LL calc(LL c)
{
if(c==0) return 0;
LL ret=0;
LL lb=0,ub=1e9,mid;
while(lb<ub)
{
mid=(lb+ub+1)/2;
if(mid*mid<=c) lb=mid;
else ub=mid-1;
}
ret+=lb;
lb=0;ub=1e9;
while(lb<ub)
{
mid=(lb+ub+1)/2;
if(mid*mid+mid<=c) lb=mid;
else ub=mid-1;
}
ret+=lb;
lb=0;ub=1e9;
while(lb<ub)
{
mid=(lb+ub+1)/2;
if(mid*(mid+2)<=c) lb=mid;
else ub=mid-1;
}
ret+=lb;
return ret;
}
int main()
{
cin>>t;
rep(tn,t)
{
scanf("%lld%lld",&l,&r);
printf("%lld\n",calc(r)-calc(l-1));
}
return 0;
}
C. Ela and Crickets
一眼丁真,鉴定为纯纯的傻*题。完全无法区分OI老手和菜鸡。
对于初始的L型,我们把他凹进去的那个位置,以及所有与这个位置横坐标、纵坐标的奇偶性都相同的位置称为"不可到达的"。手动操作几步,发现这些位置确实永远无法到达。
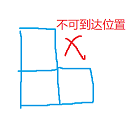
其他位置则是可到达的,大概长成这样:
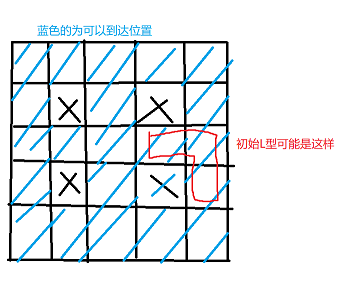
手玩一下发现对于任意的初始L型位置,所有的可到达位置都可以被走到。
有一个例外:当L型的中间一个位置在棋盘左上角时,只能走到第一行和第一列的位置。其他四个角同理:
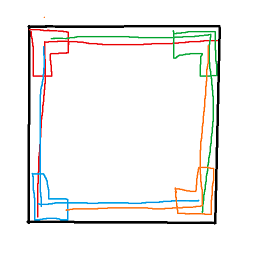
一个技巧:已知L型三个点的坐标,求凹进去那个点的坐标,直接把已知的三个点横纵坐标分别去异或就行了。
我一开始判L型在角上判错了,后来又发现有一个地方在一个询问内同时输出了YES和NO,直接导致这场打的和*一样。自闭.jpg
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
using namespace std;
int t,n,x,y;
pii r1,r2,r3;
int main()
{
cin>>t;
rep(tn,t)
{
cin>>n>>r1.fi>>r1.se>>r2.fi>>r2.se>>r3.fi>>r3.se;
cin>>x>>y;
int xx=r1.fi^r2.fi^r3.fi,yy=r1.se^r2.se^r3.se;
pii bad=mpr(1,1);
if((r1==bad||r2==bad||r3==bad)&&mpr(xx,yy)==mpr(2,2))
{
if(x==1||y==1) cout<<"YES\n";
else cout<<"NO\n";
continue;
}
bad=mpr(1,n);
if((r1==bad||r2==bad||r3==bad)&&mpr(xx,yy)==mpr(2,n-1))
{
if(x==1||y==n) cout<<"YES\n";
else cout<<"NO\n";
continue;
}
bad=mpr(n,1);
if((r1==bad||r2==bad||r3==bad)&&mpr(xx,yy)==mpr(n-1,2))
{
if(x==n||y==1) cout<<"YES\n";
else cout<<"NO\n";
continue;
}
bad=mpr(n,n);
if((r1==bad||r2==bad||r3==bad)&&mpr(xx,yy)==mpr(n-1,n-1))
{
if(x==n||y==n) cout<<"YES\n";
else cout<<"NO\n";
continue;
}
if(x%2==xx%2&&y%2==yy%2) cout<<"NO\n";
else cout<<"YES\n";
}
return 0;
}
D. Ela and the Wiring Wizard
一开始的"魔法"操作其实是,把一条边的一个端点沿着与其相连的一条边进行滑动。如果我们滑动了一条边,那不能白滑,最后肯定是要走它的;把它作为"轨道"给其他的边滑也是不优的。观察发现我们最后走的路径一定只由一条边组成,如果多于一条,我们可以把最小的那条拿出来不断滑动,覆盖路径上所有的其他边,这样一定不劣。枚举最后走的那条边(就算不在1~n的某条简单路径上也可以),想办法把它的两个端点分别滑到1和n。有两种滑法:
- 两个点分别通过最短路滑到1和n。当前被枚举的这条边只会被两条最短路覆盖最多一次,先滑最短路覆盖了这条边的那个端点即可。
- 题目里说了滑动过程中是允许自环的,所以我们可以先把两个端点的其中一个滑动到某个位置x,再把另一个用1次操作通过被枚举的边本身滑到x(形成自环),然后两个端点分道扬镳,各自通过最短路滑到1或n。
注意这里的最短路指的是边权为1的最短路,可以用floyd求出。
时间复杂度\(O(n^3)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <LL,LL>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
using namespace std;
LL t,n,m,f[510][510];
vector <pair <pii,LL> > e;
int main()
{
cin>>t;
rep(tn,t)
{
scanf("%lld%lld",&n,&m);
rep(i,n+3) rep(j,n+3) f[i][j]=1e9;
repn(i,n) f[i][i]=0;
e.clear();
LL x,y,z;
rep(i,m)
{
scanf("%lld%lld%lld",&x,&y,&z);
e.pb(mpr(mpr(x,y),z));
f[x][y]=f[y][x]=1;
}
repn(k,n) repn(i,n) repn(j,n) f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
LL ans=1e18;
rep(i,m)
{
ans=min(ans,e[i].se*min(f[e[i].fi.fi][1]+f[e[i].fi.se][n]+1,f[e[i].fi.se][1]+f[e[i].fi.fi][n]+1));
LL u=e[i].fi.fi,v=e[i].fi.se;
repn(j,n)
{
LL val=f[u][j]+1;
val+=f[j][1]+f[j][n]+1;
ans=min(ans,e[i].se*val);
val=f[v][j]+1;
val+=f[j][1]+f[j][n]+1;
ans=min(ans,e[i].se*val);
}
}
printf("%lld\n",ans);
}
return 0;
}
E. Ela Goes Hiking
就差1分钟调完,改了两个字符就过了
比赛公告评论里说是从noip.ac偷的(也可能只是撞了)
考虑求出每只蚂蚁赢的方案数,最后除以总方案数得到概率。n=1的特判。
对于某一种方向选择的状态,先把蚂蚁分段:

一开始,最左和最右(如果存在)两段中的蚂蚁都会合成一个大小\(\geq 1\)的蚂蚁;中间的每一段,从左往右数第一个向左走的蚂蚁会吃掉这一段中所有向右走的蚂蚁,并且继续向左。
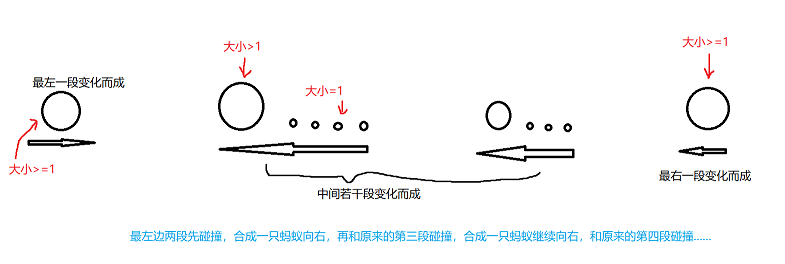
如果最初处在最右边一段的蚂蚁想赢,那它一定是整个序列中最靠右的蚂蚁,并且最靠右一段的长度不小于n的一半。用等比数列求和求出方案数。
如果中间某一段的蚂蚁想赢,那他一定是这一段中从左往右数第一个向左的蚂蚁。这一段中向右的蚂蚁个数要足够多,保证他不被左边所有蚂蚁构成的一只大蚂蚁吃掉。也是等比数列求和计算。现在这只蚂蚁已经和它左边的所有蚂蚁合体,要去吃这一段中剩下向左走的蚂蚁,以及右边其他段中的蚂蚁。为了计算它右边蚂蚁的方案数,我们可以计算出一个数组\(win_i\),表示合理选择最后i只蚂蚁的方向,使得如果前n-i只蚂蚁合体向右推,能够吃穿全场的方案数。转移这里不讲了,只要时刻保证当前蚂蚁团大小不\(\geq\)前面蚂蚁个数之和即可。可以用前缀和优化转移做到\(O(n)\)(需要一个额外的dp数组,因为每一个中间段都分前后两段,所以一共是两个dp数组和两个前缀和数组)。
如果最左边一段的蚂蚁想赢,那最左边一段的蚂蚁数量一定>1,且赢的一定是序列中第2只蚂蚁。用上面的win数组计算答案即可。
时间复杂度\(O(n)\)。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
using namespace std;
const LL MOD=1e9+7;
LL qpow(LL x,LL a)
{
LL res=x,ret=1;
while(a>0)
{
if((a&1)==1) ret=ret*res%MOD;
a>>=1;
res=res*res%MOD;
}
return ret;
}
LL t,n,ans[1000010],win[1000010],add[1000010],mid[1000010],midadd[1000010],wsum[1000010],inv2=qpow(2,MOD-2);
int main()
{
cin>>t;
rep(tn,t)
{
cin>>n;
if(n==1)
{
puts("1");
continue;
}
rep(i,n+3) win[i]=add[i]=mid[i]=midadd[i]=0;
++add[0];add[(n-1)/2+1]=MOD-1;
LL totadd=0,totmadd=0;
rep(i,n)
{
(totadd+=add[i])%=MOD;
win[i]=totadd;
//win->mid
(midadd[i]+=win[i])%=MOD;
(totmadd+=midadd[i])%=MOD;
mid[i]=totmadd;
//mid->win
LL lim=(n-i-1)/2;
if(lim>=2)
{
(add[i+2]+=mid[i])%=MOD;
(add[i+lim+1]+=MOD-mid[i])%=MOD;
}
}
rep(i,n+3) ans[i]=0;
wsum[0]=win[0];
repn(i,n) wsum[i]=(wsum[i-1]+win[i])%MOD;
//第一段
ans[1]=wsum[n-2];
//rep(i,4) cout<<win[i]<<'p';cout<<endl;
//中间
repn(i,n-1)
{
LL mng=max(1LL,(LL)i/2),mxg=i-1,val=1;
if(mng<=mxg)
{
LL av=(qpow(2,i-mng)-qpow(2,i-mxg-1)+MOD)%MOD;
(val+=av)%=MOD;
}
(ans[i]+=val*wsum[n-i-1])%=MOD;
}
//最后一段
LL mng=(n-1)/2,mxg=n-2,val=1;
if(mng<=mxg)
{
LL av=(qpow(2,n-1-mng)-qpow(2,n-1-mxg-1)+MOD)%MOD;
(val+=av)%=MOD;
}
(ans[n-1]+=val)%=MOD;
//rep(i,n) cout<<ans[i]<<' ';cout<<endl;
LL tot=qpow(2,n);tot=qpow(tot,MOD-2);
rep(i,n)
{
(ans[i]*=tot)%=MOD;
printf("%lld\n",ans[i]);
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号