香港中文大学(深圳) DDA2001 - Introduction to Data Science 笔记

PDF下载链接

笔记包括2025年春学期该课程的内容
所有知识点截图均来自李爽教授的课件

期中前

  • Multinomial Logit Model 多项逻辑模型

    \(P_i(S)=\frac{a_i}{1+\sum_{j\in S}a_j}\)

  • 注意看第一份课件最后三页

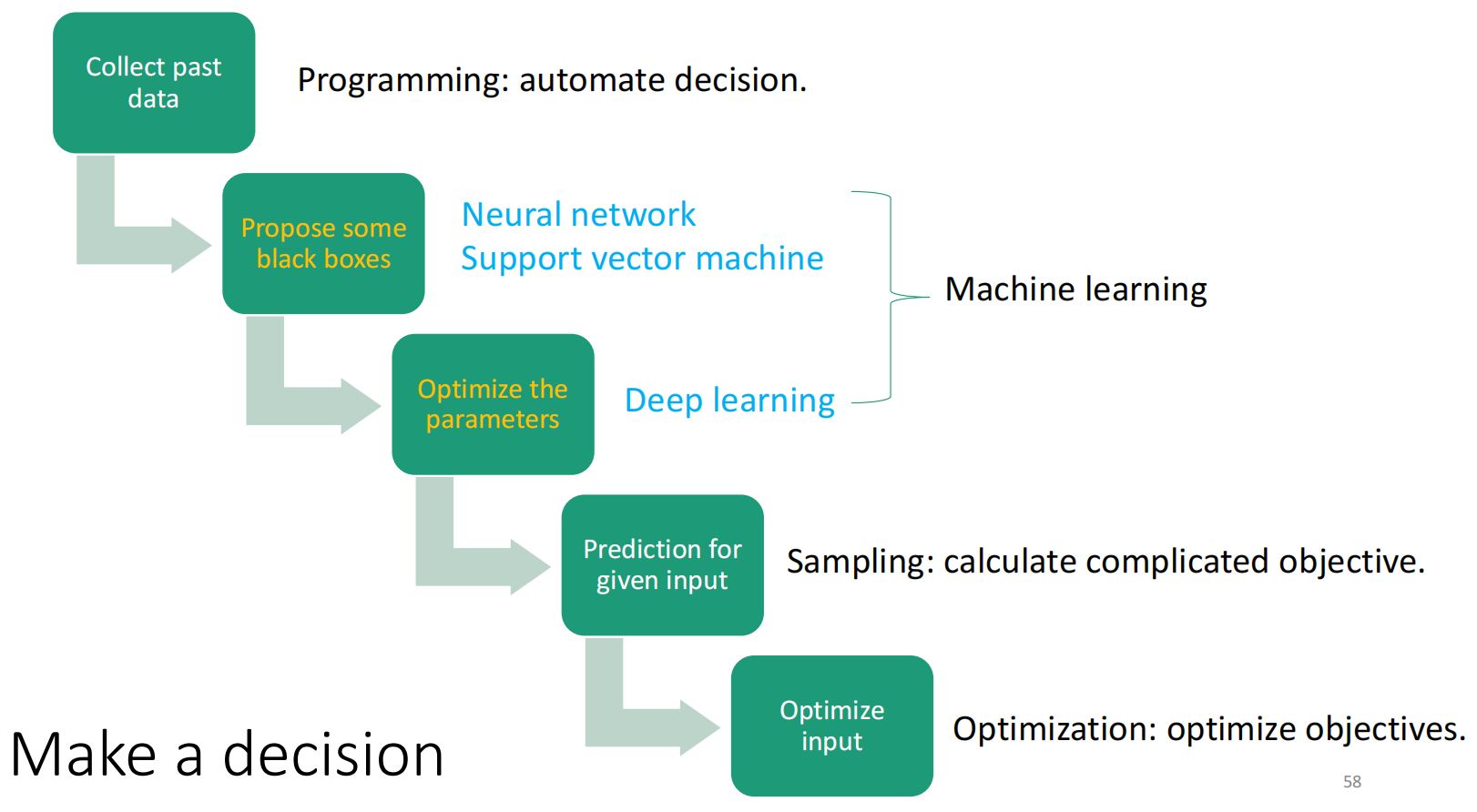
    image-20250223135611224

  • Random Experiment 随机实验：以相同方式进行，但仍然可能产生不同结果的实验

    Sample Space (\(\Omega\)): 所有可能结果的集合

  • 如果事件A和B不包含任何共同结果，那么\(P(A\cup B)=P(A)+P(B)\)

  • 样本空间可能是离散(有限个或无限且可列个结果，也就是可数)或连续(不可数)的

    不可数\(\Leftrightarrow\)集合中的元素无法与自然数建立一一对应关系

  • 补集可以用右上角加一撇来表示，如\(A'\)

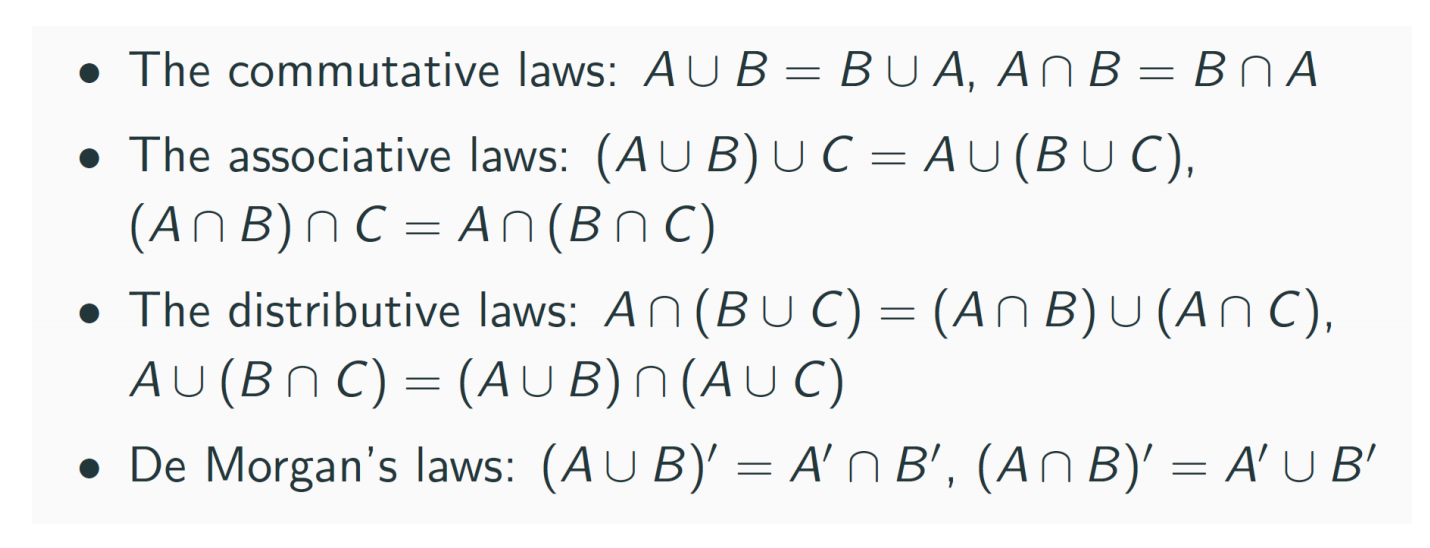
  • image-20250223151441538

  • 两事件独立：\(P(AB)=P(A)P(B)\)

    两事件互斥：\(P(A+B)=P(A)+P(B)\)

  • Probability Mass Function 概率质量函数

    image-20250223152833222

  • Cumulative Distribution Function 累积分布函数

    \(F(x)=P(X\leq x)=\sum_{x_i<X}f(x_i)\)

  • Mean 均值 \(E(x)=\sum xf(x)\)

  • Variance 方差 \(Var(x)=\sum (x-E(x))^2f(x)\)

  • Random Variable 随机变量

    例子：掷骰子，点数\(\geq3\)赚两块钱，否则亏一块钱，则有：

    \(\omega\in S,S=\{1,2,3,4,5,6\}\)

    \(X(\omega)\in R,R=\{1,2\}\)

    随机变量也有概率质量函数和累积分布函数，定义同上

  • \(Var(X)=E(X^2)-(E(X))^2\)

  • Bernoulli Distribution: 取1的概率为p，取0的概率为1-p

  • Binomial Distribution 二项分布: n次Bernoulli Distribution

    随机变量X表示成功的次数

    \(E(X)=np,\ Var(X)=np(1-p)\)

    \(Pr(X=k)=\binom{n}{k}p^k(1-p)^{n-k}\)

    缩写Pr和P都可以用来表示概率，Pr更专业一些

  • Geometric Distribution 几何分布: 不断进行Bernoulli Distribution直到第一次成功

    随机变量X表示做的实验的总次数

    \(E(X)=\frac 1p,\ Var(X)=\frac{1-p}{p^2}\)

    \(Pr(X=k)=(1-p)^{k-1}p\)

  • 关于连续(Continuous)概率分布

    image-20250225152942126

  • Probability Density Function 概率密度函数

    • \(f(\omega)>0,if\ \omega\in S\)
    • \(f(\omega)=0,if\ \omega\notin S\)
    • \(\int_{-\infty}^{\infty}f(x)dx=1\)
    • \(P(a\leq X\leq b)=\int_a^bf(x)dx\)
    • \(f(x)\)越大说明x周围的值越容易被取到
    • 这是否在\(f(x)\)连续时才成立？

  • 连续随机变量的Cumulative Distribution Function

    \(F(x)=\int_{-\infty}^xf(u)du\)

  • 连续随机变量的均值和方差

    \(E(X)=\int_{-\infty}^{\infty}xf(x)dx,\ Var(X)=\int_{-\infty}^{\infty}(x-E(x))^2f(x)dx\)

    \(E(g(X))=\int_{-\infty}^{\infty}g(x)f(x)dx\)

  • Uniform Distribution 均匀分布：指随机变量在某个区间内的每个值具有相等的概率密度

    • 对定积分的估计

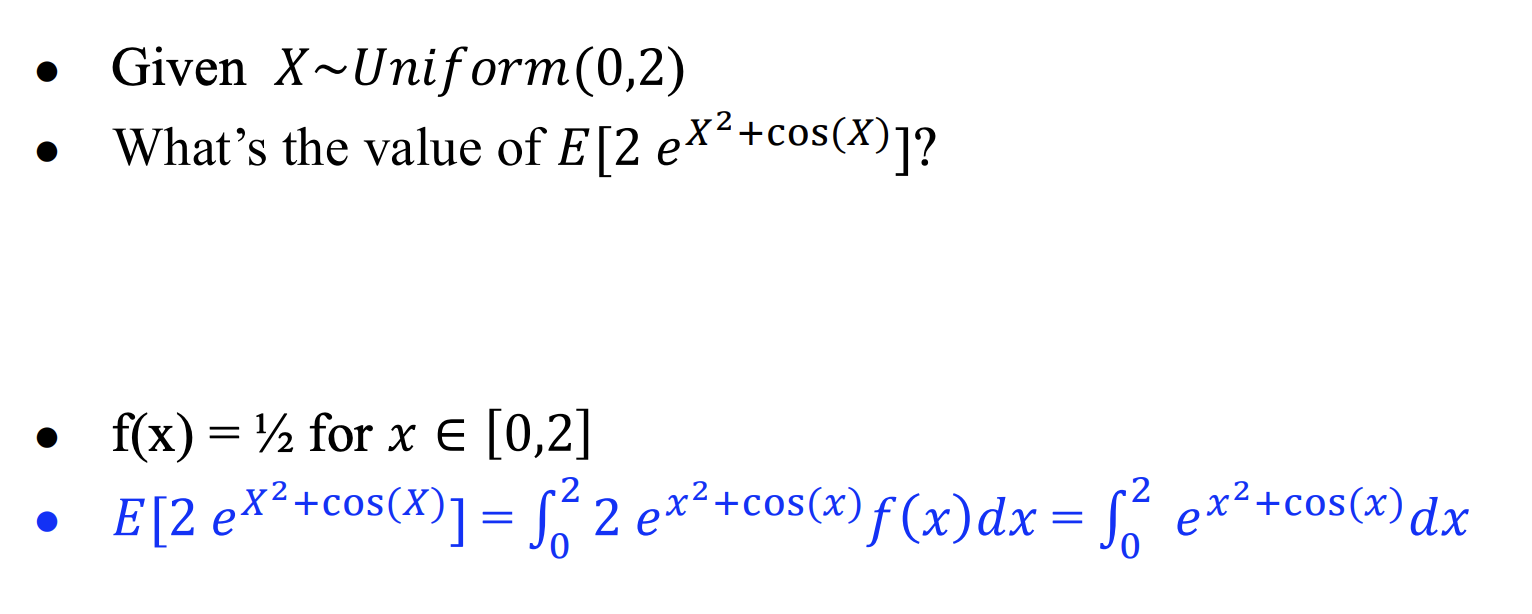
      image-20250225154622318
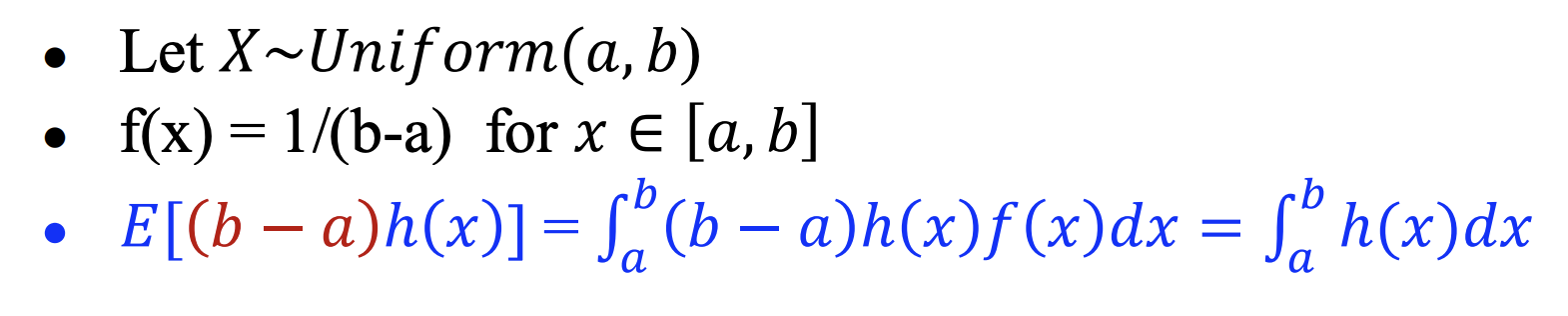
      image-20250225155248245
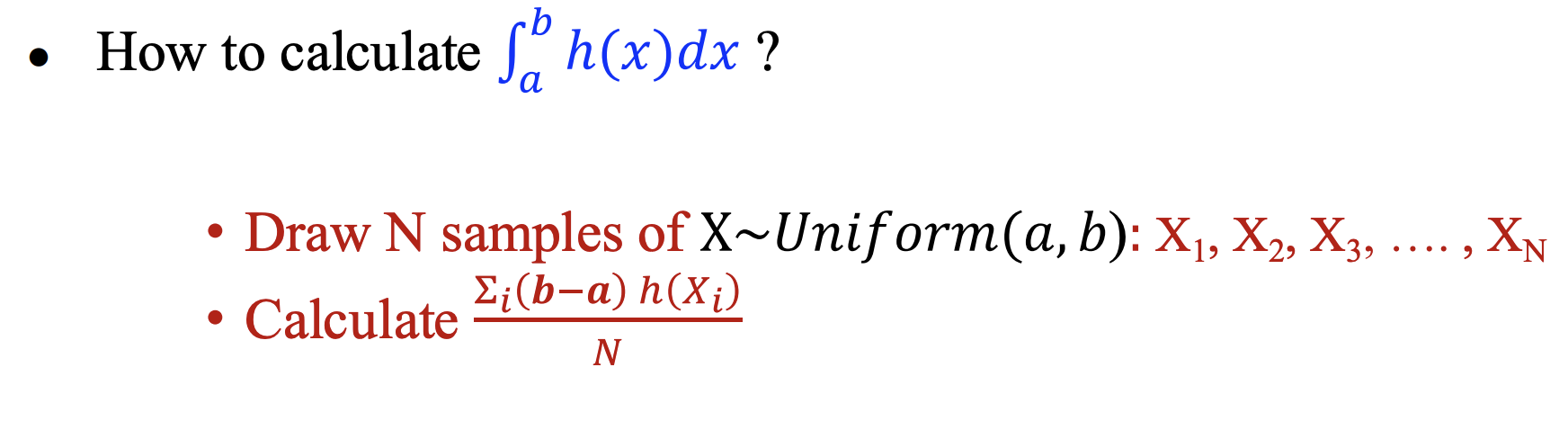
      image-20250225155350532

    • 对其他东西的估计

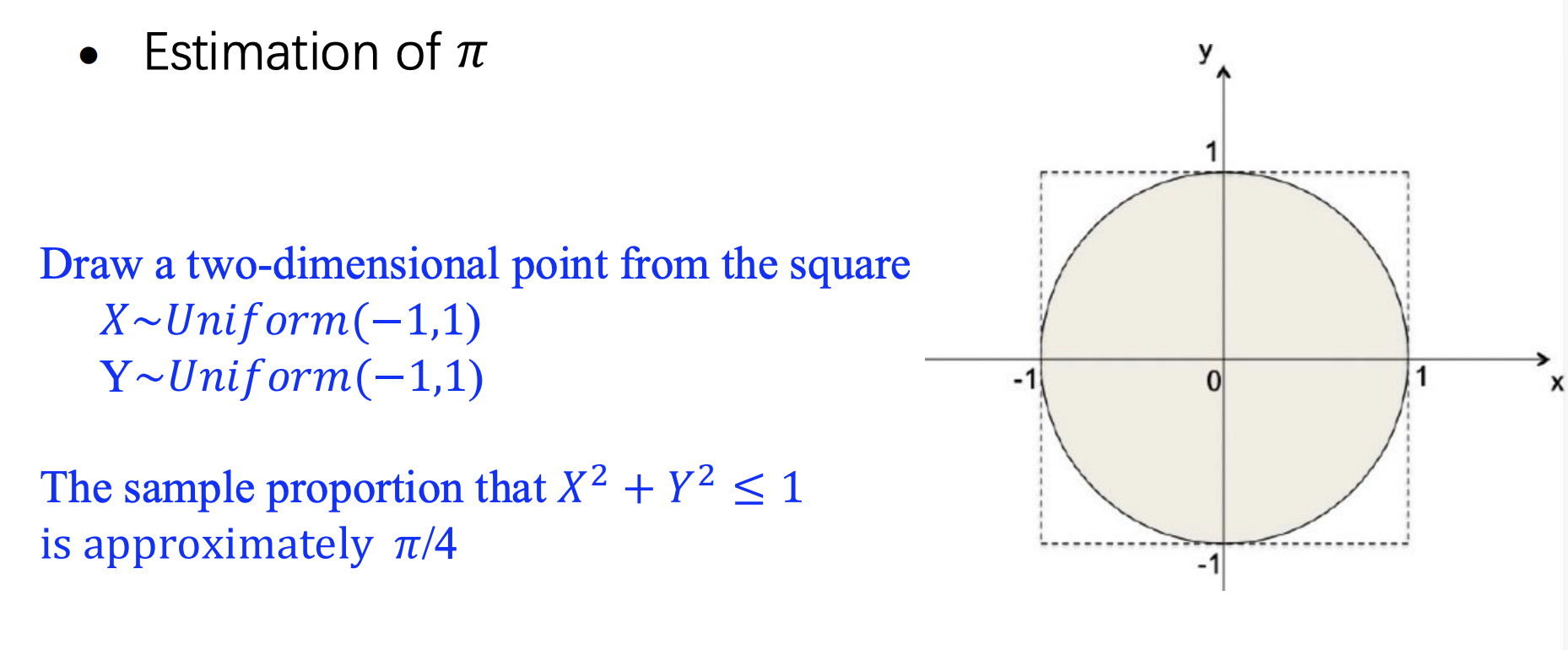
      image-20250225160204232

    • 在估计最后一步取样之前可能需要说by Lindeberg-Lévy CLT

      image-20250225162535924

    • 例：

      image-20250314214916393

  • Normal Distribution 正态分布

    \(f(x;\mu,\sigma)=\frac1{\sigma\sqrt{2\pi}}exp(-\frac{(x-\mu)^2}{2\sigma^2})\)

    其中\(\mu\)是分布的中心，\(\sigma\)越大分布越扁平

    \(E(X)=\mu,\ Var(X)=\sigma^2\)

  • Joint Distribution 联合分布

    是涉及两个及以上变量的分布

    \(f(x,y)=P(X=x,Y=y)\)

    \(\sum_{x,y}f(x,y)=1\)

    \(\sum_yf(x,y)=P(X=x)\)

    • Correlation 两个随机变量之间的相关性(\(\in[-1,1]\))

      image-20250225164403377

      相关性用\(\rho\)表示

      \(\rho(x,y)=\frac{Cov(X,Y)}{\sqrt{Var(X)}\sqrt{Var(Y)}}\)

      其中Cov是Covariance协方差，\(Cov(X,Y)=E[(X-E(X)(Y-E(Y))]=E(XY)-E(X)E(Y)\)

  • Conditional Probability 条件概率

    若\(P(B)>0\)，\(P(A|B)=\frac{P(A\cap B)}{P(B)}\)

  • Maximum Likelihood Estimate 最大似然估计：根据观测数据推断出统计模型中未知参数的值

    选择参数时，一般选择能使实验结果发生的可能性的自然对数最大的那个参数

    选择的参数使实验结果发生的可能性称为likelihood，如果是离散随机变量，\(L(\theta)=P(X_1,X_2\cdots X_n|\theta)\)；如果是连续随机变量的话把概率密度函数PDF乘起来

    log-likelihood: \(l(\theta)=ln(L(\theta))\)

    例：

    image-20250301211153707

  • Regression Analysis 回归分析

    • 线性回归分析

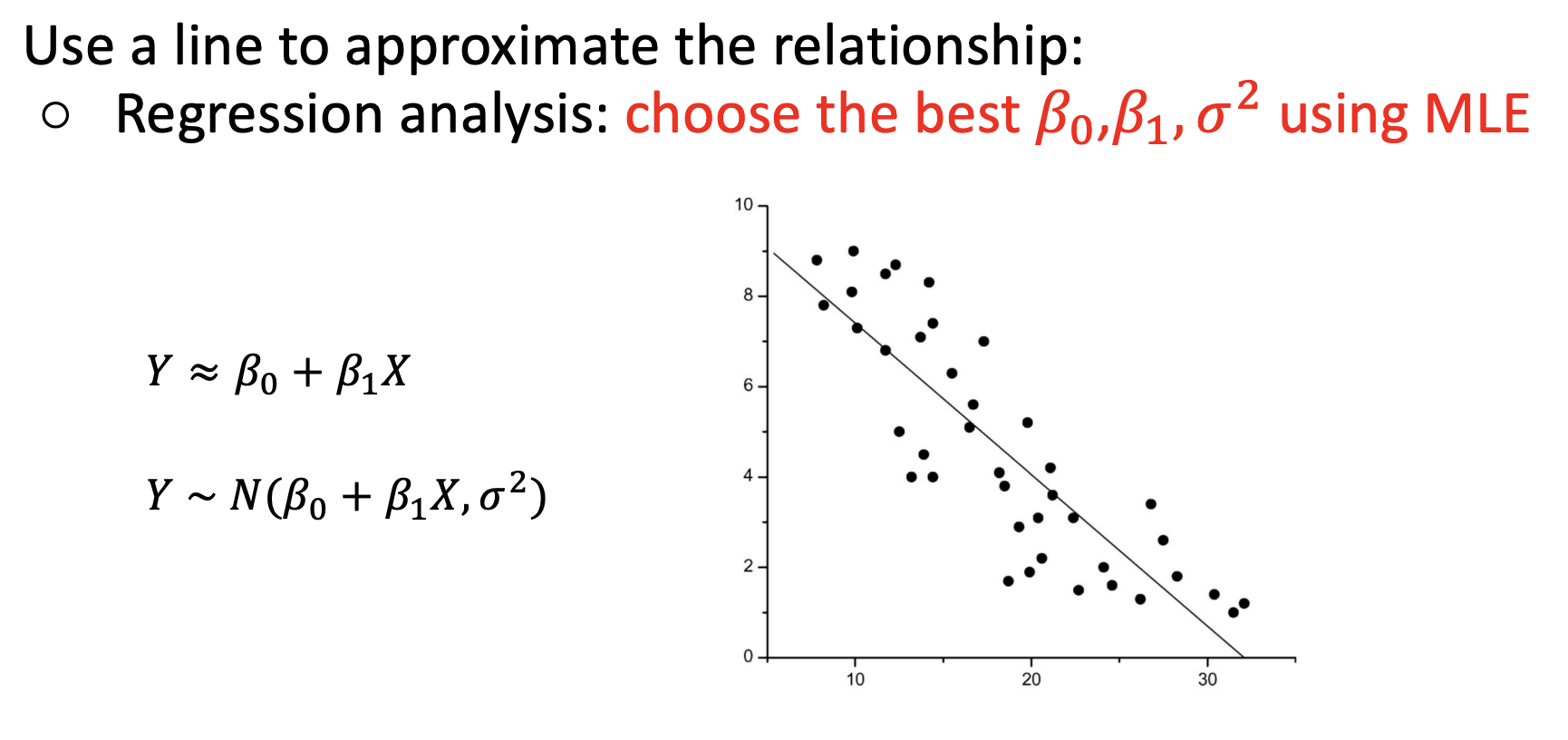
      image-20250301213713928 image-20250301213736491 image-20250301214635787

      以上过程中，要求式子对\(\beta_0,\beta_1\)求偏导之后的结果都为0

      检查线性回归的合理性：xy之间关系是否线性；对不同的x，y的方差是否相等

  • Central Limit Theorem 中心极限定理

    令任意分布的随机变量\(X\)的样本\(X_1\cdots X_n\)；\(X\)的(不是样本的)均值为\(\mu\)，方差为\(\sigma^2\)，则\(n\)足够大时，有\(\overline X\)~\(N(\mu,\frac{\sigma^2}n)\)，也就是\(\frac{\sqrt n(\overline X-\mu)}{\sigma}\)~\(N(0,1)\)

    image-20250225162237392

  • Confidence Interval 置信区间

    例：对某个随机变量(已知其方差为\(\sigma^2\))的均值\(\mu\)的置信区间的估计(根据中心极限定理)：

    image-20250305140905839

    可能性确定的情况下区间的选择：

    image-20250305142708247 image-20250305142718435 image-20250305142735634

    约定：\(z_{\frac{\alpha}2}\)表示\(N(0,1)\)中，\(z_{\frac{\alpha}2}\)右侧的面积为\(\frac{\alpha}2\)

    则这个估计的结果为：

    image-20250305143049597

    其中\(1-\alpha\)被称为confidence level

    估计出的区间长度随几个给定参数的变化：

    • 样本大小\(n\)增加，区间长度减少
    • 样本方差\(\sigma^2\)增加，区间长度增加
    • confidence level \(1-\alpha\)增加，区间长度增加

    例2：

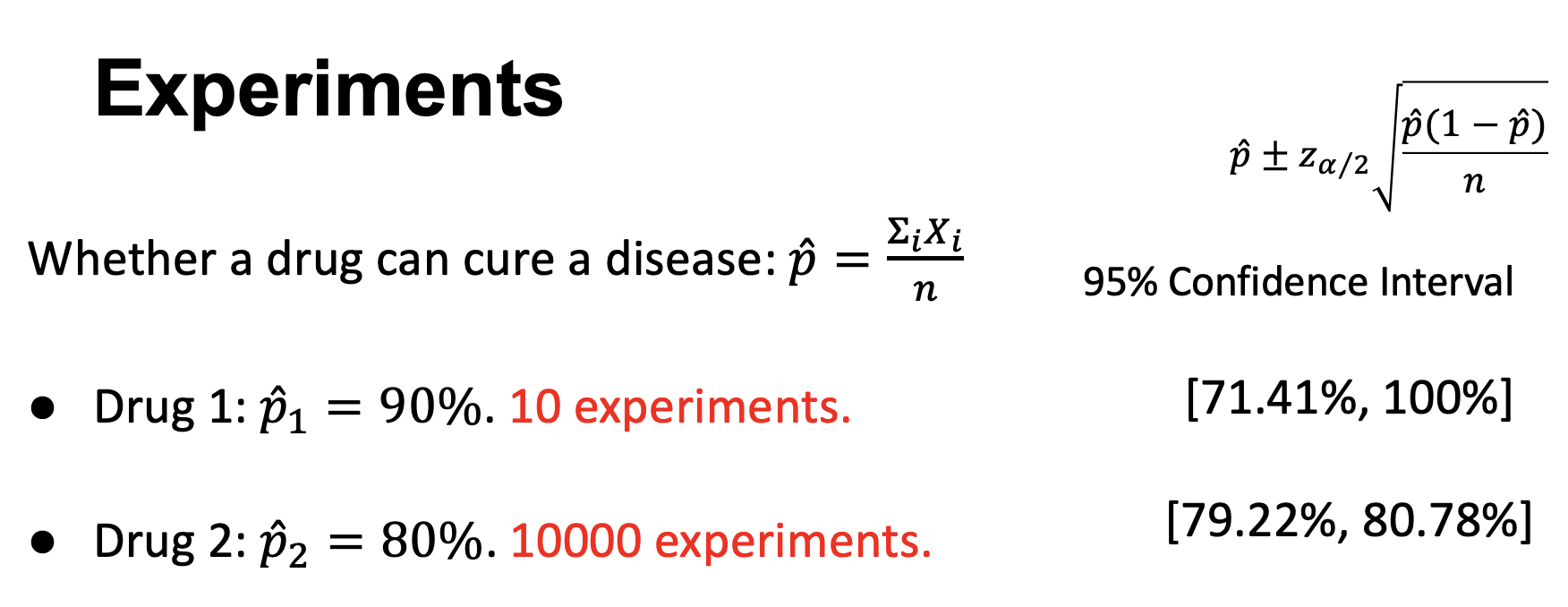
    image-20250305144412967 image-20250305144423475 image-20250305144446407

期中后

  • Optimization

    存在映射\(f:A\to B\in\mathbb R\)，最优化指的是找到\(x_0\ s.t.\ f(x_0)\leq或\geq f(x)\forall x\in A\)

    • 鞍点：指的是\(f\)相对于自变量每个分量在此处的变化趋势都为0的点

    • Convex Set 凸集：集合内任意两点之间连线都在集合内的集合

      证明一个集合是凸集的方法：\(\forall x,y\in S,\theta\in[0,1]\)，有\(\theta x+(1-\theta)y\in S\)

      Theorems & Properties

      • 两个凸集的交是凸集
      • 一个凸函数的上图(Epigraph)是凸集

    • Convex Function 凸函数("向下凸")：定义域是一个凸集，并且\(\forall x_1,x_2\in dom(f),\lambda\in[0,1],有f(\lambda x_1+(1-\lambda )x_2)\leq\lambda f(x_1)+(1-\lambda)f(x_2)\)的函数；在单自变量函数中，充要条件为\(f''(x)\geq0\)；多自变量时，则需要在任意方向的二阶导\(\geq 0\)

      凸函数的局部最小值是全局最小值

    • Concave Function 凹函数("向上凸")：与凸函数恰好相反

      凹函数的局部最大值是全局最大值

    • Epigraph 上图：一个函数图像及其上方所有点组成的集合

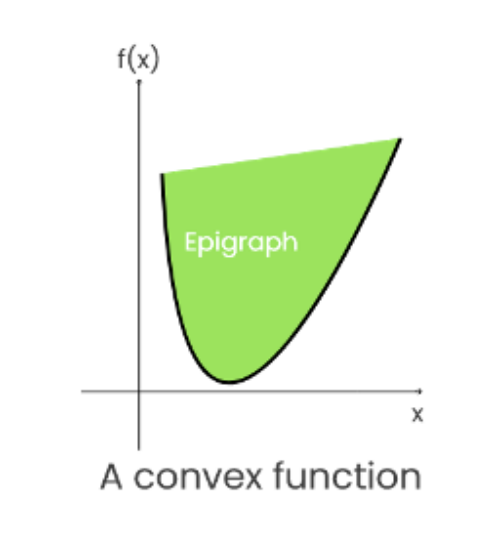
      image-20250403164703082

      一个函数是凸的当且仅当其上图是一个凸集

    • Halfspace 半空间

      高维空间中，通过一个超平面将其分为两部分，每一部分都是一个半空间，如\(a^Tx\leq b\)，所有这样的\(x\)就组成一个半空间

      若干个半空间的交集是凸集

    • 凸函数在经过以下操作后，凸性仍然得以保持

      1. 若干凸函数求和，且其中每一个的系数都非负

        \(f(x)=\sum_{i=1}^n w_if_i(x),w_i\geq 0\)，\(f(x)\)凸

      2. Affine Transformation 仿射变换(缩放和平移)

        \(g(x)=ax+b\)称为一个仿射函数，这里的\(x\)可以是向量，\(a\)可以是矩阵

        若\(f\)是凸函数，\(g\)是仿射函数，则\(f(g(x))\)是凸的

      3. Pointwise Maximum 逐点最大值(新函数的值为若干凸函数的最大值)

        \(f(x)=max\{f_1(x)\cdots f_m(x)\}\)，\(f(x)\)凸

    • 关于凸性的例题

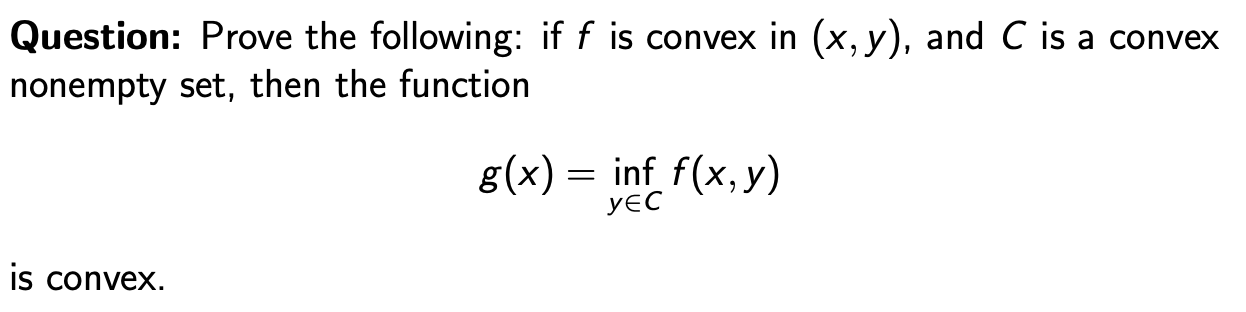
      • image-20250409180156361

        其中inf表示下界，即最小值

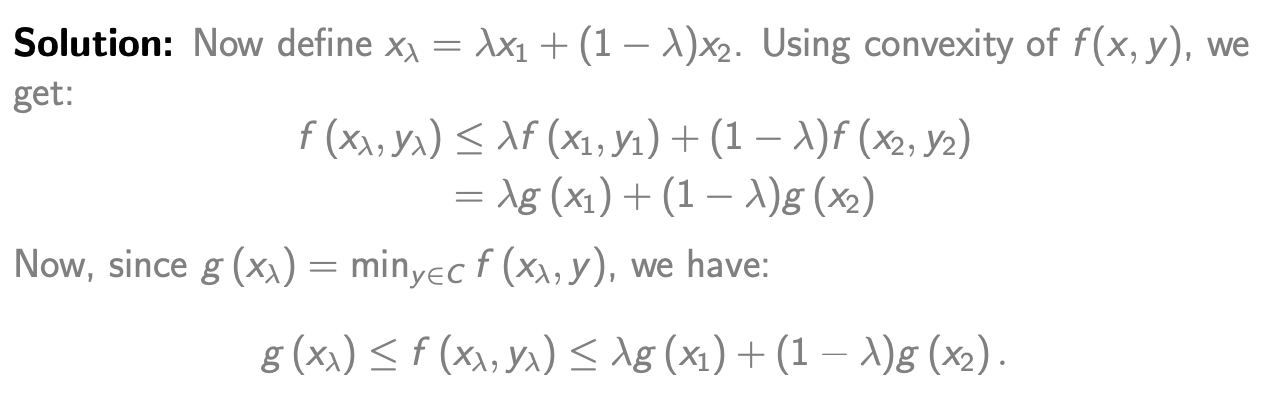
        image-20250409180207641 image-20250409180227363
      • image-20250409180639940

        Solution:

        \(\forall i\in[1,n]\)，令\(g_i(x)=|x_i|\)，易知\(g_i(x)\)为凸函数

        \(\forall a=\{i_1\cdots i_r\}\)，令\(h_a(x)=\sum_{j=1}^rg_{i_j}(x)\)，则\(h_a(x)\)也为凸函数(由上"凸性仍然得以保持"性质第一条)

        \(f(x)=max_{a}\{h_a(x)\}\)，则\(f(x)\)也为凸函数(由上"凸性仍然得以保持"性质第三条)

  • Machine Learning 机器学习

    • 机器学习的过程

      1. Prepare the Training Data
      2. Select and Apply an Algorithm
      3. Train the Model
      4. Deployment and Model Improvement

    • 分类模型和回归模型

      • 分类(Classification)模型输出离散的类别标签，如预测一张图片是猫还是狗
      • 回归(Regression)模型输出连续的数值，如预测一辆汽车的售价

    • 过拟合和欠拟合

      • 模型对训练数据表现极佳但对实际测试数据表现很差，实际上模型是在"记忆"训练数据但没有真正理解它们；像是一个只会背教科书的人，对课本知识了解良好但一考试就原地爆炸。这种情况称为过拟合(Overfit)
      • 模型对训练数据和实际测试数据表现都很差。这种情况称为欠拟合(Underfit)
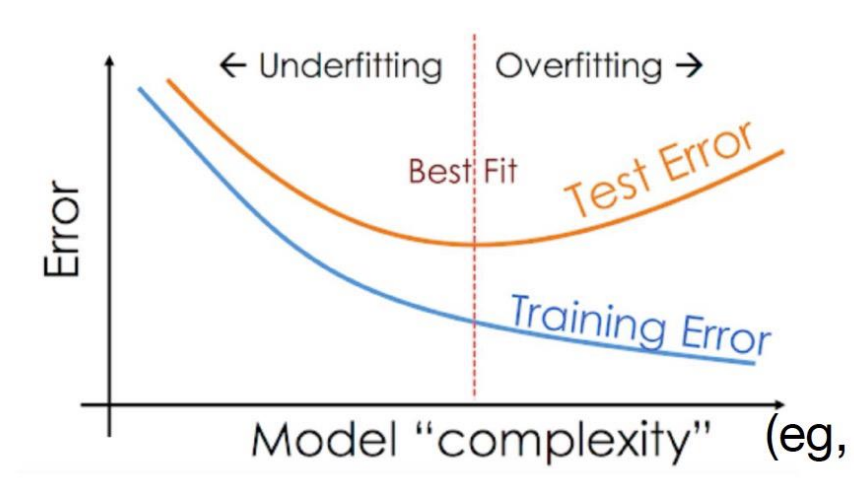
      image-20250506233717829

    • 监督学习和无监督学习

      • 监督(Supervised)学习：给出每组训练数据和其标签，比如给出一些图片，并告诉模型“这是猫，那是狗”，是有明确的标签来指导模型的学习过程(目标："Learn to predict")

        监督学习模型有参数模型(Parametric Model)和非参数模型(Non-parametric Model)的区别，参数模型中默认数据和标签之间的映射关系能够用一个确定的数学形式来描述，这个数学形式由一组有限的参数定义；非参数模型则相反

      • 无监督(Unsupervised)学习：只给出训练数据，比如只给出猫狗的图片让模型尝试自己将其分组，是让模型自己发现数据中的结构和模式(目标："Find patterns")

    • 监督学习算法示例

      • K-Nearest Neighbors

        一次性给出若干训练点的位置和类别，之后会给出一些询问点，要求给这些询问点分类。对于每个询问，找出训练点中距离这个点最近的\(K\)个，并将其分为这\(K\)个点中较多的那类

        K值较小时，容易被数据中的噪点影响，出现过拟合；K值较大时，容易变得平滑，出现欠拟合(意会就行)

        Cross Validation 交叉验证：用于验证哪个K值最合适的方法，过程为在KNN的交叉验证中，数据被划分为\(k\)(这个小\(k\)和大\(K\)没有关系)个子集，通常采用分层抽样以保持类别比例(针对分类问题)。对于每个\(K\)值，循环使用\(k-1\)个子集作为训练集，剩余\(1\)个子集作为验证集，计算预测误差\(\epsilon\)。重复此过程\(k\)次，每次使用不同的子集作为验证集，最后计算平均误差\(\bar{\epsilon} = \frac{1}{k}\sum_{i=1}^{k}\epsilon_i\)来评估模型性能并选择最佳\(K\)值。这种方法确保了模型评估的准确性和可靠性

      • Logistic Regression Logistic回归：

        给出若干组训练数据及其分类(标签)，Logistic Regression可以对每组询问数据，给出其属于每一类的概率

        虽然Logistic回归名字里带回归，输出的结果也是连续的数值，但其本身实现的功能更接近于分类模型

        • Logistic Function (也称Sigmoid Function, S型函数)

          \(\sigma(z)=\frac1{1+e^{-z}}\)

          将任意实数映射到[0,1]中的一个值

        • 执行分类的原理(只有两类的情况)

          \[\begin{align} P(x属于第1类)&=\sigma(\theta^Tx+b)\\ P(x属于第0类)&=1-\sigma(\theta^Tx+b) \end{align} \]

          其中\(\theta\)是由训练数据得出的一个权重向量，\(x\)是由询问数据得出的一个向量，\(b\)是偏差项

          求\(\theta,b\)的方法：MLE，若有\(m\)组训练数据\((x_1\to y_1)\cdots (x_m\to y_m)\)，则有\(l(\theta,b)=\sum_{i=1}^m ln\ P(x_i\to y_i,\theta,b)\)；同时：

          \[\begin{align} &ln\ P(x_i\to y_i,\theta,b)\\ =&-ln(1+exp(-\theta^Tx_i-b))y_i+(1-y_i)(-\theta^Tx_i-b)-\\ &\ ln(1+exp(-\theta^Tx_i-b))(1-y_i)\\ =&(y_i-1)(\theta^Tx_i+b)-ln(1+exp(-\theta^Tx_i-b)) \end{align} \]

          \(ln(1+exp(-\theta^Tx_i-b))\)是凸(Convex)的，证明：

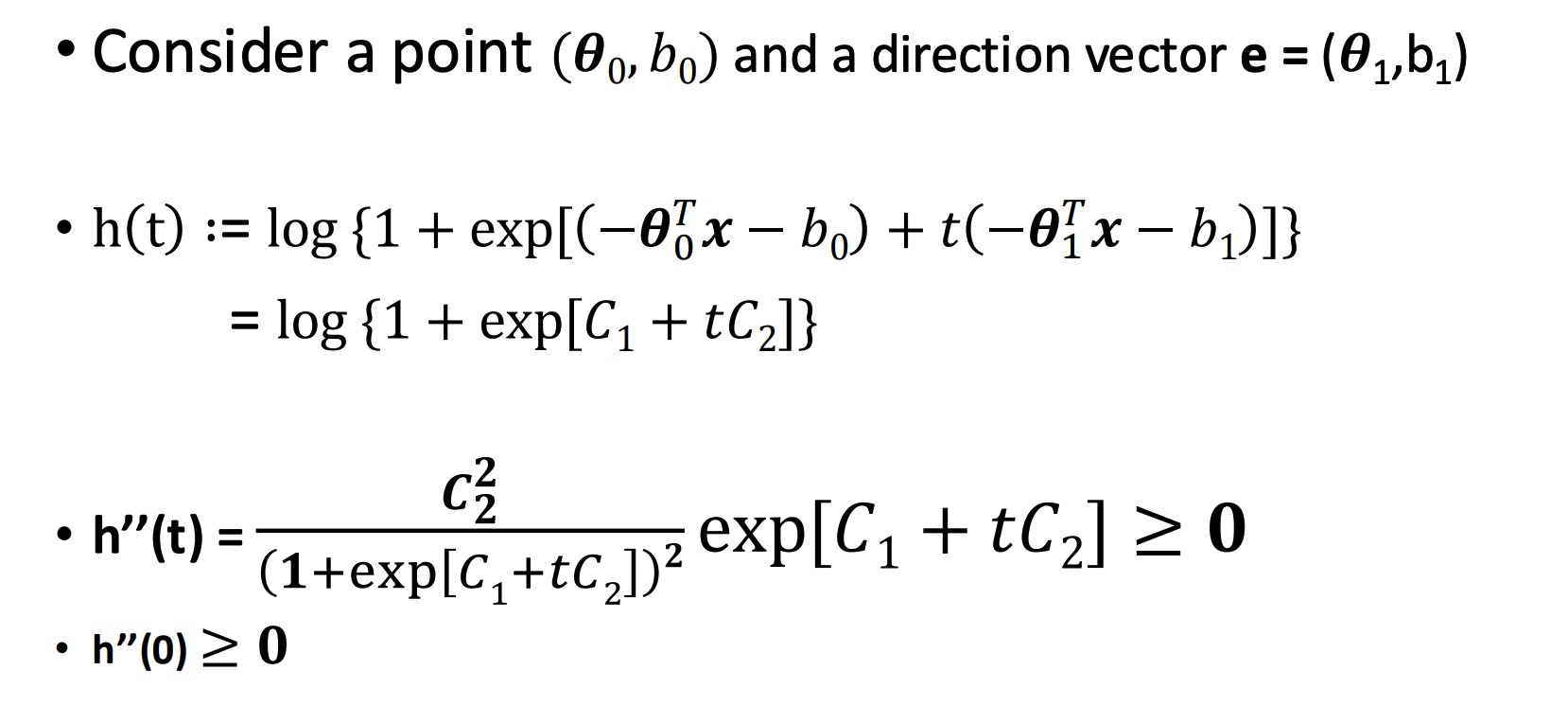
          image-20250419123011852

          因此，\(l(\theta,b)\)是凹(Concave)的

          此时仍然无法直接计算得出\(\theta,b\)。因此使用Gradient Descent法来实现

          流程：

          对于单变量凹函数，在定义域中选择一个起始点\(x_0\)，重复过程\(x_{t+1}=x_t+\alpha_tf'(x_t)\)，其中\(\alpha_t\)是常数，称为Step Size；在\(|x_{t+1}-x_t|\leq\epsilon\)或\(|f'(x_t)|\leq\epsilon\)时我们认为已经找到全局极值点，停止过程。若是凸函数，则将式子中的+改为-

          由于\(l(\theta,b)\)是双变量函数，我们对两个变量分别进行这个过程：

          image-20250419124222029

    • 无监督学习算法示例

      • Clustering 聚类算法：是一大类无监督学习算法的总称

        需要有一个距离函数来衡量两组数据的相似度，再根据这个相似度来进一步聚类：\(d(x,y)\)。该函数必须满足以下条件：

        • \(\forall x,y,d(x,y)=d(y,x)\)
        • \(x=y\Leftrightarrow d(x,y)=0\)
        • \(\forall x,y,z,d(x,y)\leq d(x,z)+d(z,y)\)

        距离越大，相似度越低

        例：

        image-20250508133951923 image-20250508133935444

      • 聚类算法示例：K-means Clustering

        给出\(m\)组数据\(x_1\cdots x_m\)，找出\(k\)个聚类中心\(c_1\cdots c_k\)，并给每组数据分配类别\(\pi_i\)，使\(\sum_{i=1}^md(x_i,c_{\pi_i})\)最小

        当每组数据为高维空间中的一个点(也就是向量)，而\(d(x,y)\)为\(x,y\)之间的欧几里得距离时，K-means Clustering的工作流程如下所示：

        1. 随机取k个聚类中心
        2. 给每个数据点分类，具体来说，将每个数据点分到离其最近的那个聚类中心那一类
        3. 修正聚类中心，具体来说，将每个聚类中心重新设置为所有被分到它这一类的数据点的几何中心(即把每一维坐标都取所有数据点的平均值)
        4. 当所有聚类中心在修正后都不变化(或变化均小于指定的阈值，或迭代次数达到指定的阈值，以防止死循环)时，结束算法；否则，回到第2步

        在第1步中，随机取不同的初始聚类中心可能导致不同的最终分类结果，因为这个算法可能陷入局部最优解

    • 我们想要选出介于过拟合和欠拟合之间的最合适的模型

      选择最合适的模型的方法：验证集法 (Validation Set Approach，一般用于选择监督学习的模型)

      流程：

      1. 将原有的训练数据进一步分为训练数据和测试数据两组
      2. 用训练数据训练若干不同的模型
      3. 用测试数据测试这些模型，选择在测试数据上表现出的误差最小的(由于是监督学习，每组数据都是形如\((x,y)\)，将模型的输出与数据自带的标签\(y\)比较即可得出误差)
      4. 可以将以上流程重复多次，每次在将原有训练数据分组时采用不同的分组策略，以增加模型选择的准确性
posted @ 2025-04-09 21:08  LegendStane  阅读(274)  评论(0)    收藏  举报