CSP 初赛 部分知识整理

几年前整理的东西，要不就发到网上吧
不过现在这些东西里面也有很多考得比以前少了

1. 卡特兰数

   \(f(i)=\sum_\limits{i=0}^{n-1}{f(i)f(n-i-1)}\)

   其中\(f(0)=1\)

   \(f(n)=\)一个凸\(n\)边形用不相交的对角线划分成三角形的方法种数。

   证明：对于一条边，在另外的\(n-2\)个顶点中选一个与这两个顶点连边。若选出的节点在这条边左边的节点顺时针方向\(i\)个，则方法数为 \(f(i-1)f(n-i)\) 。

   具体例子: n个节点的二叉树的个数；1~n 元素的出栈顺序种数；凸多边形划分；平面直角坐标系中从\((0,0)\)移动到\((n,n)\)，只能向右或向上移动一格，且永远不超出\(y=x\)的方法数。

   前几项: \(1, 2, 5, 14, 42, 132, 429\cdots\)

2. 二叉树遍历

   前序遍历：根左右

   中序遍历：左根右

   后序遍历：左右根

3. 哈夫曼编码

   思想：贪心

   \(n\)个字符每个出现\(a_i\)次，每次从优先队列中取出权值最小的两个元素，合并成一个元素，在二叉树上分别连一条边到那两个元素。最后向左的边赋0，向右的边赋1.

4. 完美二叉树\(=\)满二叉树

   完全二叉树\(=\)只有最后一行最右边不满的二叉树

5. 中国计算机学会于1984年创办全国青少年计算机程序设计竞赛。

6. 编程语言分类：

   设计方法：

   • 面向过程：C
   • 面向对象：其他
   • smalltalk：面向对象鼻祖

   执行方式：

   • 编译型：C, C++
   • 解释型：Python, JavaScript\(\cdots\)
   • 混合型：Java, C#\(\cdots\)

7. 图灵奖：美国计算机协会，1966年设立；华人唯一姚期智，2000年获奖

8. 长度为1的线段上随机取两个点期望长度：取中点，讨论，列方程；或建坐标系求体积

9. 抽奖机中有红蓝两色的球，抽到蓝球就继续······设抽到第一个红球之前抽到蓝球的期望个数\(x\),则\(x=\frac{1}{2}\times0+\frac{1}{2}\times(1+x)\), \(x=1\)

10. TCP/IP四层模型：应用层，传输层，网络层，数据链路层

11. 原码：符号位+绝对值

    反码：正数是本身，负数是符号位不变，其他取反

    补码：正数是本身，负数是符号位不变，其他取反+1

12. 十进制小数转二进制：

    0.6 * 2 = 1.2 ——————- 1
    0.2 * 2 = 0.4 ——————- 0
    0.4 * 2 = 0.8 ——————- 0
    0.8 * 2 = 1.6 ——————- 1
    0.6 * 2 = 1.2 ——————- 1

    \(\cdots\)

13. 主定理

    \(T(n)=aT(\frac{n}{b})+f(n)\)

    • \(f(n)\)是n的幂次，\(log_b(a)\)比这个幂次大，\(T(n)=n^{log_b(a)}\)

    • \(f(n)=n^{log_b(a)}\log^k(n)\), \(T(n)=n^{log_b(a)}\log^{k+1}(n)\)

    • \(\cdots\)

14. 稳定的排序方法：冒泡插入 归并基数

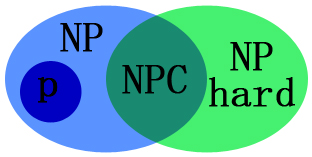
15. P问题：可以在多项式时间内被解决的问题。

    NP问题：可以在多项式时间内被验证的问题。或者说，可以在非确定性多项式时间内被解决的问题。

    NP-Hard问题：如果可以证明某问题有一个子问题是NP-Hard问题，那么该问题是一个NP-Hard问题。

    NP-Complete问题：如果一个问题已经被证明是一个NP-Hard问题，并且可以证明该问题是一个NP问题，那么该问题是NPC问题。