[题解] Codeforces 1268 D Invertation in Tournament 结论，兰道定理

题目

本题需要用到的结论：

一.兰道定理

二.如果\(n\geq4\)，那么\(n\)个点的强连通竞赛图存在\(n-1\)个点的强连通子图。

证明：

现在有一个n-1个点的竞赛图(不一定强连通，称其为原图)，加入n号点，得到的n个点的竞赛图是强连通的。将原图强连通分量分解，按照拓扑序排好，称为\(a_0 \cdots a_k\)(一共k个强连通分量)。现在考虑证明加入n号点后的图，删掉某一个点后一定可以得到强连通图。

1. k=1：去掉n号点即可。

2. \(k \geq 3\)：原图是长成这样的(不太准确，看个大概就行)：
   
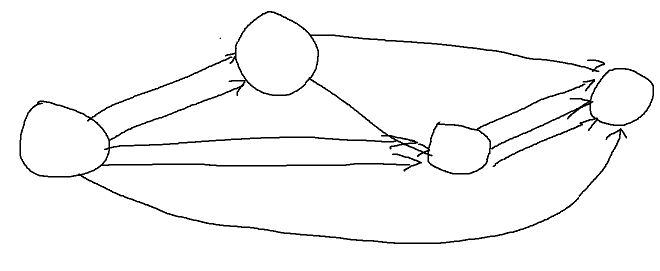
   也就是每两个分量之间都有从前到后的边。现在加入n号点，形成强连通图，既然强连通，那么\(a_k\)到n肯定有边，n到\(a_0\)也肯定有边。可以在任意一个\(a_i(0<i<k)\)中任选一个点删掉，这时任意两个点u和v(\(u,v \neq n\))仍然可以通过\(u \to a_k \to n \to a_0 \to v\)的方式到达。n号点和其他点之间显然可以任意到达。

3. k=2 因为\(n \geq 4\)，所以两个分量里一定有至少一个有>1个元素，我们选择元素>1个的分量，从里面删一个点。以删\(a_1\)中的点为例，在\(a_1\)中随便挑一个到n有边的点r，因为\(a_1\)强连通，所以能够在\(a_1\)中选出一个以r为根的"反向"生成树：
   
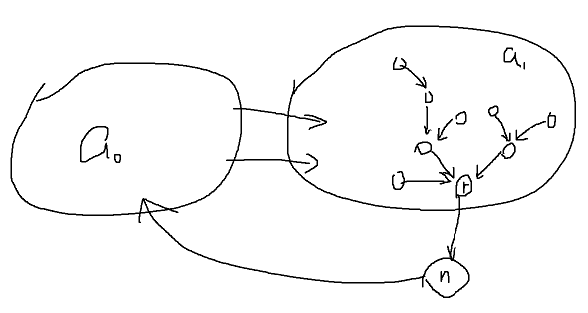
   在这个生成树里任意选一个叶子删掉，可以发现不影响任意两个节点之间的可达性。删除\(a_0\)中的点也是一样证明的，只是生成树变成了正向的。到这里2号结论就证完了。

三. \(n \geq 4\)时，n个点的强连通竞赛图可以翻转一个点，使得操作后的图仍然强连通。
根据结论二，可以先找出n-1个点的强连通子图，把剩下的1个点翻转即可。

四. \(n \geq 7\)时可以翻转至多1个点使图强连通。
证明：
还是像上面的证明一样把scc的拓扑序列出来

1. k=1 不需翻转直接合法
2. \(k \geq 3\)，任选一个i满足\(0<i<k\)，翻转\(a_i\)中的一个点x，发现任意u,v(\(u,v \neq x\))都有路径\(u \to a_k \to x \to a_0 \to v\)；x和其他节点之间显然也是可以互相到达的。
3. k=2 \(a_0和a_1\)必有一个分量大小\(\geq 4\)，假设\(a_1\)大小\(\geq 4\)，根据结论三，在里面可以翻转一个点，使得\(a_1\)仍然强连通，且整个图产生环，变为强连通图。

---

有了这些结论这题就基本做完了，\(n\leq 6\)的暴力枚举翻转的点集，其余情况枚举翻转哪一个节点或者是不翻转，检查的时候直接用兰道定理就可以了。
时间复杂度\(O(n^2log_2n)\)。

点击查看代码

#include <bits/stdc++.h>

#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define pb push_back
#define fi first
#define se second
#define mpr make_pair

using namespace std;

int n,D[2010];
string s[2010];
char c[2010];

bool check(vector <int> v)
{
  sort(v.begin(),v.end());
  int sum=0;
  rep(i,v.size()-1)
  {
    sum+=v[i];
    if(sum==i*(i+1)/2) return false;
  }
  return true;
}

bool isGood(int msk)
{
  int d[10],sw[10];
  rep(i,10) d[i]=0;
  rep(i,n) sw[i]=((msk&(1<<i))>0 ? 1:0);
  rep(i,n) rep(j,i)
  {
    int dir=(s[i][j]-'0')^sw[i]^sw[j];
    if(dir==1) ++d[j];
    else ++d[i];
  }
  vector <int> v;rep(i,n) v.pb(d[i]);
  return check(v);
}

bool isGood2(int id)
{
  int d[2010];
  rep(i,n) d[i]=D[i];
  if(id>-1)
  {
    rep(i,n) if(i!=id)
    {
      int dir=(s[id][i]-'0')^1;
      if(dir==1) ++d[i],--d[id];
      else --d[i],++d[id];
    }
  }
  vector <int> v;rep(i,n) v.pb(d[i]);
  return check(v);
}

int main()
{
  freopen("rv.in","r",stdin);
  freopen("rv.out","w",stdout);
  cin>>n;
  rep(i,n)
  {
    scanf("%s",c);
    s[i]=c;
  }
  if(n<=6)
  {
    pii ans=mpr(1e9,0);
    rep(i,1<<n) if(isGood(i))
    {
      int res=__builtin_popcount(i),vv=1;
      repn(j,res) vv*=j;
      if(res<ans.fi) ans=mpr(res,vv);
      else if(res==ans.fi) ans.se+=vv;
    }
    if(ans.se==0) puts("-1");
    else cout<<ans.fi<<' '<<ans.se<<endl;
  }
  else
  {
    rep(i,n) rep(j,i)
    {
      int dir=(s[i][j]-'0');
      if(dir==1) ++D[j];
      else ++D[i];
    }
    if(isGood2(-1)) puts("0 1");
    else
    {
      int ans=0;
      rep(i,n) if(isGood2(i)) ++ans;
      cout<<1<<' '<<ans<<endl;
    }
  }
  return 0;
}