Codeforces Round #628 (Div. 2)
Codeforces Round #628 (Div. 2)
A. EhAb AnD gCd
Problem Restatement
给出一个整数\(x\),请你构造两个整数\(a,b\),使得\(\gcd(a,b)+\text{lcm}(a,b)=x\)。
\((2≤𝑥≤10^9,1\leq a,b,\leq 10^9)\)
Solution
令\(a=1,b=x-1\)即可。
B. CopyCopyCopyCopyCopy
Problem Restatement
给出一个长度为\(n\)的序列\(a\),并构造一个新的序列按顺序包含\(n\)个序列\(a\)。
求出新序列中最长的严格上升子序列。
$(1≤𝑛≤10^5 , 1≤𝑎𝑖≤10^9) $
Solution
设\(a\)序列中有\(m\)个不同的数字的话,它的最长严格上升子序列,最长一定只能是\(m\)。
所以新的序列中,最长的严格上升子序列也就只能是\(m\)。
由于\(m\leq n\),所以新序列中每一个\(a\)按顺序挑出来一个数,那么一定能构造出来一个长度为\(m\)的严格上升子序列。
那么答案就很明显了:排序+去重后的序列,即是答案。
C. Ehab and Path-etic MEXs
Problem Restatement
给你一颗节点数为\(n\)的树,请你将\([0,n-2]\)里的整数作为权值,分配给\(n-2\)条边,使得((对于任意两个节点\(u,v\)的唯一路径,在路径之外的所有边的最小值)中的最大值 )最小。
\((2≤𝑛≤10^5)\)
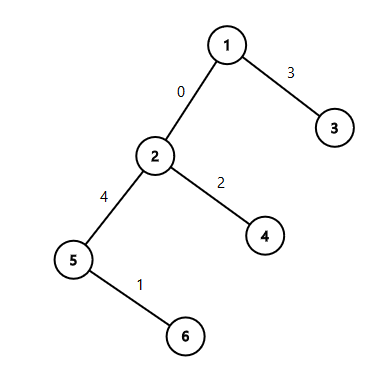
如图,选取任意两个点构成的路径,之外的最小值中最大至少也只能为\(2\)。而这也是最小情况了。
Solution
题目有点绕,但是理解之后不难发现,树上的叶子结点其实是解题的重中之重(由于这是一个无根树,所以叶子结点不妨定义成所有度数为\(1\)的节点)。
因为对于任意一条路径,最多只能占有两个叶子结点,所以对于叶子数大于\(2\)的树来说,无论路径怎么选择,都至少有一个叶子结点暴露在路径外面。那很明显,我们把叶子结点上按顺序放满最小的那些权值,剩下权值随意分配即可。(对于叶子数小于等于\(2\)的树,权值的分配并不影响答案,特判我都懒得写)
当然聪明的你肯定已经发现,其实填\(0,1,2\)就可以了,剩下的其实都没关系,但是这么写方便啊(反正更严格不扣分)
Code
按照我的思路写,代码真的简洁。
#include <bits/stdc++.h>
#define LL long long
#define MAXN 100005
using namespace std;
int f[MAXN],g[MAXN],dgr[MAXN];
void solve(){
int n;
scanf("%d", &n);
memset(dgr+1,0,(n-1)*sizeof(dgr[0]));
for(int i=1;i<n;i++){
scanf("%d %d", &f[i], &g[i]);
dgr[f[i]]++,dgr[g[i]]++;
}
int cnt=0,cntd=n-2;
for(int i=1;i<n;i++){
if(dgr[f[i]]==1 || dgr[g[i]]==1)
printf("%d\n", cnt++);
else
printf("%d\n", cntd--);
}
}
int main(){
int T=1;
// scanf("%d", &T);
while(T--){
solve();
}
return 0;
}
D. Ehab the Xorcist
Problem Restatement
给你两个自然数\(u,v\),请你构造一个最短的正整数序列,使得序列所有元素按位异或为\(u\),所有元素之和为\(v\)。(如果无解输出\(-1\))
\((0≤𝑢,𝑣≤10^{18})\)
Solution
这题很明显是考察按位异或\(\oplus\)的性质。
先判断特殊的情况:
如果\(u>v\),很明显无解,因为按位异或可以理解成进位的加法,不可能比加法结果大。
如果\(u=v=0\),按照样例可以有空序列,所以这个答案为空序列。
如果\(u=v\not=0\),那么答案为长度为\(1\)的序列\(u\)。
如果\(u\)和\(v\)二进制个位不相等(即\(u\)与\(v\)奇偶性不同),也是无解的,因为个位上相加与异或值必须一样(因为前面没有进位)。
考虑完特殊情况,考虑\(\oplus\)的其他特殊性质,比如\(a\oplus a=0,a\oplus 0=a\)。这两个性质可是好性质啊,如果我们能构造一个序列,\(\oplus\)到最后变成\(u\oplus 0\)岂不是美滋滋。按照这个思路,正好我们论证了,\(u,v\)奇偶性相同且\(v> u\)(其余情况已经被特判),不妨让\(x=\frac{v-u}{2}\)。我们有\(u\oplus x\oplus x=u\)且\(u+x+x=v\)。所以我们构造出来了一个通用的三元解\((u,\frac{v-u}{2},\frac{v-u}{2})\)。
那我们只需要考虑二元解是否存在即可。
在比赛现场的时候,由于本人还是对异或不熟悉,导致我直接开写了一个按位构造,代码能力差的我把写的一塌糊涂,导致我花了30多分钟在这题上面,代码还很难看。比赛代码(千万不要点开,写的太丑AAAA)
然而,的确是有更简单的构造方法的。前提是得知道另性质\(a+b=a\oplus b+2*(a\& b)\)。为什么呢,之前我们说了:按位异或可以理解成进位的加法。那么什么时候会进位,那就是所有按位与为\(1\)的时候啦!那么为什么有\(2*\)呢,因为进位之和的值要全体左移一位。就这样,我们推导出了这个公式。
根据这个公式我们发现,\(v=u+2*(a\& b)\),那么\(a\&b=\frac{v-u}{2}=x\)。Wow,这个操作让限制条件从\((u,v)\)转换成了\((u,x)\)。我们不需要判断+中的进位,只需要整整意义上按位来考虑问题。
那么考虑\(\oplus\)和\(\&\)中的每一位来构造二元解,我们会发现只有当\(u\)中某一位为\(1\)的同时\(x\)中某一位也为\(1\)时,是无法构造的。换句话说,如果\(u\&x\)不为\(0\),则无二元解。
而对于有二元解构造结果来说,不妨让一个数为\(u+x\),另一个数为\(x\)即可,即\((u+\frac{v-u}{2},\frac{v-u}{2})\)
#include <bits/stdc++.h>
#define LL long long
using namespace std;
void solve(){
LL u,v;
scanf("%lld %lld", &u, &v);
if(u>v || (v-u)%2==1){
printf("-1\n");
return;
}
if(u==v){
if(u==0) printf("0\n");
else printf("1\n%lld\n", u);
return;
}
LL x=(v-u)/2;
if(u&x)
printf("3\n%lld %lld %lld\n",u,x,x);
else
printf("2\n%lld %lld\n", u+x,x);
}
int main(){
int T=1;
// scanf("%lld", &T);
while(T--){
solve();
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号