CF1304F Animal Observation
F. Animal Observation
Problem Restatement
给出一个\(n\times m\)的自然数矩阵，给定\(k\)。在矩阵的每一行选一个点，作为左上角，放置一个\(2\times k\)的矩阵块（如果是最后一行，则放置\(1\times k\)的矩阵块）。现在要使得，这些矩阵块所覆盖自然数之和最大，求最大值。
$(1≤𝑛≤50,\ 1≤k\leq 𝑚≤2⋅10^4,\ 0\leq a_{ij}\leq 1000) $
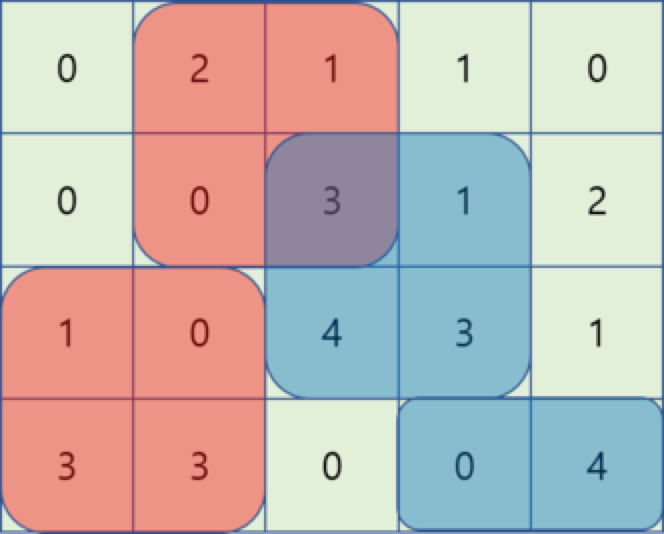
如图便是一个\(4\times 5\)的矩阵，其中\(k=2\)，即\(2\times 2\)的矩阵块（红色和蓝色为矩阵块）为，该放置的所求即为其覆盖的数字之和（重复的只计算一遍）。
Solution
从分治（动态规划）的角度思考，也就是每一行每一列之间的转移。
定义\(dp[i][j]\)为只考虑原矩阵有\(i\times m\)个元素的时候，选择第\(i\)行的第\(j\)个元素作为第\(i\)行的矩阵块左上角元素时，覆盖数之和最大值。
也就是说\(ans=\max(dp[n][j])\)
思考转移方程，我们在每增加一行的同时，我们不但要为上一层选定对应的\(k\)个值，还要为本层选定\(k\)个值，同时过程中我们还要扣除重复(幸运的是，显然本题所有重复都最多被重复一次，而且就在两个相邻行之间)。
那么对于\(dp[i][j]\)来说，肯定是要选择 \(a_{i,j},a_{i,j+1}...a_{i,j+k-1}\)这\(k\)个数字。那么对于这\(k\)个数字中的第\(t\)个，上一行覆盖到的，所有的\(dp[i-1][j+t-k+1]～dp[i-1][j+t]\)之间所有数，都要相应的\(-a_{i,j+t}\)。处理完之后我们再找个最大值，加上去即可。
也就是说\(dp[i][j]=\max(dp_{处理完}[i-1][j])+\sum\limits_{x=j}^{j+k-1}a_{i,x}\)。
但是直接区间处理+区间最值的复杂度很高，每算一个\(dp[i][j]\)，需要\(O(k^2+m)\)的复杂度，总复杂度为\(O(nm(k^2+m))\)，连easy version都过不了。
不过，区间处理？区间最值？我们想到了线段树。如果在算第\(i\)行时，我们先对上一行的\(dp[i-1][j]\)建一个长度为\(m\)的线段树，然后每算一个\(dp[i][j]\)我们对那\(k\)个数进行区间处理\(-a_{i,j+t}\)，然后求最值。我们就把单次复杂度降到了\(O(k\log m)\)，总复杂度为\(O(nmk\log m)\)。对于easy version来说，\((1\leq k\leq20)\)已经可以AC了。
然而我们考虑在第\(i\)行之间动态规划的时候，其实如果你刚算完\(dp[i][j-1]\)，这个时候你会发现，\(dp[i][j]\)覆盖的区域与\(dp[i][j-1]\)覆盖的区域相差只有收尾两个数字，也就是说只需要还原一下开始，处理一下结尾即可，首：\(区间+a_{i,j-1}\)，尾：\(区间-a_{i,j+k-1}\) ，两次区间处理即可。 总复杂度已经\(O(nm\log m)\)，可以AC全题了。
Details
当然实际实现会有一些细节处理。比如：
最开始需要预处理一下前缀和。
我们在建树的时候就直接把前面\(k-1\)个顺便就处理了（这样常数小一点）。
而且我们其实只需要维护\(1～m-k+1\)即可，因为后面那些的选了肯定不如前面。
等等，具体可以看代码。
Code
#include <bits/stdc++.h>
#define MAXN 55
#define MAXM 20005
using namespace std;
struct node{
int le,ri;
int mx,tag;
}sgt[MAXM<<2];
int n,m,k;
int a[MAXN][MAXM],sum[MAXN][MAXM],dp[MAXN][MAXM];
void build(int cur,int l,int r,int x){
sgt[cur].le=l, sgt[cur].ri=r;
sgt[cur].tag=0;
if(l==r-1){
sgt[cur].mx=dp[x-1][l]+sum[x][l+k-1]-sum[x][max(k-1,l-1)];
}
else{
int le=cur<<1,ri=le+1;
build(le,l,(l+r)>>1,x);
build(ri,(l+r)>>1,r,x);
sgt[cur].mx=max(sgt[le].mx,sgt[ri].mx);
}
}
void update(int cur){
int le=cur<<1,ri=le+1;
sgt[le].mx+=sgt[cur].tag;
sgt[ri].mx+=sgt[cur].tag;
sgt[le].tag+=sgt[cur].tag;
sgt[ri].tag+=sgt[cur].tag;
sgt[cur].tag=0;
}
void modify(int cur,int l,int r,int del){
if(l<=sgt[cur].le && sgt[cur].ri<=r){
sgt[cur].mx+=del;
sgt[cur].tag+=del;
}
else{
if(sgt[cur].tag) update(cur);
int le=cur<<1,ri=le+1;
int mid=(sgt[cur].le+sgt[cur].ri)>>1;
if(l<mid) modify(le,l,r,del);
if(r>mid) modify(ri,l,r,del);
sgt[cur].mx=max(sgt[le].mx,sgt[ri].mx);
}
}
void solve(){
scanf("%d %d %d", &n, &m, &k);
for(int i=1;i<=n;i++){
sum[i][0]=0;
for(int j=1;j<=m;j++){
scanf("%d", &a[i][j]);
sum[i][j]=sum[i][j-1]+a[i][j];
}
}
for(int j=1;j<=m-k+1;j++)
dp[1][j]=sum[1][j+k-1]-sum[1][j-1];
for(int i=2;i<=n;i++){
build(1,1,m-k+2,i);
for(int j=1;j<=m-k+1;j++){
modify(1,j,j+k,-a[i][j+k-1]);
dp[i][j]=sgt[1].mx+sum[i][j+k-1]-sum[i][j-1];
modify(1,max(j-k+1,1),j+1,a[i][j]);
}
}
int ans=dp[n][1];
for(int j=2;j<=m;j++)
ans=max(ans,dp[n][j]);
printf("%d\n", ans);
}
int main(){
int T=1;
// scanf("%d", &T);
while(T--){
solve();
}
return 0;
}
