Polya原理-模型整理

我个人认为它的难度等级为省选，比杜教筛略简单（因为公式肥肠好背，证明认真看的话是可以看懂的）
推荐一篇好的学习资料https://zhuanlan.zhihu.com/p/350711725
Burnside公式：

Polya公式：

温馨提示：有时候染色时有限制条件，不能用Polya公式，需要用dp或是其他算法求在每个置换下不改变的方案数，然后上Burnside
现在我整理了几个Polya原理的模型：
1）方格染色问题
给定n*n大小的方格，有m种颜色，问有多少种不同的染色方案（经过旋转得到同一种方案的算一种方案）
有4种置换，置换集合={转0°，转90°，转180°，转270°}
分类讨论：
----1.n为偶数
--------转0°时循环节个数是方格的总面积
--------转90°和270°时循环节个数是方格的总面积/4
--------转180°时循环节个数是方格的总面积/2
----2.n为奇数
--------转0°时循环节个数是方格的总面积
--------转90°和270°时循环节个数是(方格的总面积-1)/4+1
--------转180°时循环节个数是(方格的总面积-1)/2+1(这么做是因为方格的中心是特殊的）
柿子：


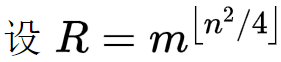
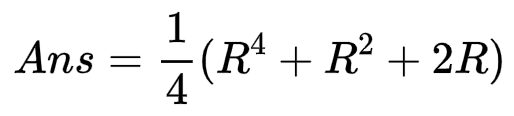
当n为奇数时，还要乘一个m

2）串珠子
给定m种颜色的珠子，每种颜色珠子足够多，要用n个珠子串一个环形手链，如果两个手链经旋转后能够完全重合在一起，对应位置的珠子颜色完全相同，则视为同一种手链。
有n种置换，置换集合={转1个，2个，3个......n个}
在转k个的置换下，循环节的样子和转gcd(k,n)个的循环节样子一样，如果k|n，就显然有n/k个循环节
柿子：

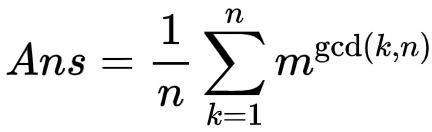
利用反演的思路化一下：

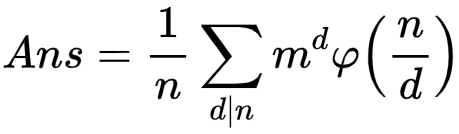
例题：洛谷P4980

3)串珠子升级版
给定m种颜色的珠子，每种颜色珠子足够多，要用n个珠子串一个环形手链，如果两个手链经旋转或翻转后能够完全重合在一起，对应位置的珠子颜色完全相同，则视为同一种手链。
相对于上题，多了翻转操作
先算出旋转同构的贡献：

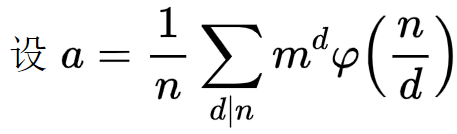
分类讨论：
----1.n为偶数
--------有n*2个置换，其中n个是旋转，n个是一一个对称轴进行翻转
--------有两种对称轴。穿过两个点的对称轴有n/2个，共形成n/2+1个循环节；不穿过点的对称轴有n/2个,共形成n/2个循环节
--------
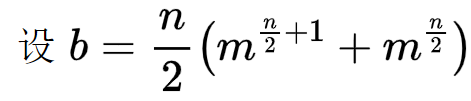
--------可以快速求出翻转同构的贡献
----2.n为奇数
--------有一种对称轴，每条对称轴形成(n-1)/2个长度为2的循环节，1个长度为1的循环节（对称轴一定过一个顶点），共(n-1)/2+1=(n+1)/2个循环节。
--------
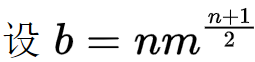
--------可以快速求出翻转同构的贡献
于是，最后的柿子：

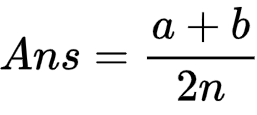
4）正方体边染色
12条边，m种颜色
正方体有24种置换，有：
----1.不动，产生12个长度为1的循环节（1种）

----2.绕着两个对面的中心连线旋转90°/180°/270°，旋转90°/270°时产生3个长度为4的循环节，旋转180°时产生6个长度为2的循环节（有3组对面，3*3=9种）

----3.绕着两个对边的中心连线旋转180°，产生5个长度为2的循环节和2个长度为1的循环节（有6组对边，6种）

----4.绕着两个对点的中心连线旋转120°/240°，产生4个长度为3的循环节（有4组对面，4*2=8种）
1+9+6+8=24
柿子不放了，太恶心

5）完全图的置换
给一个完全图的边染色，两个图是同构的，当且仅当可以改变一个图的顶点编号，使两个染色图完全相同，有n个顶点，m种颜色，求本质不同的染色图个数
1<=n<=53
n这么小，一定含有一部分的暴力成分
显然有n！种关于点的置换，不能暴力枚举全排列再挨个计算循环节长度。可以枚举循环节大小，再乘上这样的循环节的出现次数
具体地，枚举循环节大小其实就是枚举若干正整数，使得加和等于n（不可以通过修改一些数的位置使这次枚举的内容和之前枚举内容一样），这个操作的时间复杂度是个玄学，总之枚举数量不会太多，用dfs玩玩就行。
就算确定了每个点循环节的大小，还要确定一个点循环内的边循环个数和点循环之间的边循环个数
分类讨论：
--1.一个点循环节内的边循环数量，设点循环节长度为i
----1.1这个点循环节长度是奇数
------
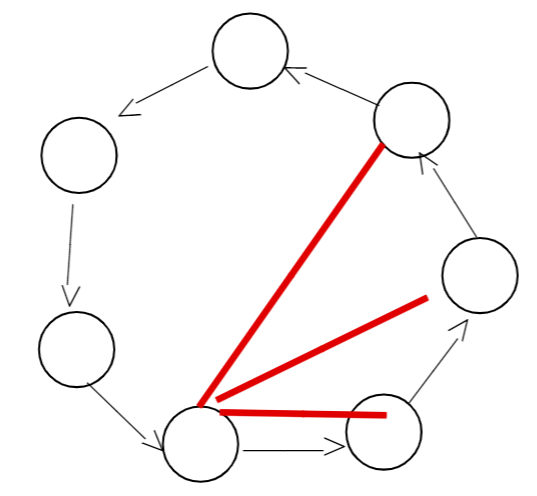
------如图，黑色箭头代表点循环内的这个点的置换后的位置，红色边代表可以以这条边为开始作为一个边循环节，且每个红色边所代表的循环节互不相等
------这种边共有(i-1)/2个，所以这一部分的边循环数为（i-1)/2
----1.2这个点循环节长度是偶数
------根据1.1的思路，易知这一部分的边循环数为i/2
--2.连接两个点循环节的边循环数量，设其中一个点循环节长度为i，另一个为j（需要暴力地两两点循环枚举）
----边循环节个数为gcd(i,j)，这里不给出证明，请大家感性理解
在这种点循环下，全部边循环数量记为c
设一种点循环的划分的循环节数量为m，长度分别为l_1,l_2...l_m，我们还要求出将1~n分别放入这m个循环节中，满足第i个循环节中恰好有l_i个点的方案数
可以转换一下，把m个循环转换成m种颜色的小球，i种颜色有l_i个球，n个点转换成n个不同的位置，记S为方案总数，显然有：

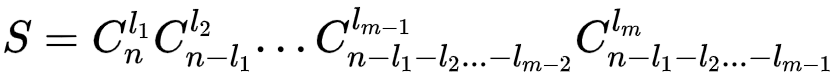
展开，化解，显然等于：

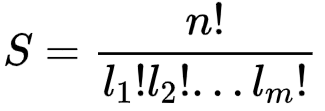
但是，有时l_i会等于l_j(i不等于j且1<=i,j<=m)，这意味着如果将n个位置中i颜色球的位置和j颜色球的位置全部以某方式交换，会和原来的方案重复。这时记点循环长度一共有t种不同的值，这t种值出现的数量为k_1...k_t,则有：

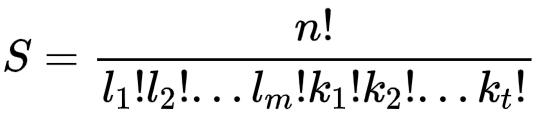
于是，总的答案为：

写完了，好累啊awa
（不要脸地求求您给我点个赞）

6）洛谷上还有一些题，未完待续...