五一清北学堂培训之数据结构（Day 1&Day 2）

Day 1

前置知识：

二进制

2.基本语法

3.时间复杂度

正片

1.枚举

洛谷P1046陶陶摘苹果入门题没什么好说的

判断素数：从2枚举到sqrt(n),若出现n的因子，则n是合数

因为数据范围比较小，所以直接欧拉筛，再判定在l~r区间内的数

代码......被我吃了

好题*1

显然暴力枚举dfs不现实。

所以我们要想点办法（废话）

用ai来表示第i个数是否选中，不选是0，选是1

把每个ai写下来。拿样例的第一个举个例子，就是1110(3选，7选，12选，19不选)

我们发现，写下来后就是一个二进制数，这样组成的每一个二进制数就能代表一种状态，而且不会重复表示。

这样我们枚举状态，就是在枚举000……0（n个0）到111……1（n个1）的所有二进制数

为了方便，我们把它转为十进制数进行枚举，上限就是2^n。

代码（咕咕咕~~~~）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n,m,a[21],ans;
int check(int x)
{if(x<=1)return 0;//注意特判 
 for(int i=2;i<=sqrt(x);i++)
  if(x%i==0)return 0;
 return 1;
}
void make_ans()
{  for(int i=0;i<(1<<n);i++)
   {
        int tmp=0,sum=0;
         for(int j=0;j<n;j++)
         {
             if((1<<j)&i)//2^k的二进制表示只有第k位是1，其余是0，看枚举的二进制数上哪一位是1
             {   
                 tmp++;
                 sum+=a[j];//就选那一位对应的数 
        }
      }
      if(tmp==m)//如果选够m位就判断sum 
      {ans+=check(sum);
      }
   }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
     scanf("%d",&a[i]);
    make_ans();
     printf("%d",ans);
}

练习：求L到R中有多少数既是回文数又是素数

1<=L<=R<=10^7

显然枚举素数，再判回文数的话会炸

那我们不妨换个东西枚举，我们枚举回文数。

对于回文数来说，正着读和倒着读都一样，并且只要知道了一半，另一半也就知道了。所以我们直接枚举回文数的一半，再拼出另一半，看是否是素数。对于偶数位的回文数来说，要枚举k/2位（k为位数），奇数位回文数要枚举k/2+1位，而是偶数位数的回文数一定是11的倍数，不用管。

代码如下（本人口胡的....应该是对的吧，要是不对欢迎纠错）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n,m,a[21],ans;
int l,r;
int make_size(int x)//统计位数 
{int an=0;
  while(x)
  {an++;
   x/=10;
  }
  return an;
}
int ksm(int x,int b)//快速幂的板子（待会分治要讲） 
{int r=1;
  while(b)
  {if(b&1)r*=x;
   x*=x;
   b/=2;
  }
  return r;
}
int huiwen(int x)//制作回文数 
{int a[10],y,z=0;
memset(a,-1,sizeof(a));
int m=x;
  while(m)
  {y=m%10;
   m/=10;
   a[++z]=y;
  }//把原数的每一位分出来 
  for(int i=2;i<=9;i++)
  {if(a[i]>=0)
   {x*=10;//进行复制 
     x+=a[i];
   }
  }
  return x;
}
bool check(int x)//判素数 
{if(x<=1)return 0;
  for(int i=2;i<=sqrt(x);i++)
    if(x%i==0)return 0;
 return 1;
}
int main()
{ scanf("%d%d",&l,&r);
  int size_l； 
  size_l=make_size(l)/2;//因为是枚举回文数的一半再复制，所以从l位数的一半开始枚举（这里计算l的位数） 
  int kk=ksm(10,size_l);//初始的回文数的一半 
  for(int i=kk;huiwen(i)<=r;i++)//制作的回文数不大于r才能继续循环 
  {int m=huiwen(i);//制作回文数 
   if(check(m))ans++;//check判素数（也可以预处理）（我懒） 
  }
  printf("%d",ans);
}

枚举的优缺点

所以我们枚举时最好利用一些性质进行枚举

2.搜索

搜索本质上是一种枚举，但是可以表达一些枚举不方便表述的状态

（接下来的东西会越来越难，so有些太难的就不写代码了）

搜索分为深搜和广搜

深搜

也就是dfs(大法师)

举个例子

有多组数据

看的出来，深搜复杂度玄学，所以深搜剪枝是很重要的。

虽然不是澡堂讲的，但我觉得写一下还是有必要的。

大法师dfs剪枝小技巧：

1.在某一顺序会造成很多不明错误时，不妨换一下搜索顺序。

2.如果有几种情况是等效的，那只需对其中一种情况进行搜索

3.及时对当前状态进行检查，如果到了边界，就立即回溯，不要继续搜下去（能省不少时间），也叫上下界剪枝

4.在最优化问题搜索中，如果当前花费超过已找到的最优解，就立即返回。因为继续搜下去，花费一点比最优解大。

5.记忆化搜索

不难看出，在上面的代码中，数据一多就会TLE。这是因为进行重复计算浪费了大量时间。解决办法就是在第一次计算时，将算出的每个f(n)记录下来，搜索到这一项时直接返回，不再进行递归。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
long long n,f[1000001],t;
long long ff(int n)
{ if(n==1)f[n]=1;
  if(n==2)f[n]=1;
  if(f[n])return f[n];
  else 
  {f[n]=ff(n-1)+ff(n-2);
   return f[n];
  }
}
int main()
{  
    scanf("%lld",&t);
    for(long long i=1;i<=t;i++)
    {scanf("%lld",&n);
     printf("%lld",ff(n));
    }
}

输出一种方案

如果有多组解，按字典序输出

这道题看起来让人质壁分离。

我们要用dfs,因为用dfs空间会炸掉。

因为要字典序，所以我们遵循先h再o的顺序搜就好了（代码什么的真好吃）

虽然fz说鬼畜的题用广搜，but这里我们用深搜，

why?广搜你怎么存状态？？？

我们在正方形里，从低到高，从做往右枚举要填进来的正方形（就是维护正方形的下轮廓）

随便举个例子

图中的数字表示枚举的点的顺序

有一个小优化：不重复选用边长相同的小正方形

广搜

广搜主要注意状态的确定。

广搜主要应用之一：迷宫（以下题目100%只说思路，没有代码233）

前面说过，广搜的要点是状态的确定。这里的状态是每个格子的填法。我们可以将每一种填法对应一个数，再用vis[i]记录是否出现过当前状态。

如果有多个数据，就从结果开始搜，搜到初始状态。

代码太难惹2333以后再说qwq。

这里可以经过障碍物。在正常的情况下，障碍物是不能经过的。但这里不正常，所以我们记录状态也不能用正常的记录方式（记录当前步数），而是要记录当前经过的障碍物数。显然，当前经过的障碍物数越小越好，所以我们先扩展当前经过障碍物数量最小的点。而一直遵循这个原则，我们记录的点就只会出现k和k+1这两种状态（k为当前经过障碍物数）。所以我们只要维护两个队列（k和k+1就行了），每次扩展点的时候，扩展同一层的点。

别看题目描述的乱七八糟，其实它就是个暴力。

用四维数组记录人和箱子的位置（人的位置对箱子的方向有影响）然后暴力就是了。

记住，鬼畜的题一般都用广搜，例如下一道

数据保证只有三个固体块（不多也不少）

够鬼畜吧。（当年华容道这游戏虐的我不成人样233）

因为这里固体块不会旋转。所以我们可以用每个固体块的任意一小块来代替这个固体块。在这里我们用每个固体块左上角的小块来代替。

同时以一开始覆盖所以固体块的大矩形为“底”，建立坐标系。

例如：

这样就可以方便的表示每个固体块了。

但因为每种状态是由三个固体块的位置构成，所以要用6维数组，记录每个固体块左上角的坐标。

维度太大，试着降维。

那就固定一个固体块的左上角，使其永远是（0,0），如果该固体块要移动，那就让它旁边的固体块做相对运动。

这样固定下来的固体块的位置就不用讨论了。6维-->4维

再进行广搜，对每个固体块该怎么移动就怎么移动，以及判断一撮balabalabala...........................

这里我们就不管期望了。

多源多汇最短路详情请见明天。
bfs另一个用途：

图论

存储：1.邻接矩阵（空间：n^2）(便于加删)

2邻接表(vector)(访问较快，删除麻烦)（较慢）

vector：存储

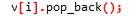弹掉最后一个

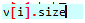计算长度

（还是前向星适合我）

贪心：

每一步选取当前最优。

当不确定时,把多个贪心策略拼一起可以骗分

按照牛奶单价排序，选取即可

让体积最大的和最小的放一个箱子里，如果没有能配成对的就单着

把式子化简一下：

Ai*j-Ai+Bi*n-Bi*j=j*(Ai-Bi)+(n*Bi-Ai)

红字为常数，不用管，然后对(Ai-Bi)排序

这里式子中的Ai不是最大出水量，是0到最大出水量之间的一个数

依旧是化简一下式子：

Σ(Ai)*T=Σ(Ai*ti)=Σ(Ai*T)

ΣAi（ti-T）=0

这里肯定会有

1.ti-T>0 2.ti-T<0

如果得到的水最终的温度是T，就得让这两边的水互相“中和”。又要让最终的总水量尽可能大，所以少的那一边必定全部选上，多的那一边剩余的就不选了

//代码 from fz
#include<cstdio>
#include<algorithm>
#include<cstring>

#define N 300005

using namespace std;

int a[N],t[N],i,j,m,n,p,k,id[N],ID[N],sum[N],T;

double ans;

int cmp(int x,int y)
{
        return sum[x]<sum[y];
}

int main()
{
        scanf("%d%d",&n,&T);
        for (i=1;i<=n;++i) 
        {
                scanf("%d",&a[i]);
        }
        for (i=1;i<=n;++i) scanf("%d",&t[i]);
        for (i=1;i<=n;++i)
        {
                if (t[i]==T) ans+=a[i];
                else if (t[i]<T) id[++id[0]]=i,sum[i]=T-t[i];
                else ID[++ID[0]]=i,sum[i]=t[i]-T;
        }
        sort(id+1,id+id[0]+1,cmp);
        sort(ID+1,ID+ID[0]+1,cmp);
        long long suma=0,sumb=0;
        for (i=1;i<=id[0];++i)
            suma+=1ll*sum[id[i]]*a[id[i]];
        for (i=1;i<=ID[0];++i)
            sumb+=1ll*sum[ID[i]]*a[ID[i]];
        if (suma<sumb)
        {
                swap(suma,sumb);
                for (i=0;i<=n;++i) swap(ID[i],id[i]);
        }
        for (i=1;i<=ID[0];++i) ans+=a[ID[i]];
        for (i=1;i<=id[0];++i)
            if (1ll*sum[id[i]]*a[id[i]]>=sumb)
            {
                    ans+=1.*sumb/sum[id[i]];
                    break;
            }
            else
            {
                    ans+=a[id[i]];
                    sumb-=1ll*sum[id[i]]*a[id[i]];
            }
        printf("%.10lf\n",ans);
}

作业问题：

有n项作业，第i项作业需要ai天完成，而某人希望在第bi天完成这项作业。设ci为第i项作业写完的那一天，则ci-bi就是第i项作业的延迟调度，求最小的延迟调度之和。

我们用策略3.

反例？忘了(@wwww@)

二分

洛谷P2678跳石头

最大距离最小：

设最大距离为mid，看是否可行。

判是否可行：尽量远

mid>=k时，合法，mid<=t时，不合法（k,t为某个数）

二分k,t(最开始t=最大上界(1e9))

这道题看起来是贪心，然而它是二分

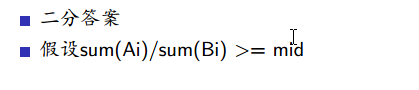
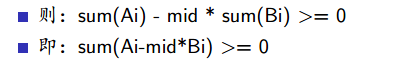
总结：用二分把问题变为判定性问题

三分

三分用来计算这种东西的峰值

分治

复杂度：只和k的二进制数位有关

归并排序

|---------------------------------------------------------------------------|

->|-------------------------------------| |----------------------------------|

->|------------------||----------------| |---------------||-----------------|

就类似这样（这是分）

for example:

3 8 6 7

选出3，第一个的左指针右移

-->选出6，第二个的左指针右移

-->如此循环

For example:

/ | \

7 1 7

/ | \ / | \

3 1 3 3 1 3

/ | \ / | \ / | \ / | \

1 1 1 1 1 1 1 1 1 1 1 1

对于每个编号i来说，分治查看i在那棵子树里。

举个例子：i=10;

将上面这棵树从中间分开，中间编号i=8,显然10>8,所以编号为10的元素在右边这棵子树中，再查看下面(图1)这颗树（原图中右边的子树），i此时变为10-8=2，发现i在左边的这棵树(图二)中的第二个元素，是1.

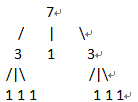
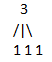
图1 图2

旷世好题之平面最近点对

欧几里得距离就是sqrt((x1-x2)^2+(y1-y2)^2)(就是两点间距离公式)

Day 2

二叉搜索树：

这个比较简单，只需要在每次加入时比较加入的数和当前最大的数，然后更新就行了。

这里扯到了删除，所以就没有上一个题那么简单了。

这时候我们用到了二叉搜索树。

什么是二叉搜索树？

for example

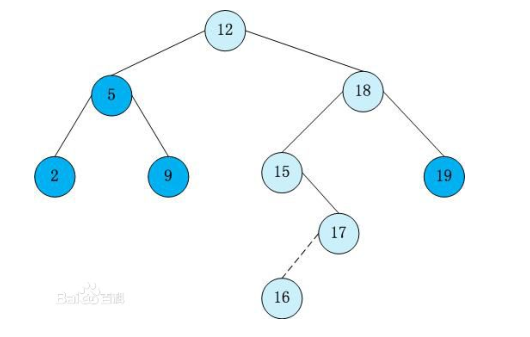
这就是一棵二叉搜索树。

二叉搜索树性质：

对于每一个结点来说，它的左子树严格小于它，右子树严格大于它（这里不讨论有相同数的情况）

我们要利用二叉搜索树来完成这个操作。

因为每个结点左边的值都比右边小，所以要求最小值，就找左儿子，如果没有左儿子的话，那这个点就是最小值。

int findmin()
{
  intx=root;
  while(ls[x])x=ls[x];//只要有左儿子，就继续走
  return key[x];//返回最小值（权值）
}

插入：

我们既要插入，又要维护整棵树的形态，所以我们从根节点开始插入，与当前结点比较。我们用key[root]表示当前点的权值，root为当前点，x为要加入的点的权值。我们比较key[root]和x.

如果key[root]<x,x那就说明x在root的右边，与root的右儿子比较，如果key[root]>x,就将x与root的左儿子比较，最终完成插入

下面的root表示根节点

void put(int x)
{   sum[++tot]=x;//用tot表示二叉树结点的个数
    size[tot]=1;
    if(!root) root=tot//如果没有结点，就让它有结点
    else
    {
         int now=root;//从根开始
         while(true)
         {++size[now];//size[i]表示点i的度（也就是i下面的点数+1）
          if(sum[now]>sum[tot])//判断要插入的点和当前点
           {
             if(!ls[now])//如果当前点没有左儿子
             {
                 ls[now]=tot;fa[tot]=now;//插入，插完就跑
                 break;
             }
             else now=ls[now]//如果有左儿子，就继续比较（按左儿子找）
           }
           else
              {if(!rs[now])
                {rs[now]=tot;fa[tot]=now;
                    break;
                }
               else  now=rs[now];
              }
         }
    }
}

fz鬼才缩进！

删除：

step1.定位结点

从当前点开始，就像刚才插入一样寻找。

int find(int x)
{
     int now=root;
     while(key[now]!=x)
        if(key[now]<x)x=rs[now];//如果当前点的权值比x小，说明x在右子树里
        else  x=ls[now];//否则就在左子树里
     return now;
}

step 2.删除：

我们这里不选择把点置零。（会造成各种奇奇怪怪的困难）

我们考虑点x的儿子的情况。

如果没有儿子，就直接删了

如果有一个儿子，直接让它的儿子认它的父亲为父，然后删掉。

如果有两个儿子，就找到这个点右子树中权值最小的结点y，作为x的后继。然后把y和x的父亲暴力一拼，删除x.就像下图

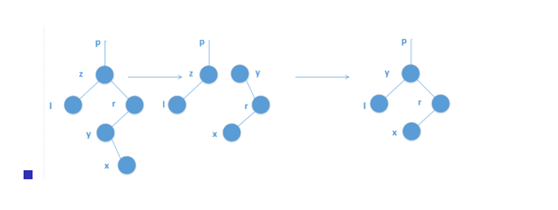
int find(int x)//查询值为x的数的节点编号 
{
    int now=root;
    while (sum[now]!=x&&now)
    if (sum[now]<x) now=rs[now]; else now=ls[now];
    return now; 
}
void del(int x)//删除权值为x的点
{
     int  k=find(x),t=fa[k];//找到x的父节点
     if(!ls[k]&&!rs[k])//如果x既没有左儿子，又没有右儿子
      {
          if(ls[t]==k)ls[t]=0; else rs[t]=0;//x的父亲就没有儿子了
         for(int i=k;i;i=fa[i])   size[i]--;//从x点开始，把它的每个祖宗的度-1       
      }
    else if
      (!ls[k]||!rs[k])//只有一个儿子
      {
               int child=ls[k]+rs[k]//把x的儿子的编号弄出来
               if(ls[k])ls[t]=child; else  rs[t]=child;
      }
    else
       {int y=rs[k];while(ls[y])y=ls[y];//找后继
          if(rs[k]==y)//如果后继是x的右儿子
         {if(ls[t]==k)ls[t]=y;else rs[t]=y;
           fa[y]=t;
           ls[y]=ls[k];
           fa[ls[k]]=y;
           for(int i=k;i;i=fa[i])size[i]--;
           size[y]=size[ls[y]]+size[rs[y]];
          }
         else//最可怕的情况
           {  for(int i=fa[y];i;i=fa[i]) size[i]--;
               int tt=fa[y];
               if(ls[tt]==y)
               {ls[tt]=rs[y];//如果y是它爹的左儿子，那就让y唯一的儿子（右儿子）代替y原本的位置（y要提上去）
                 fa[rs[y]]=tt;
                }
              else
              {rs[tt]=rs[y];
                fa[rs[y]]=tt;
               }
             if(ls[t]==x)//再提x
              {ls[t]=y;//如果x是它爹的左儿子，就更新为左儿子为y
               fa[y]=t;
               ls[y]=ls[k];
               rs[y]=rs[k];
              }
             else
             {rs[t]=y;//按右儿子更新
              fa[r]=t;
              ls[y]=ls[k];
              rs[y]=rs[k];
             }
             size[y]=size[ls[y]]+size[rs[y]]+1;
           }
       }
}

小扩展：

求许多数中第k大的数。

看起来一个sort可以解决的样子

来我们讨论下用二叉搜索树怎么解决

前面我们提到了size[i]，我们用它表示i这个节点子树里节点的个数。

我们从根开始走，如果右子树的size>=k,说明第k大值在右子树里。反之就在左子树里。当然，如果右子树的size+1=k,就说明当前这个点就是最大值。因为右子树的size+1就是当前点的size。这样就可以递归求解了。在每次递归到下一层时，如果到了左子树，要注意把当前的k减去右子树的size,然后-1。

int find_kth(int now,int k)
{
       if(size[rs[now]]>=k)return find_kth(rs[now],k);//分别对应上面三种情况
       if(size[rs[now]]+1==k)return  key[now];
       return find_kth(ls[now],k-size[now]-1);
}

对于正常插入和删除的size维护可以总结为一下几点：

插入：沿路增加。

删除：1.size[fa[i]-1](无儿子)

2.只有右儿子：沿路的父亲节点size-1

3.左右儿子都有：从y往上一直到x的父亲，一路-1.（具体代码中都有）

二叉搜索树排序：

这里我们要用到二叉搜索树的性质。

对于二叉搜索树来说，每个结点的左子树严格小于它，即左子树中不会有权值比它大的点，而右子树严格大于它，即不会有权值比它小的点。这样我们做一次中序遍历就可以得到一个排序了。

中序遍历：遵循左中右原则。

举个例子：

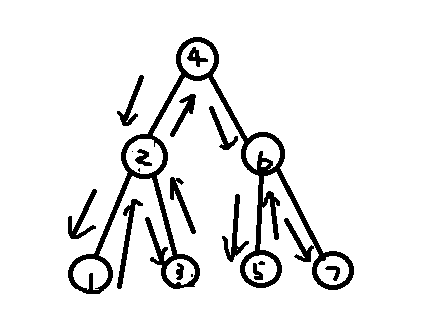
箭头为遍历顺序，点上的数字为输出的顺序

深搜即可解决

int dfs(int now)
{
   if(ls[now])dfs(ls[now])
   printf("%d",key[now]);
   if(rs[now]) dfs(rs[now]);
}

就像第二个例子，画出来的树是成链的

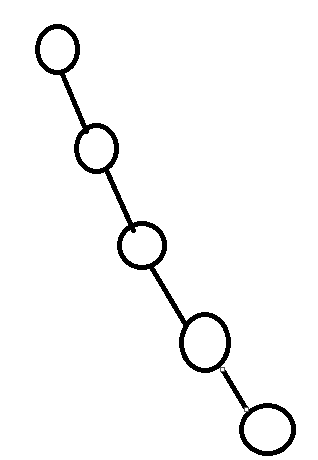
这种数据遍历起来复杂度就有点崩溃（复杂度为树的高度）

二叉堆

基础

我们可以手写，也可以用系统堆（个人感觉还是优先队列好用qwq）

这里注意一下堆的插入是从下一路向上比，而二叉搜索树是从根节点一路往下比。

修改一个点的权值：

咦，为什么没有删除最小值?

删除最小值只要把一个权值改到无穷大就能解决辣

比较简单的是把一个权值变小。

那只要把这个点像插入一样向上动就行了。

权值变小：上浮（就是从下往上比）

权值变大：下沉（就是从上往下比）

定位问题：

寻找权值为x的点的编号；

假设权值两两不同，再记录一下某个权值现在哪个位置。（用辅助数组pos[权值]=位置）

在交换权值的时候顺便交换位置信息。

int find(int x)
{
    return pos[x];
}
void up(int now)
{
    while(now&&a[now]<a[now/2])
     {swap(a[now],a[now/2];
      swap(pos[now],pos[now/2]); //注意pos要跟着一起变
       now/=2;
     }
}
void down(int now)
{
    while(now*2<=n)
    {if(a[now]>a[now*2])
          {swap(a[now],a[now*2];
            swap(pos[now],pos[now*2]);
            now*=2;        
           }
     else
        {
              if (a[now]<=a[now*2]&&a[now]<=a[now*2+1]) break;
          if (a[now*2]<a[now*2+1]) 
               { swap(a[now],a[now*2]);
                  swap(pos[now],pos[now*2]);
                   now*=2;
                }
          else 
              {swap(a[now],a[now*2+1]);
                swap(pos[now],pos[now*2+1]);
                now=now*2+1; 
         }
     }
}
//以上是变换

删除：先赋值为inf,再下沉（元素会特别多）

可以把最后一个结点放到根上，然后再下沉（与此同时n - -）

应用：

堆排序

把数全部插进去，每次询问最小值，然后把根删掉就行了.

看道题：

丑数

丑数指的是质因子中仅包含2,3,5,7的数，最小的丑数是1,求前k个丑数。

K ≤ 6000

看起来好像可以打表，但这样不优雅。

ps:打表小技巧：把要打的数拼尽全力转为100进制用字符串存，省时间省空间费脑子。

（也可以打一个巨长的表卡编译器10min）

好了说正经的。

我们选中x后，接下来我们要选2x,3x,5x,7x,我们把这些数塞进堆里，每次取的时候和上一次取出来的数比较，如果不同，就输出，并且计数器+1，如果相同，就不要。因为堆是有序的，而且我们维护的是一个小根堆。

一些方便的东西：

1.queue

queue里面有一个叫priority_queue,也就是所说的优先队列。这是一个大根堆，不过我们可以做点什么让它变成小根堆。

例如这样

函数：

q.push() 插入

q.top() 返回

q.pop() 弹掉

q.clear() 清空

2.set（高级的二叉搜索树）

st.insert( x )插入（不会插入两个相同的东西）

st.erase( x )删除

st.find( x )看是否存在某个数

st.lower/upper bound():

lower_bound( x ):找到第一个大于等于x的数的地址。

upper_bound( x ):找到第一大于x的数的地址

st.begin()/st.end()取最小/最大值后面的一部分

ser<int>::iterator it=st.lower_bound(x)

上面的it可以进行：it++ or i--(其他操作不行)

set可维护有序数组（可以代替系统堆（可能有点慢233，不过操作多））

区间RMQ问题：

给出一个长度为N的序列，我们会在区间上干的什么(比如单点加（给一个点加），区间加（给一个区间内的所有点加），区间覆盖),并且询问一些区间有关的信息(区间的和,区间的最大值)等。

例一：

给出一个序列，每次询问区间最大值.

N ≤ 100000,Q ≤ 1000000.

我们先抛开最大值不谈，如果这个题要求和的话，只用求出前缀和就好，因为[l,r]的权值之和等于[1,r]-[1,l-1].

那我们回到这个题，是否可以模拟求和的思路，通过求出类似前缀和的东西，来求出区间的的最大值呢？当然可以。这道题所有的数给定后就不会动了，所以这是个静态的。并且是可重复计算（可重复计算特指求最大值或最小值），我们就可以用st表。

st表思想：

先求出每个[i,i+2^k)的最值，然后找出两个区间包住询问的区间，这两个区间的最值就是答案。

我们注意到这样的区间总数是nlogn的（i有n个，k有logn个）

这个题里，我们不妨设f[i][j]是[i,i+2^j)的最小值。

首先，f[i][0]都是i.

其次，f[i][j]=min(f[i][j-1],f[i+j-1][j]);下面这个图就可以解释一下

|------------| |------------|

i i+2^(j-1) i+2^j

知道了这些，就可以处理整个st表了。

那如何寻找那两个区间？

先找最大的k满足2^k<=r-l+1（r-l+1是整个区间的长度）

我们找到这样的k,那[l,l+2^k),[r-2^k+1,r+1）这两个区间自然就能包住整个[l,r),而且不会出现[l,r]之外的部分。

|--------------------| 区间[l,r]

|---------------| 区间[l,l+2^k)

|----------------|区间[r-2^k+1,r+1）

这是图示

找到这两个区间后，f[l][k],f[l+2^k+1][r]中较小的一个就是答案。这样每次询问时只需要找区间，复杂度o(1)

再来看一道

给出一个序列，支持对某个点的权值修改，或者询问某个区间的最大值.

N,Q ≤ 100000.

这道题和刚才那道题的区别就在于这里每个点的权值是有可能变的，所以就不再是静态的，而是动态的。那我们还能不能继续用st表做呢？试一下。

比如改5这个点.

j = 0 改了一个位置，嗯，完美.

j = 1 改了两个位置4,5,稳.

j = 2 改了四个位置2,3,4,5,还行

j = 3,emmmmmm好像不太妙。

我们注意到当j往上走的时候，要改的区间个数是这个点的编号。j是指2^j的那个j.

看来现在修改一侧就要修改O（N）个点

看起来会炸

既然st表不靠谱，那咋办？

那我们肯定就不能用静态求最值的东西了。我们换一个动态的。

线段树

本质是一棵不会改变形态的二叉树.

树上的每个节点对应于一个区间[a,b](也称线段),a,b通常为整数

同一层的节点所代表的区间，相互不会重叠

同一层节点所代表的区间，加起来是个连续的区间

对于每一个非叶结点所表示的结点[a,b]，其左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b](除法去尾取整）

就像下面：

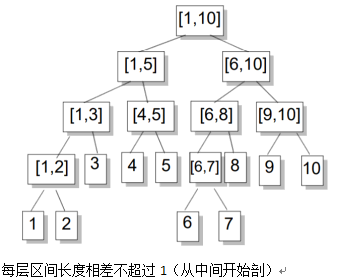
这里的从中间开始是指该结点的两个儿子是由它从中间剖开得到的。

这个线段树也演示了一个区间拆分的过程。

区间拆分：

将一个区间[a,b]拆成若干个结点，使这些结点加起来还是区间[a,b]，且互不重叠。对于在[a,b]内的一个区间[l,r]来说，如果在区间拆分过程中拆出的结点所代表的区间在[l,r]内，就称这个结点为终止结点。这个拆出来的区间就是终止区间。

和st表有什么区别？

1.st表是静态的，而线段树是可以动态的。

2.st表会有重叠，而线段树不会有重叠。

如何进行区间拆分？

从根节点[1,n]开始，考虑当前节点是[L,R].

如果[L,R]在[a,b]之内,那么它就是一个终止节点.

否则,分别考虑[L,Mid],[Mid + 1,R]与[a,b]是否有交,递归两边继续找终止节点.

哪边有交就往哪走

来我们看几道好题。

一.给一个数的序列A1 ,A2 ,...,An .并且可能多次进行下列两个操作：

1.对序列里面的某个数进行加减

2.询问这个序列里面任意一个连续的子序列A i ,A i+1 ...A j 的和是多少.

希望单个操作能在O(logN)的时间内完成.

通过阅读上下文可知这题要用线段树。

运用线段树，每个区间要记录的是？

ΣAi

对于操作1，我们相当于对[i,i]做了一个区间拆分（最后要拆出来[i,i]）,沿路我们找到所有的祖先结点，维护记录的和（每个结点的答案为它的左儿子+它的右儿子）。

对于操作2，我们对给的区间[l,r]做一个区间拆分，将拆分出的每一个终止结点的和累加起来就是答案。（代码什么的先不管了233）

二

给定Q个数A 1 ,...,A Q ,多次进行以下操作:

1.对区间[L,R]中的每个数都加n.

2.求某个区间[L,R]中的和.

Q ≤ 100000

乍一看，好像见过。

哎这不对啊，咋是区间加呢？说好的单点加呢？

区间加，我们就得好好考虑考虑了。暴加一定会炸。

大家都遇到过拖更的现象吧。在这里我们也采用拖更这种想法。先把要加的数用inc记下来，要是询问到这个区间，就加上，不然就不加了，还省时间。在区间增加时，如果要加的区间正好覆盖一个结点（也就是到了终止结点），就增加其inc和sum（这里sum是当前结点的真实值），不再往下走。

回来更新：由左右儿子加和。

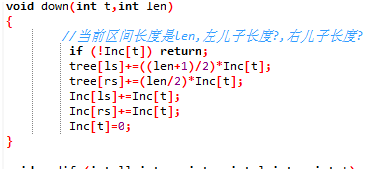
拖更思想更新延迟的代码

旷世好题*2

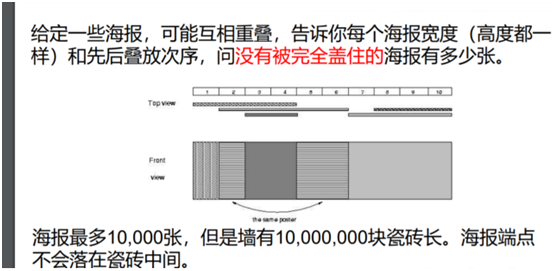
显然这里砖多的令人头疼。咱想想办法给他降一下数量。既然要降砖块的数量，那就不能管砖的面积是多大了。

我们把所有海报端点去重排序最终可以降成4w块

因为海报的端点最多20000个（这里的“端点”是海报的边的横坐标），一定有海报中间的部分跨过好几块砖，我们就把那好几块砖视作一块

那么我们从最底层的海报开始，一张一张往上贴.

对于一个区间[L,R],我们记录的信息是这个区间整体被第几张海报覆盖了,初始值设为−1. (区间拆分and延迟更新)

对于一张包含[L,R]的海报i,我们就只需要把[L,R]里面所有的位置都赋成i就可以了。

注意利用区间分解和延迟更新的方法.

本题中是否会有标记时间冲突的问题?(先来的覆盖后来的)

不会发生，只有可能后来的覆盖先来的。

这样我们结合延迟更新的思想，将每一块的标记向下传。

给出长度为N的序列A,

Q次操作，两种类型:

(1 x v),将A x 改成v.

(2 l r) 询问区间[l,r]中有多少段不同数。例

如2 2 2 3 1 1 4,就是4段。

N,Q ≤ 100000.

这里我们用线段树只记录每个区间的段数一定会出错。为什么呢？线段树区间拆分过后，会把整个大区间分成n个小区间，每个区间的段数都由它的左右儿子的段数相加得来。but真的对吗？

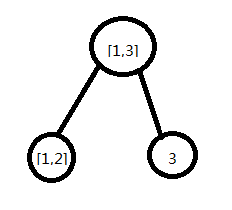
我们摘出来线段树的一部分，这里[1,2]和3的段数都是1，但[1,3]的段数还是1。原因就在于我们合并区间时，会出现[1,2]最右边和3最左边的数相同的情况。为了保证正确性，我们不仅要记录每个区间的段数，还要记录每个区间最左边和最右边的数。

若合并时遇见相同，就段数加起来-1，否则就加起来

树状数组

树状数组：常用来求前缀和。

什么是树状数组？

先看一下这棵树

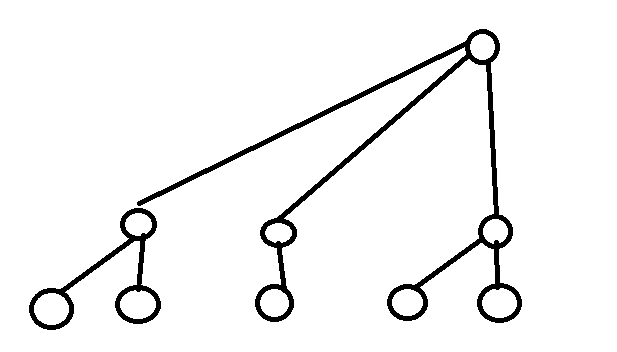
这样偏了一下，就是树状数组的结构。

对于树状数组C,C[i]=A[i-lowbit[i]]+...........+A[i].

什么是lowbit?简单来说就是i&(-1)

为什么？我也不知道呀

前缀和是指A1+A2+A3+A4+A5+...............+Ak，可以拆成C[k]+C[m]+C[t]+...........

其中m=k-lowbit(k),t=m-lowbit(m)......为什么呢？自己举几个例子就知道了。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<set>
#include<vector>
#include<map>
#include<queue>

#define N 300005
#define M 8000005

#define ls (t<<1)
#define rs ((t<<1)|1)
#define mid ((l+r)>>1)

#define mk make_pair
#define pb push_back
#define fi first
#define se second

using namespace std;

int i,j,m,n,p,k,C[N],a[N],b[N];

long long ans;

int lowbit(int x)
{
        return x&-x;  
}

void ins(int x,int y)//修改a[x]的值,a[x]+=y;
{
        for (;x<=n;x+=lowbit(x)) C[x]+=y; //首先需要修改的区间是以x为右端点的,然后下一个区间是x+lowbit(x),以此类推 
}

int ask(int x) //查询[1,x]的值 
{
        int ans=0;
        for (;x;x-=lowbit(x)) ans+=C[x]; //我们询问的]是[x-lowbit(x)+1,x,然后后面一个区间是以x-lowbit(x)为右端点的，依次类推 
        return ans;
}

int main()
{
        scanf("%d",&n);
        for (i=1;i<=n;++i) scanf("%d",&a[i]),b[++b[0]]=a[i];
        sort(b+1,b+b[0]+1); b[0]=unique(b+1,b+b[0]+1)-(b+1);
        for (i=1;i<=n;++i) a[i]=lower_bound(b+1,b+b[0]+1,a[i])-b;
        for (i=1;i<=n;++i) ans+=(i-1)-ask(a[i]),ins(a[i],1);
        printf("%lld\n",ans);
}

有什么用呢？

我们可以用前缀和相减的方式来求区间和.询问的次数和n的二进制里1的个数相同.是O(logN).求一个数组A 1 ,A 2 ,...,A n 的逆序对数.n ≤ 100000,|A i | ≤ 10 9 .

我们将A 1 ,...,A n 按照大小关系变成1...n.这样数字的大小范围在[1,n]中.（就是离散化）

维护一个数组B i ,表示现在有多少个数的大小正好是i.

从左往右扫描每个数,对于A i ,累加B A i +1 ...B n 的和,同时将B A i 加1。

时间复杂度为O(N logN).

LCA

在一棵有根树中,树上两点x,y的LCA指的是x,y向根方向遇到到第一个相同的点。

比如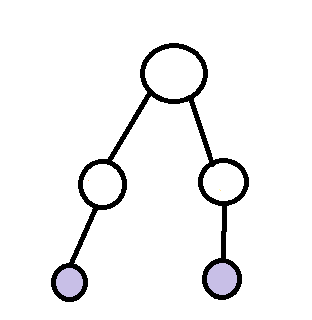：这个图中的两个蓝色的结点的LCA就是根结点。

求法：

我们记每一个点到根的距离为deep x .注意到x,y之间的路径长度就是deep x + deep y − 2 * deep LCA。两个点到根路径一定是前面一段不一样，后面都一样.注意到LCA的深度一定比x,y都要小.利用deep，把比较深的点往父亲跳一格，直到x,y跳到同一个点上. 这样做复杂度是O(len).(每个点跳到公共祖先上)

考虑一些静态的预处理操作.像ST表一样，设fa (i,j) 为i号点的第2^ j 个父亲。

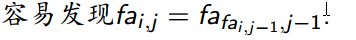
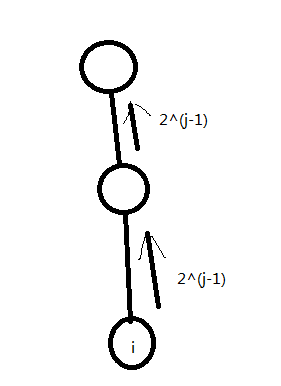就像这个图演示的一样。

思想：st表

利用类似快速幂的想法.（二分）

每次跳2的整次幂，一共跳log次.

首先不放假设deep x > deep y .为了后续处理起来方便，我们先把x跳到和y一样深度的地方.

如果x和y已经相同了,就直接退出.否则,由于x和y到LCA的距离相同,倒着枚举步长,如果x,y的

第2 ^j 个父亲不同，就跳上去.这样，最后两个点都会跳到离LCA距离为1的地方，在跳一步就行了.

时间复杂度O(N logN).

LCA在图论里会发挥很大的作用

倍增

我们之前讲了分治，就是把一个大的东西分成小的，解决每个小的。而倍增就是反过来，从小的翻成大的。

时间复杂度O(nlogn)-O(logn)O(n logn)

并查集

基础

在基础里我们讲到的优化是路径压缩，这里写出所有的优化

优化：

在寻找一个点的顶点时，把这个点的父亲改为其顶点。（路径压缩）（对找爹的优化）
按秩合并。（对合并的优化）

对每个顶点，再多记录一个当前整个结构中最深的点到根的深度deep x .

注意到两个顶点合并时,如果把比较浅的点接到比较深的节点上.

如果两个点深度不同，那么新的深度是原来较深的一个.

只有当两个点深度相同时，新的深度是原来的深度+1.

注意到一个深度为x的顶点下面至少有2 x 个点,所以x至多为logN.

那么在暴力向上走的时候,要访问的节点至多只有log个.

（结合路径压缩复杂度会特别低（不过可能数组会有点问题））

（建议结合暴力找爹）

But路径压缩比按秩合并优秀。不过路径压缩复杂度不严格。按秩合并复杂度严格o(log n)

按秩合并:

void Merge(int x,int y)
{
    x=get(x); y=get(y);// 使用的是最暴力的get
    if (deep[x]<deep[y]) fa[x]=y;
    else if (deep[x]>deep[y]) fa[y]=x;
    else deep[x]++,fa[y]=x;
}