李宏毅2020机器学习——逻辑回归（python 0基础开始）（hw2）

一、作业说明

           1.所给训练集为54256*511的数组，表示54256个人，除了第一列的id索引和最后一列的标签（收入大于等于50000为1，小于50000为0）共有509个特征。

           2.需要完成的任务是根据所给的所有特征来预测这个人收入是否大于50000，典型二元分类问题，采用逻辑回归。

二、作业思路

     首先为数据录入，然后舍去第一列数据，并对数据划分出训练数据和标签数据（为了归一标准化的准确性，这里需要将数据规定为浮点型）。另外，在对提取标签数据时，只提取一列数据，会自动将y设置为一维数组，为了方便后面使用，需要将其重构为m维数组（m为样本数，注意一维数组与多维数组在python中shape的区别，否则会造成内存不够的问题）

import pandas as pd
import numpy as np
import matplotlib.pyplot as pb

data = pd.read_csv('D:/机器学习/数据/hw2/data/X_train')
data = data.iloc[:, 1:]
print(data)
data = np.array(data)
m = np.shape(data)[0]
n = np.shape(data)[1]

X = data[:, 0:-1].astype(float)
y = data[:, -1].astype(float)
y = y.reshape((m, 1))
# X:54256*509
# y:54256*1

# 归一标准化
mean_X = np.mean(X, axis=0)
std_X = np.std(X, axis=0)
for j in range(n-1):
    if std_X[j] != 0:
        X[:, j] = (X[:, j] - mean_X[j])/std_X[j]
pass

     数据初始化，包括权重矩阵，迭代次数，代价函数的值（为了观察其是否在减小），正则系数等，偏置的处理与hw1类似

dim = len(X[0]) + 1
Theta = np.zeros([dim, 1])
ite = 1000
lamb = 1000
learning_rate = 0.01
J = np.zeros([ite, 1])
X = np.concatenate((np.ones([len(X), 1]), X), axis=1)
grad = np.zeros([dim, 1])
mid = np.zeros([dim, 1])
adagrad = 0
eps = 0.0000000001

    sigmoid函数

def sig(x):
    g = np.zeros([len(x), 1])
    g = 1/(1 + np.exp(-x))
    return g

    参数更新，这里使用了传统梯度下降法和Adagrad的算法

for t in range(ite):
    m = len(X)
    hyp = sig(np.dot(X, Theta))
    J[t] = -np.sum(np.log(hyp) * y + np.log(1 - hyp) * (1 - y)) / m + lamb * np.sum((Theta ** 2)[1:]) / (2 * m)
    if t%100 == 0:
        print(str(t) + ":" + str(J[t]))
    mid = -(np.dot(X.transpose(), hyp - y)) / m
    grad = -mid + lamb * Theta / m
    grad[0] = mid[0]
    Theta = Theta - learning_rate*grad
pass

   

for t in range(ite):
    m = len(X)
    hyp = sig(np.dot(X, Theta))
    J[t] = -np.sum(np.log(hyp) * y + np.log(1 - hyp) * (1 - y)) / m + lamb * np.sum((Theta ** 2)) / (2 * m)
    if t % 100 == 0:
        print(str(t) + ":" + str(J[t]))
    mid = -(np.dot(X.transpose(), hyp - y)) / m
    grad = -mid + lamb * Theta / m
    grad[0] = mid[0]
    adagrad += grad ** 2
    Theta = Theta - learning_rate * grad / np.sqrt(adagrad + eps)
pass

      为了清楚看到代价函数的变化，进行绘图，可以看到在迭代次数200次左右，代价函数的变化就比较小了

m = np.arange(0, ite, 1)
pb.plot(m, J)
pb.show()

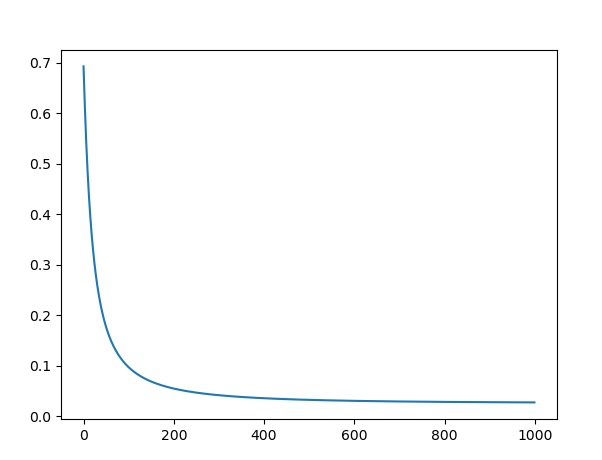
    训练好模型后，需要在测试集上测试模型的好坏，步骤与前面类似

Test_data = pd.read_csv('D:/机器学习/数据/hw2/data/X_test')
Test_data = Test_data.iloc[:, 1:]
Test_data = np.array(Test_data)
X_test = Test_data[:, 0:-1].astype(float)
y_test = Test_data[:, -1].astype(float)
y_test = y_test.reshape((np.shape(X_test)[0], 1))

for j in range(np.shape(X_test)[1]-1):
    if np.std(X_test[j]) != 0:
        X_test[:, j] = (X_test[:, j] - np.mean(X_test[j]))/np.std(X_test[j])
pass

pre = np.zeros(np.shape(y_test))
X_test = np.concatenate((np.ones([len(X_test), 1]), X_test), axis=1)
pre = sig(np.dot(X_test, Theta))
for m in range(len(y_test)):
    if pre[m] >= 0.5:
        pre[m] = 1
    else:
        pre[m] = 0
sum = 0
for n in range(len(y_test)):
    if pre[n] == y_test[n]:
        sum += 1
pass

      下面是两种算法在得到的准确率

梯度下降算法：

 

 

 Adagrad算法：