李宏毅2020机器学习——线性回归（python 0基础开始）（hw1）

一、作业说明

        1、 所给训练集为丰原区2014年整年每个月前20天每天24小时对18种不同检测指标的检测数据，每个月后10天的数据作为测试集来判断模型好坏。

        2、需要完成的任务是根据前九个小时的各个检测指标的数据共同预测第十个小时的PM2.5值。（注意这里应该是从任一小时出发的九个小时）

二、作业思路

        首先是数据的录入数据，由于数据的前三列为文字，采用data.iloc来去除前三列，并将RAINFALL这一行数据的NR取为0（NR表示未降雨）。另外对于从熊猫得到的数据帧可以用to_numpy来得到numpy数组，本作业需要引入pandas、numpy以及matplotlib.pyplot

（缺失可从File→Settings→Python Interpreter→＋搜索后下载）

       注：python与mantlab不同，数组用[]，索引从0开始。

数据录入：

import pandas as pd
import numpy as np
import matplotlib.pyplot as pb

data = pd.read_csv('D:/机器学习/数据/hw1/train(1).csv')

data = data.iloc[:, 3:]
data[data == 'NR'] = 0
raw_data = data.to_numpy()

       数据预处理：先将原始数据按照每个月划分到字典month_data中，利用empty函数创建一个18*480（20*24）的空数组来存储每个月的数据，然后根据需要得到所需的数据集X和标签集y，X的行数为样本数量，列数为特征数。每10个小时的数据作为一组，在这里时间

是连续的，前一天后几个小时加当天前几个小时的数据也是一个样本，则一个月的样本数为471（因为471到480刚好10个小时），特征数为18*9。np.float为强制将数组设置为浮点型，reshape（1，-1）表示将原数组重组为行数为1，列数根据原数组自动确认。

       归一标准化，采用标准差标准化，x' = (x - μ)／σ，然后按照7：5的比例取训练集与测试集。

 

 

 

 

month_data = {}
for month in range(12):
    sample = np.empty([18, 480])
    for day in range(20):
        sample[:, day * 24:(day + 1) * 24] = raw_data[18 * (20 * month + day):18 * (20 * month + day + 1), :]
        month_data[month] = sample
    pass
pass
print(month_data[0].shape)
X = np.empty([12*471, 18*9], np.float)
y = np.empty([471*12, 1], np.float)
for month in range(12):
    for day in range(20):
        for hour in range(24):
            if day == 19 and hour > 14:
                continue
            X[month*471+day*24+hour, :] = month_data[month][:, day*24+hour:day*24+hour+9].reshape(1, -1)
            y[month*471+day*24+hour, 0] = month_data[month][9, day*24+hour+9]
            pass
        pass
    pass
pass

mean_X = np.mean(X, axis=0)
std_X = np.std(X, axis=0)
for i in range(len(X)):
    for j in range(len(X[0])):
        if std_X[j] != 0:
            X[i][j] = (X[i][j]-mean_X[j])/std_X[j]
        pass
    pass
pass

X_test = X[7 * 471:12 * 471, :]
y_test = y[7 * 471:12 * 471]
X = X[0:7 * 471, :]
y = y[0:7 * 471]

        数据初始化，对权重矩阵，学习率，迭代次数等进行初始化，这里考虑偏置项，权重矩阵需加一行，另外X需添加一列1用于计算偏置项，

dim = 18*9+1
w = np.zeros([dim, 1])
X = np.concatenate((np.ones([7*471, 1]), X), axis=1).astype(float)
X_test = np.concatenate((np.ones([5*471, 1]), X_test), axis=1).astype(float)
learning_rate = 1
iteration = 1000
adagrad = 0
eps = 0.0000000001
gradient = np.zeros([dim, 1])
loss = np.zeros([iteration, 1])

      参数更新，采用Adagrad优化算法，见https://blog.csdn.net/u010089444/article/details/76725843，dot函数为矩阵乘法，为了方便观察代价函数的变化，这里画出了其曲线，

for t in range(iteration):
    loss[t] = np.sum(np.power(np.dot(X, w) - y, 2))/(471*7*2)
    if t % 100 == 0:
        print(str(t) + ":" + str(loss[t]))
    gradient = np.dot(X.transpose(), np.dot(X, w) - y)/(471*7)
    adagrad += gradient ** 2
    w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
pass
m = np.arange(0, 1000, 1)
pb.plot(m, loss)
pb.show()

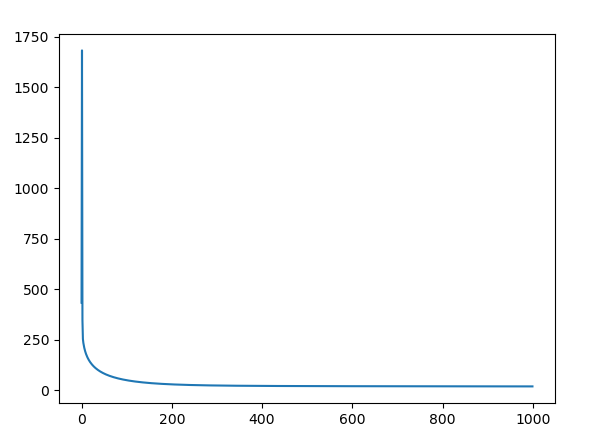
将所得权重矩阵作用在测试集上可得：