Dijkstra algorithm和Bellman-ford algorithm

Dijkstra algorithm用于算出带权的有向无环图中，从源点到其他节点的开销最小的路径。该算法包含4个步骤：

1. 找出开销最低的节点
2. 更新该节点的邻居的开销
3. 重复1和2步骤，直到对图中的每个节点都遍历到
4. 计算最终路径

例如，在下图所示的网络中，源点是u，想要计算出从u到其他节点的开销。

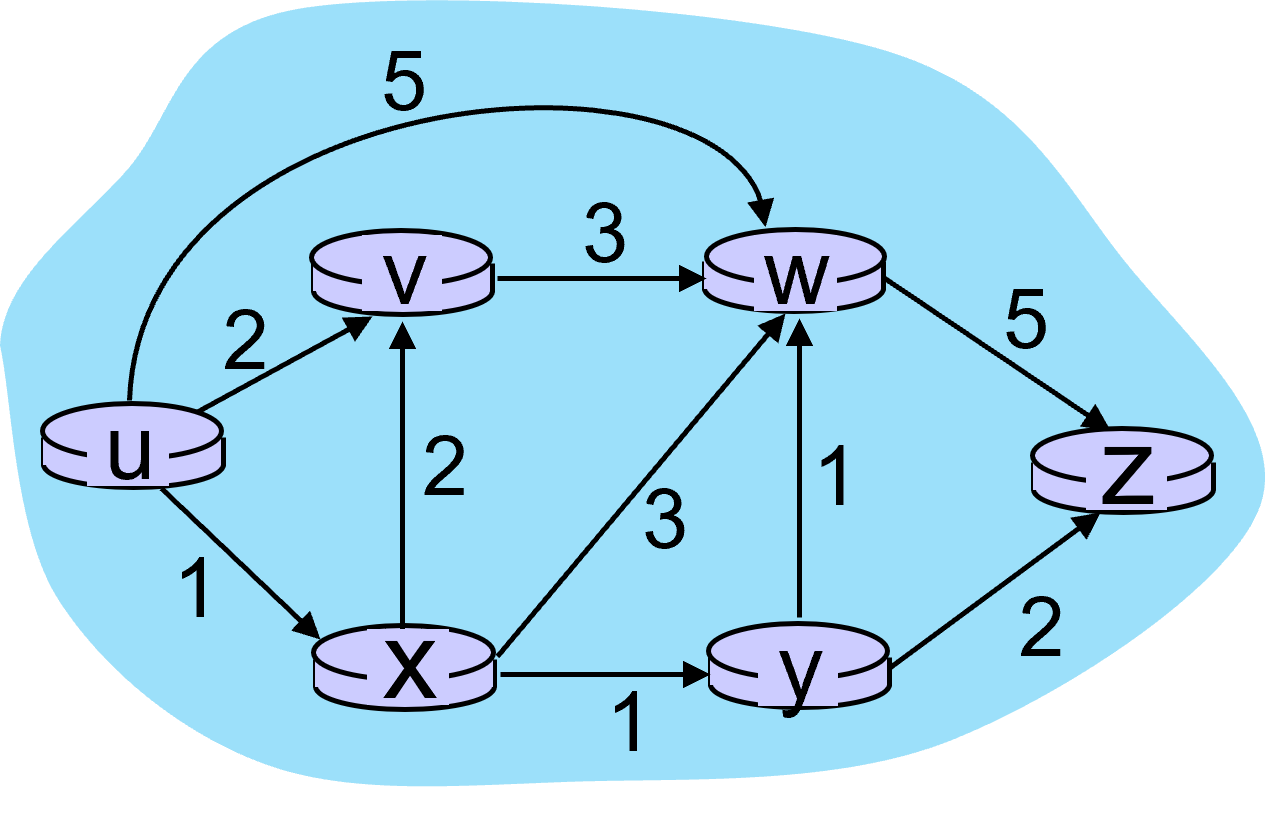
首先，更新源点u的邻居节点x,v, w的开销，得到：

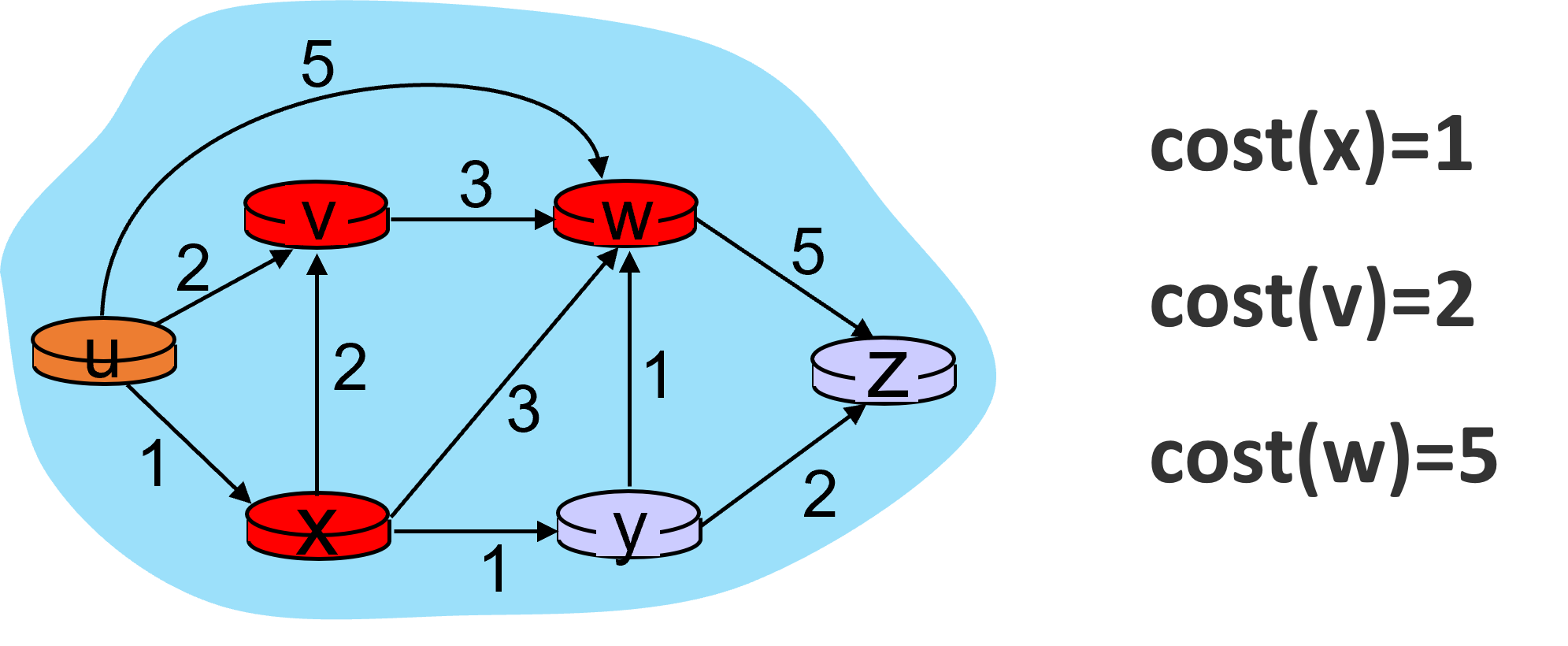
此时，开销最小的节点是x，于是更新x的邻居节点的开销，得到：

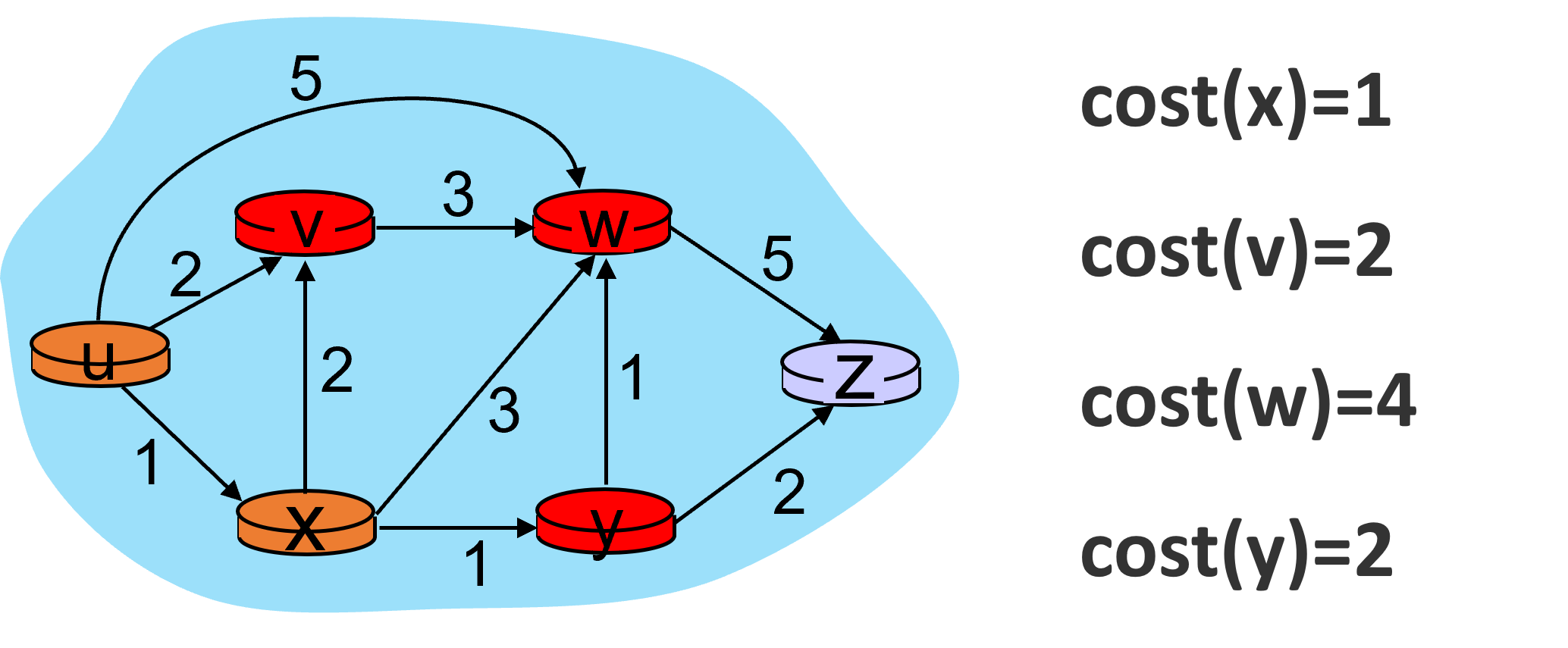
u和x节点已经处理完了，下面更新v的邻居节点的开销，得到：

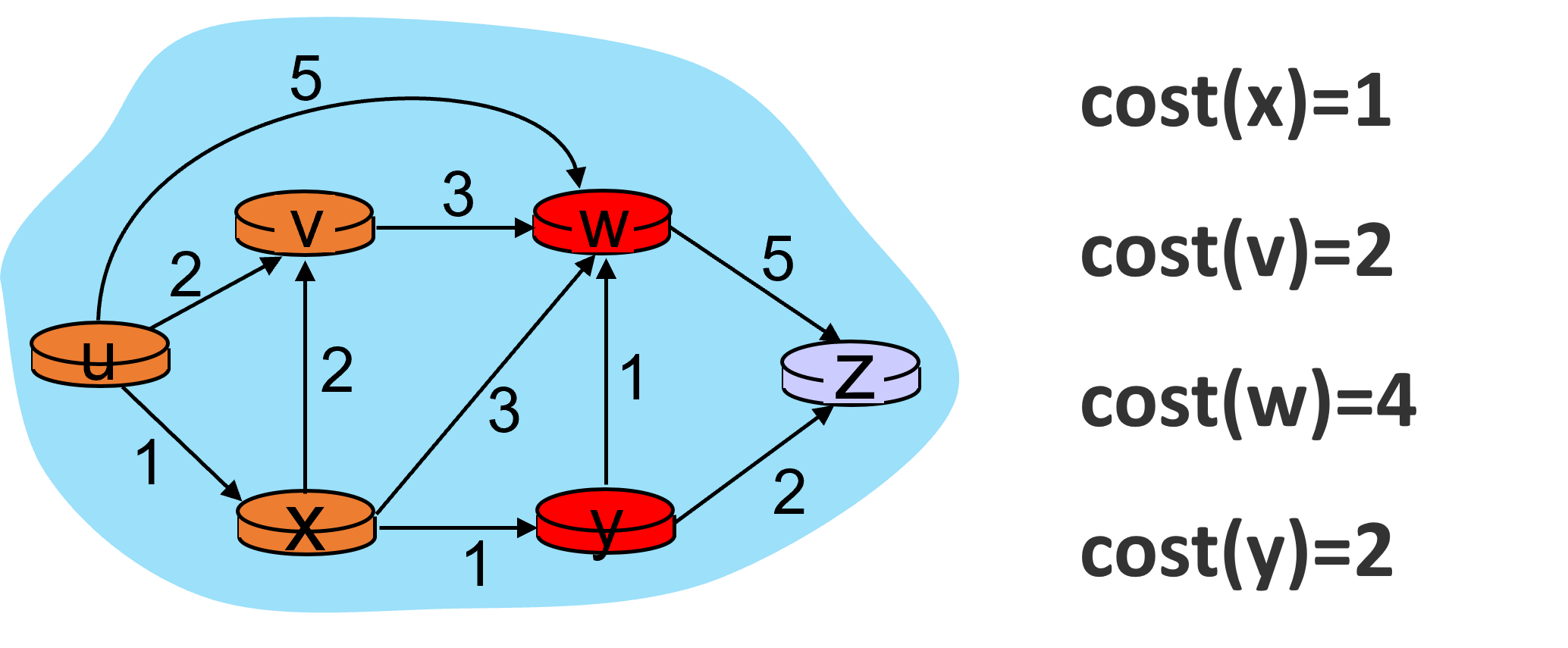
u, x, v节点均已处理完毕，下面更新y的邻居节点的开销，得到：

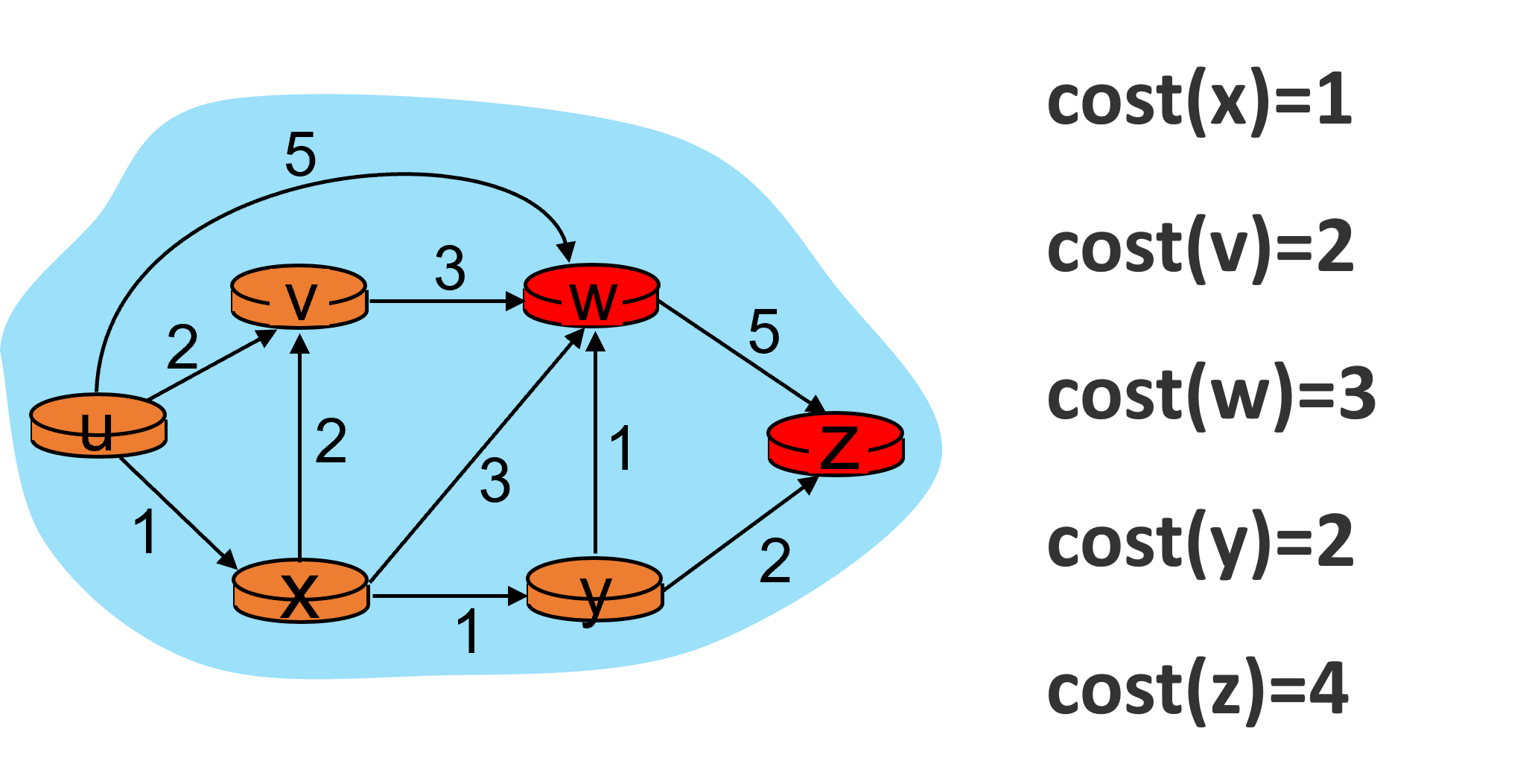
u, x, v, y节点均已处理完毕，下面更新w的邻居节点的开销，得到：

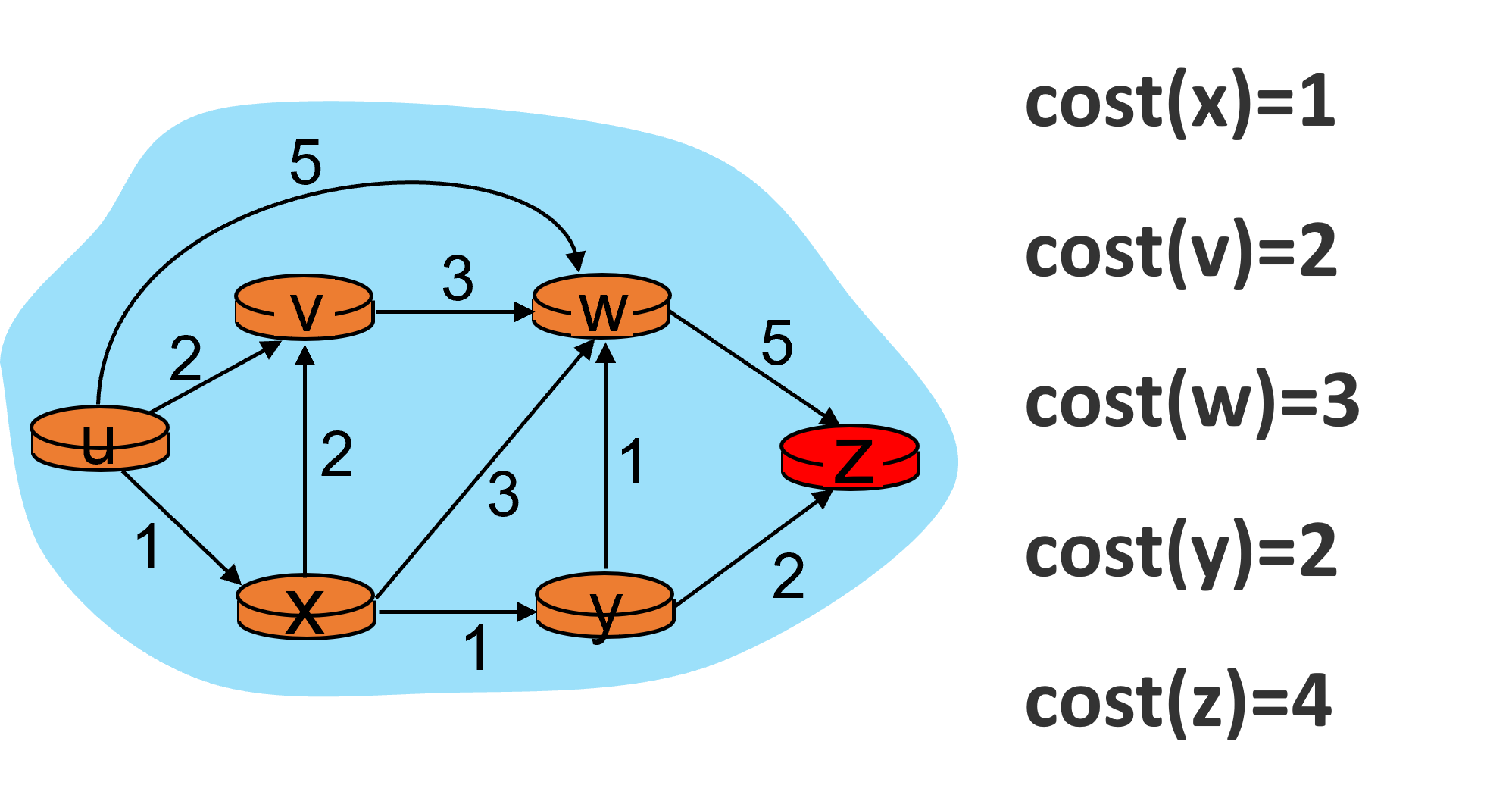
现在只剩下z节点了，它是终止节点，没有邻居节点。至此，所有的节点都已经遍历过了。

参考《算法图解》这本书，用字典表示图。用python实现Dijkstra算法的代码如下：

# 用字典构造图
graph={}
infinity=float("inf")
# 为了表示出方向和权重，这里使用字典存储节点
graph['u']={}
graph['u']['v']=2
graph['u']['x']=1
graph['u']['w']=5

graph['x']={}
graph['x']['v']=2
graph['x']['w']=3
graph['x']['y']=1

graph['v']={}
graph['v']['w']=3

graph['w']={}
graph['w']['z']=5

graph['y']={}
graph['y']['w']=1
graph['y']['z']=2

graph['z']={}

# 存储从起点到每个节点的开销
# 起点的开销为0
costs={'u':0}

# 存储到节点i的最少开销路径的父节点
parents={}

# 存储已经处理过的节点
processed=[]

# 通过for循环查询当前costs中的最少开销的节点(没有被处理过的)
def find_lowest_cost_node(costs):
    lowest_cost=infinity
    lowest_cost_node=None
    for node in costs:
        cost=costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost=cost
            lowest_cost_node=node
    return lowest_cost_node

node=find_lowest_cost_node(costs)

while node is not None:
    cost=costs[node]
    neighbors=graph[node]
    
    for n in neighbors.keys():
        new_cost=cost+neighbors[n]
        if n in costs.keys():
            if costs[n] > new_cost:
                costs[n]=new_cost
                parents[n]=node
        else:
            costs[n]=new_cost
            parents[n]=node
    processed.append(node)
    node=find_lowest_cost_node(costs)

print(costs)

 

Dijkstra算法中每个节点只遍历一次，因此它无法处理有负权边的图。例如在下图中，会先处理v节点，得到cost(v)=2，然后再处理x节点，得到cost(x)=3。v是x的邻居节点，此时会得到cost(v)=1。然而由于v节点已经被遍历过了，所以这时无法接受其开销的更改。

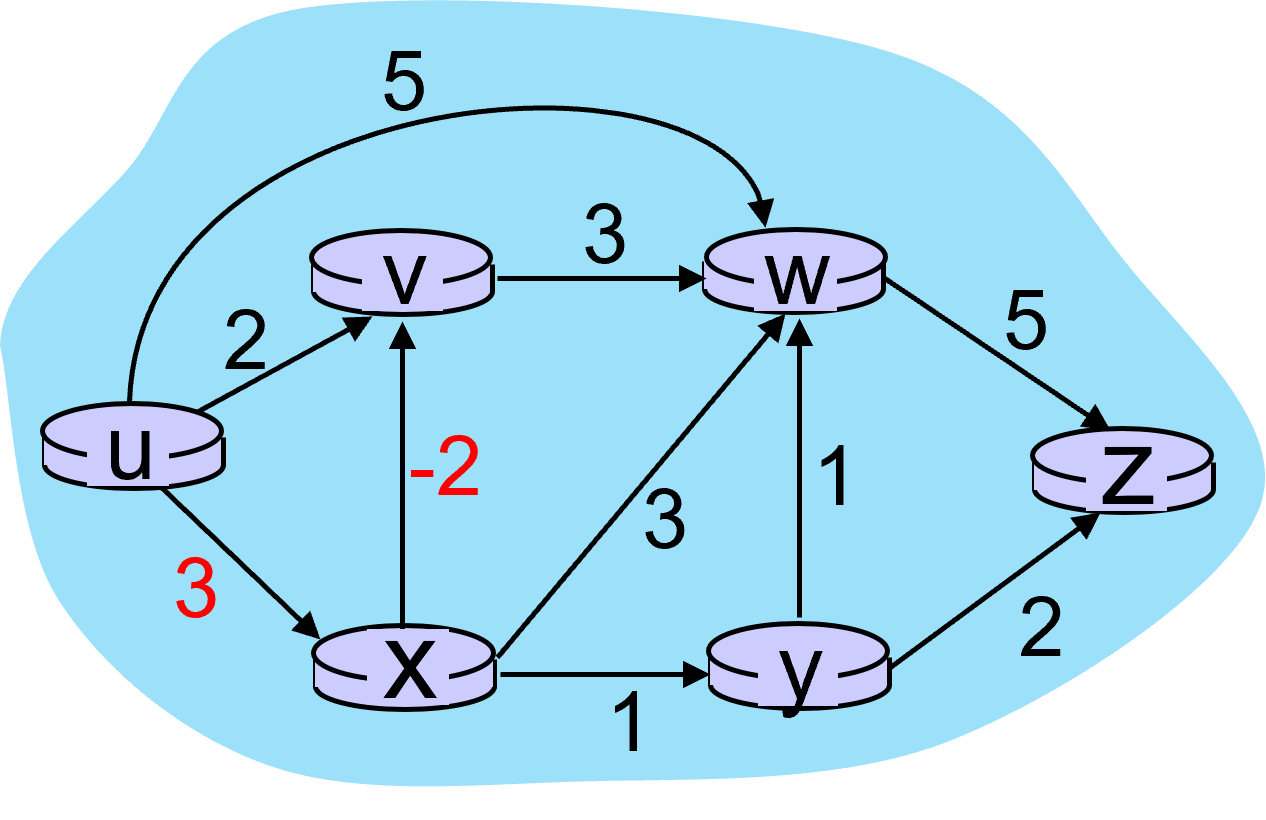
对此情况，可使用Bellman-ford算法。本质就是让v节点能够再被处理一次。

处理u节点

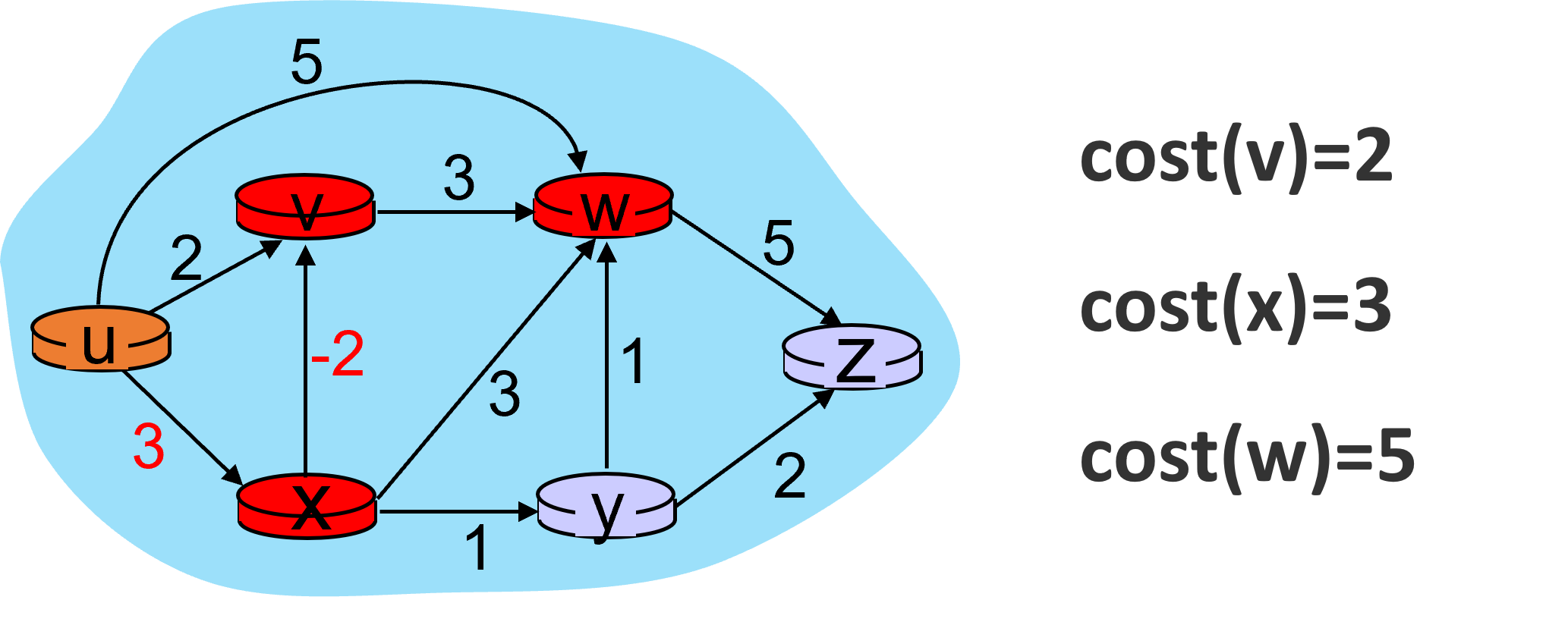
处理v节点，此时不需要优先处理开销最低的节点。

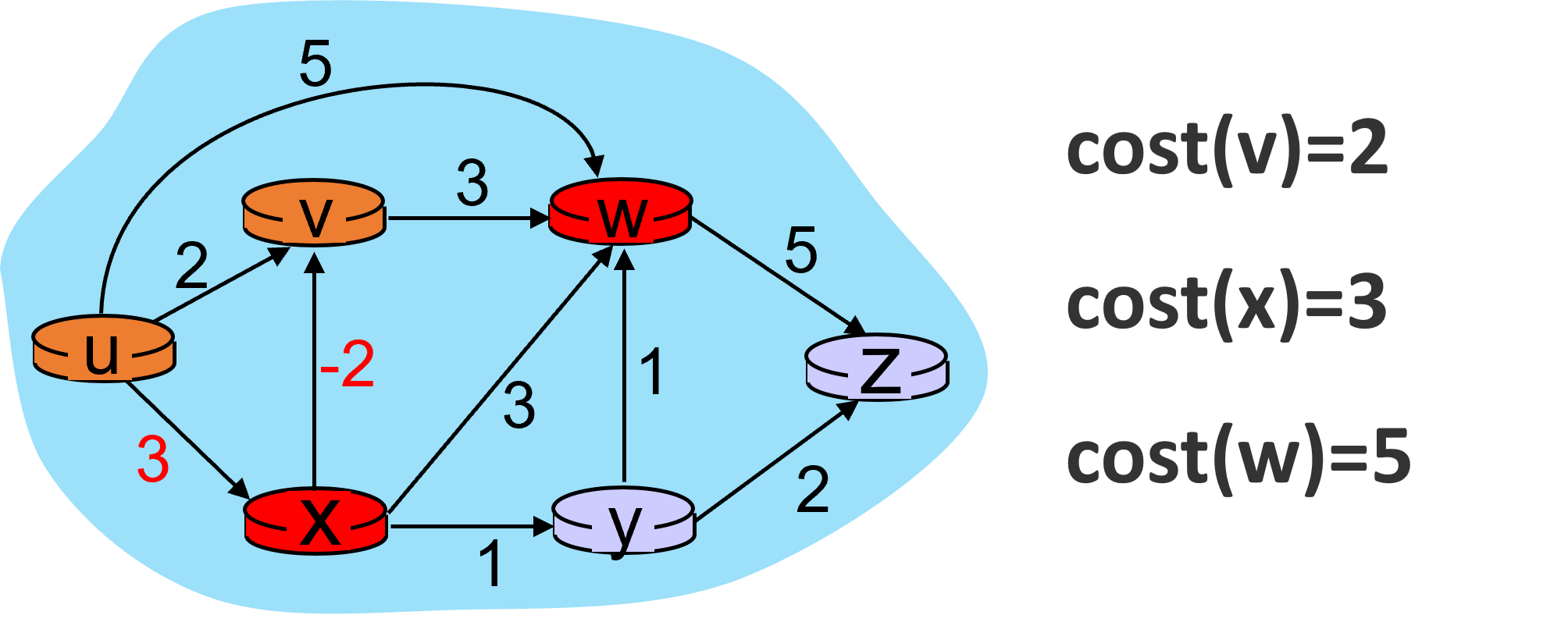
处理x节点，此时v的开销发生了变化。

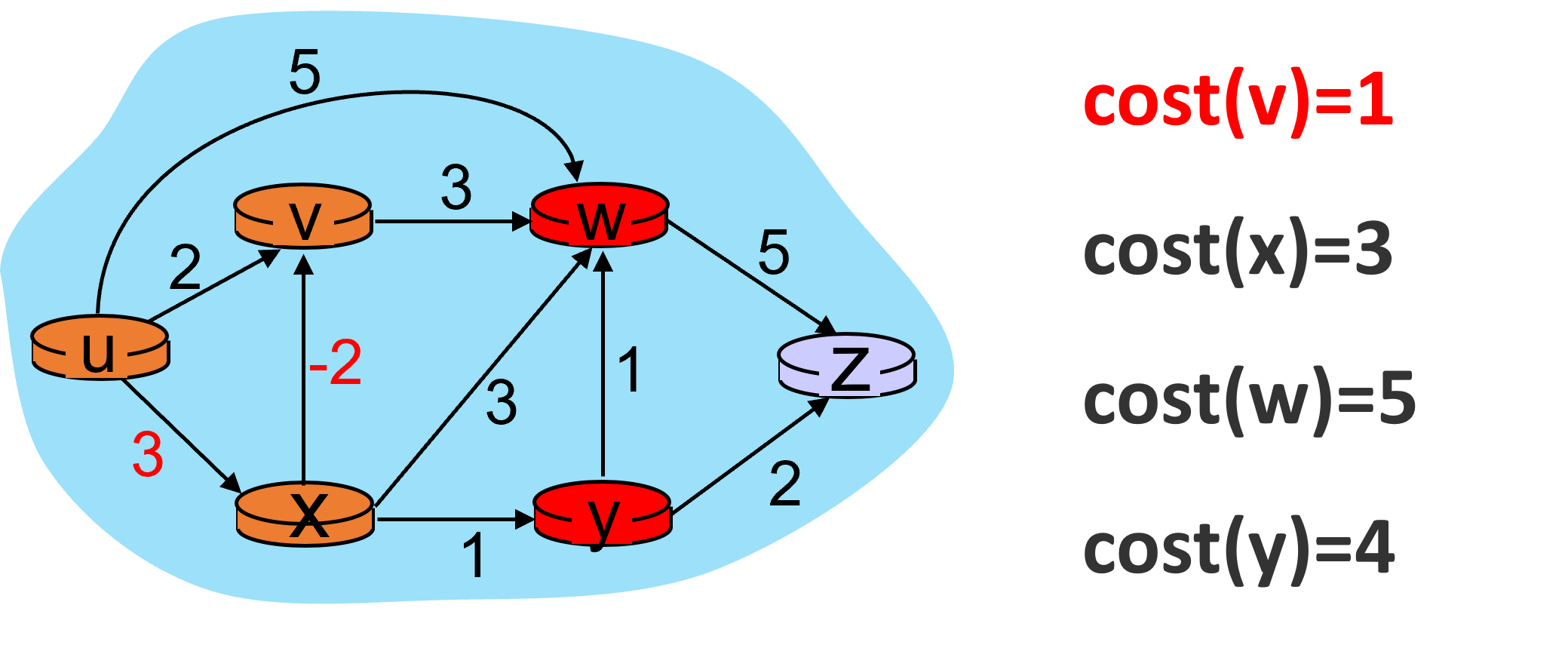
处理w节点

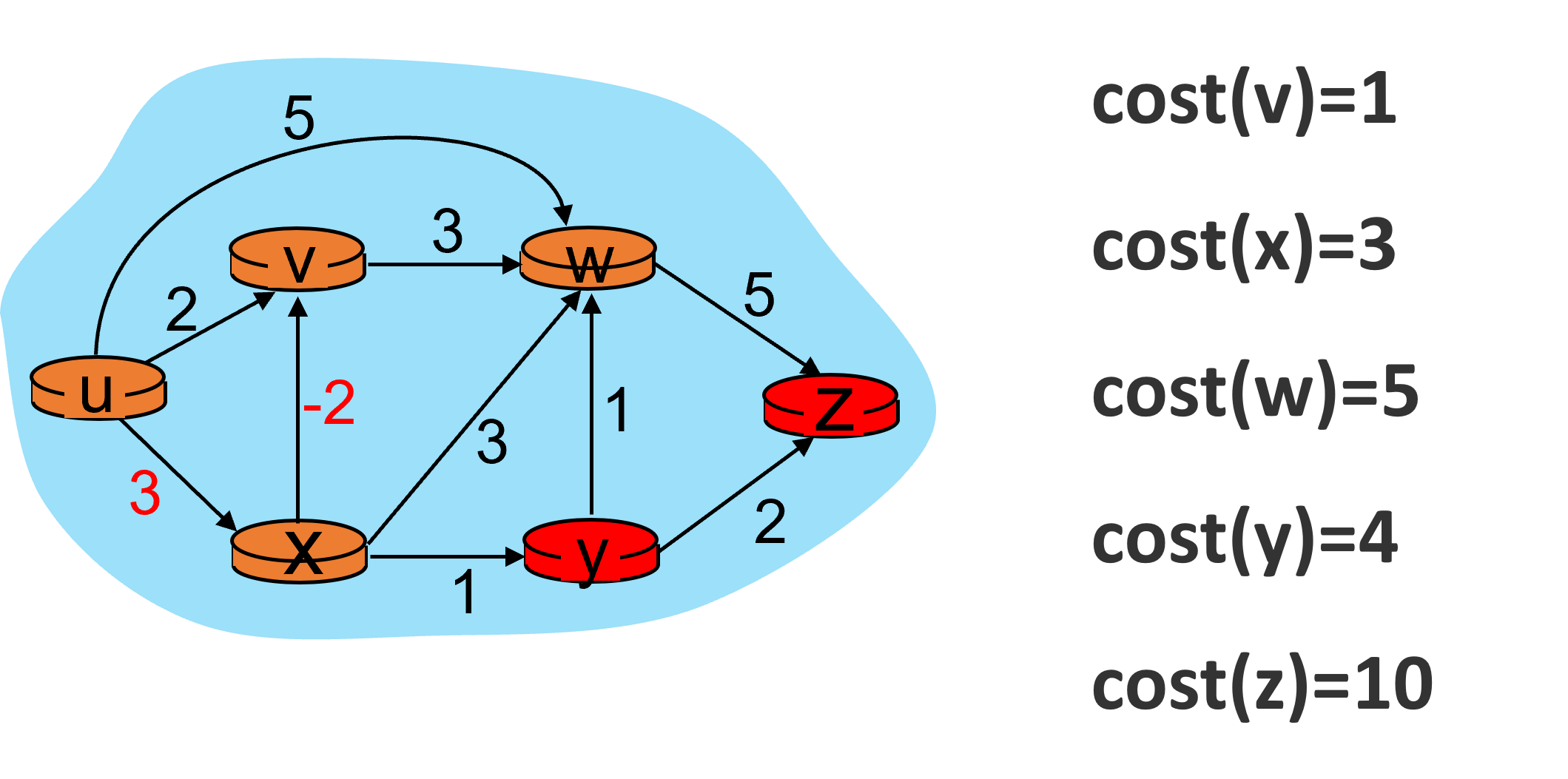
处理y节点

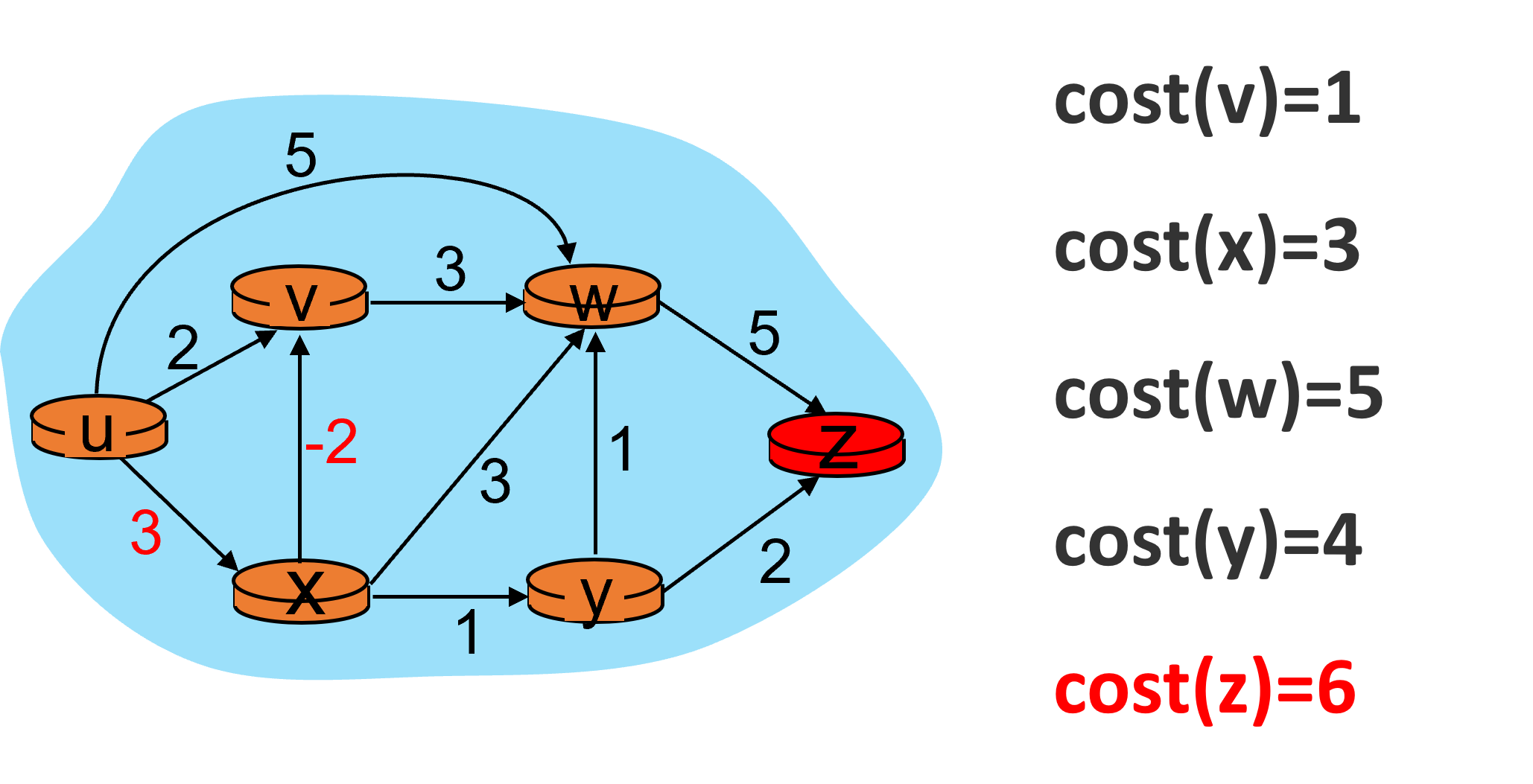
最后再处理z节点。z节点没有邻居节点。

在第一次遍历的过程中，节点v和z的开销发生了变化。这可能会引起其他节点开销的改变。于是遍历一下这两个节点。

首先是v节点，它开销的变化导致w节点的开销也变化了。

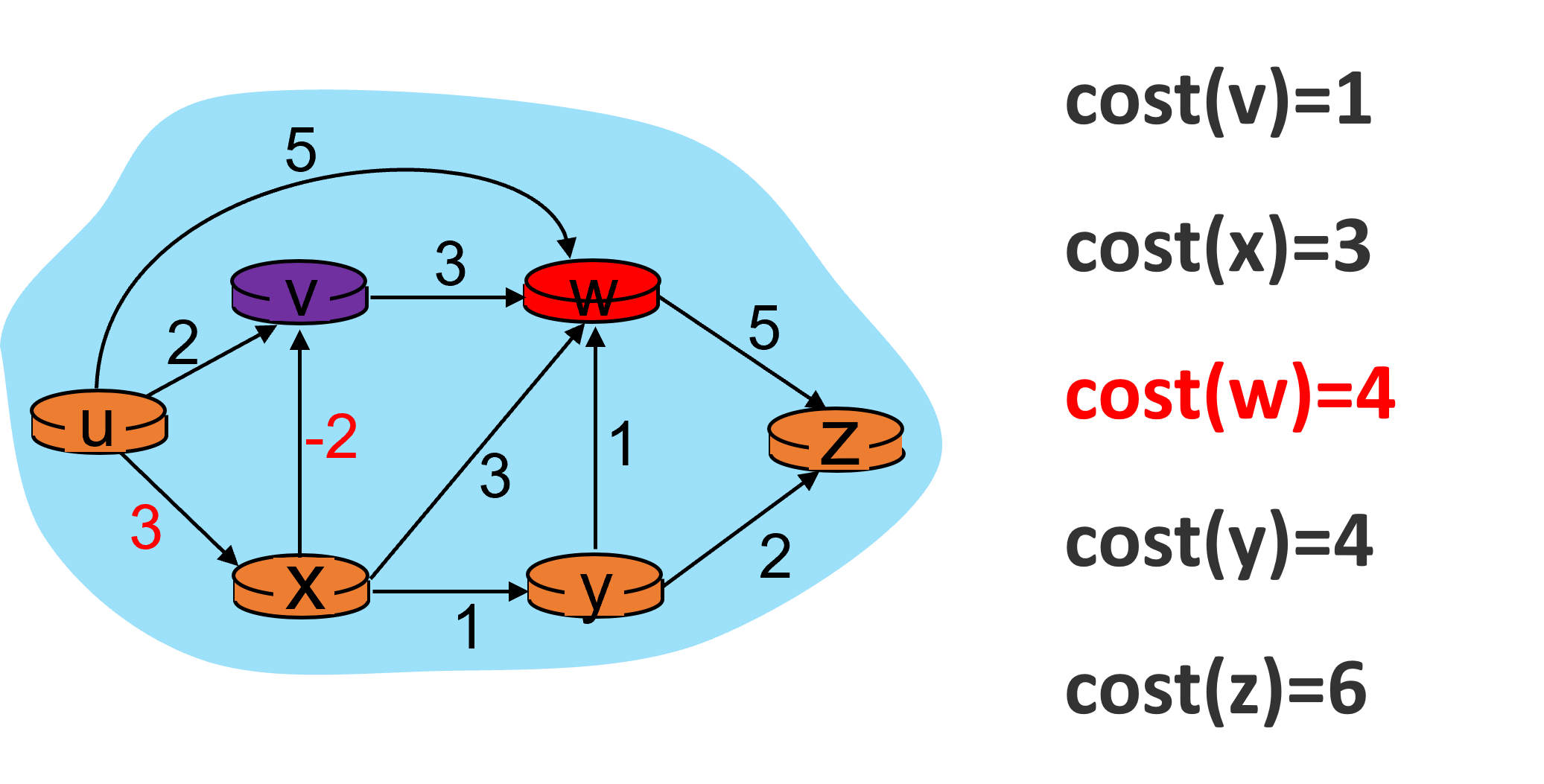
然后是z节点，但是由于它没有邻居节点，因此没有影响。第二次迭代结束。由于本次迭代中，w节点的开销发生了变化，所以需要第三次迭代。

如下图所示，在第三次迭代中，没有任何节点的开销发生变化。此时可以结束迭代了。

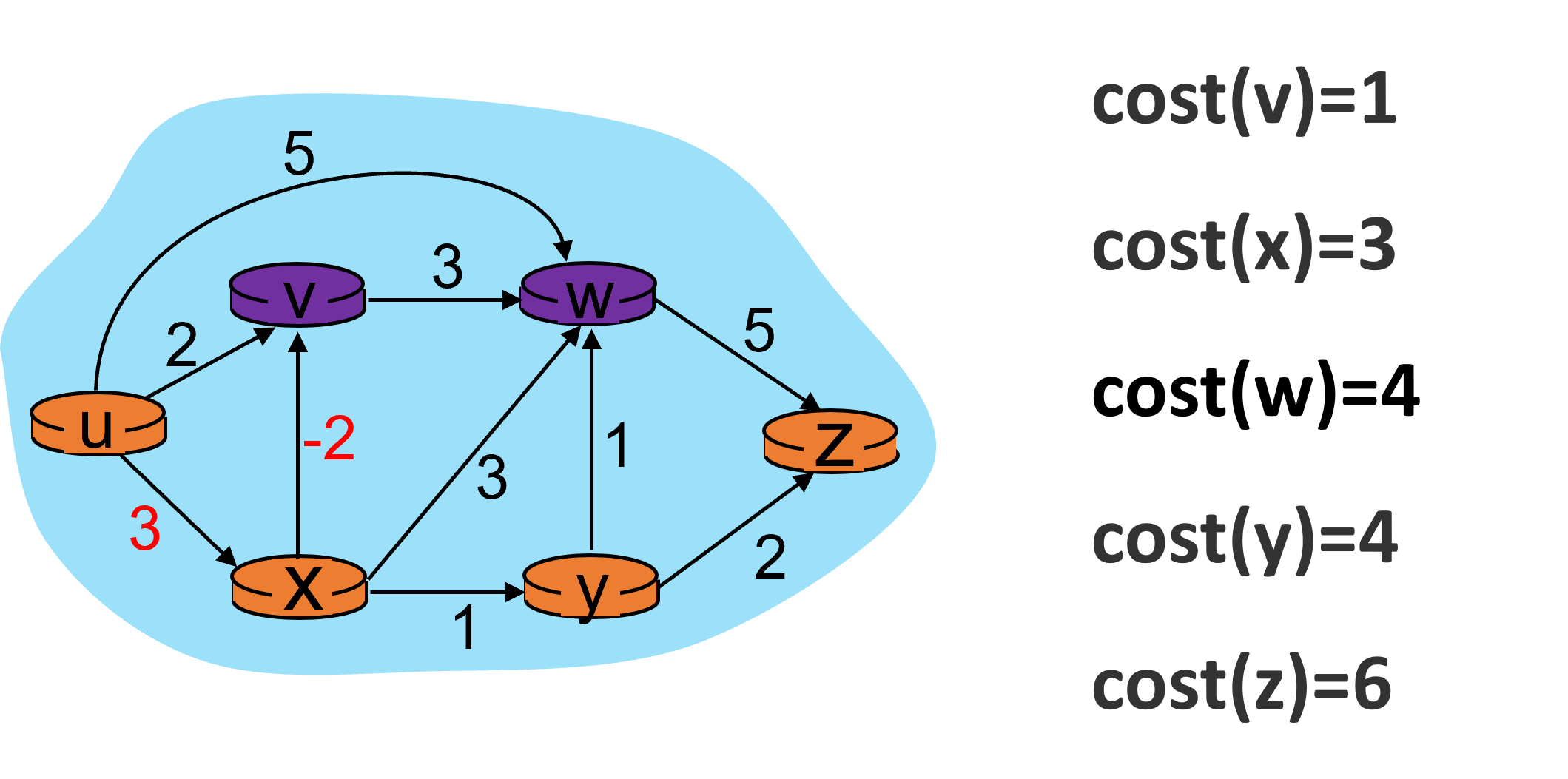
对于由V个节点组成的图，两个节点之间的最短路径，最多只能包含V-1条边。因此最多迭代V-1次就应该结束了。如果迭代次数大于V-1，就说明图中存在负权边。

看个有负权边的例子。下图中x -> v -> w和y -> w -> x构成了两个负权环。

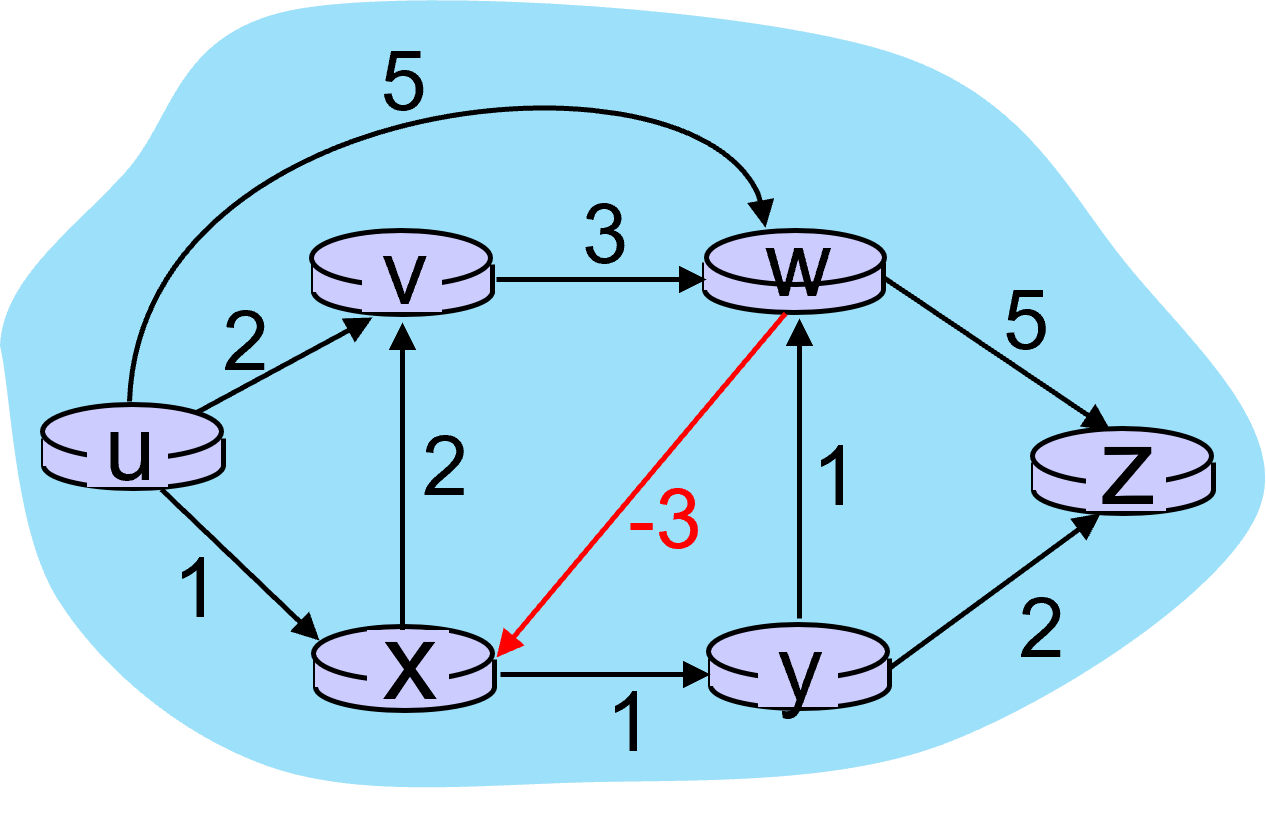
第一次迭代的过程如下图所示。

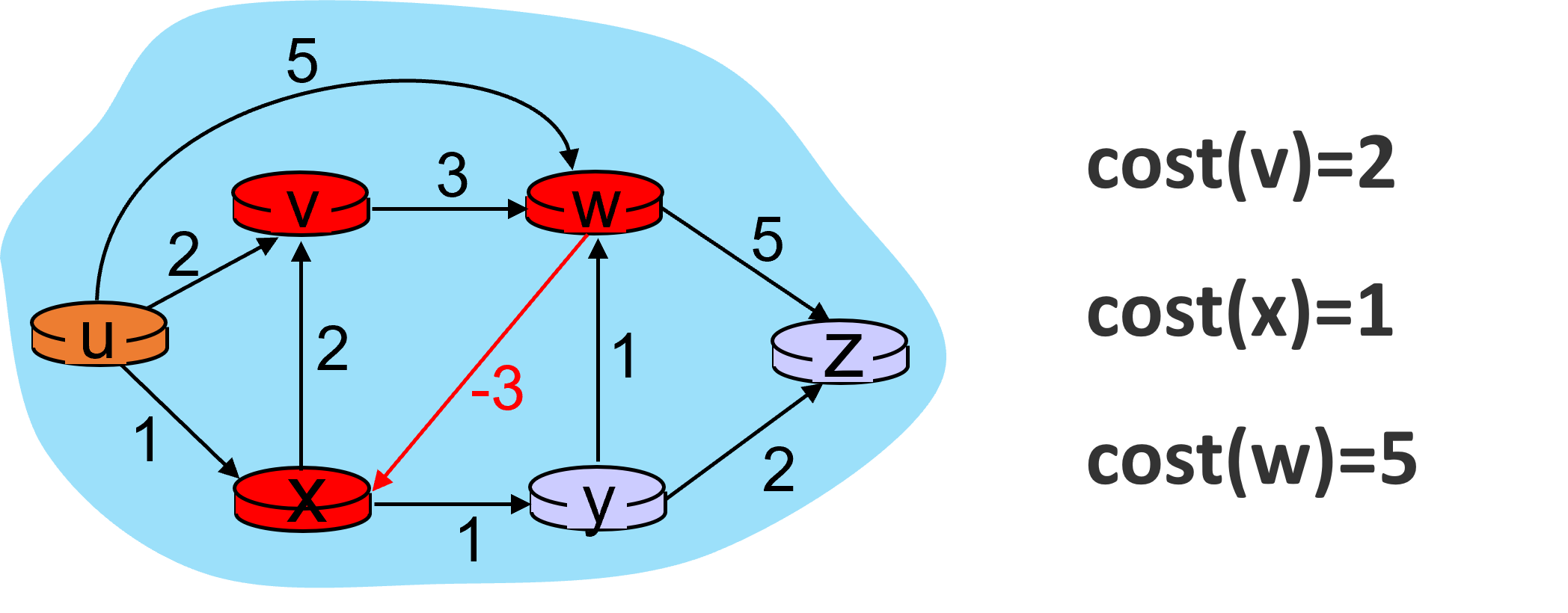
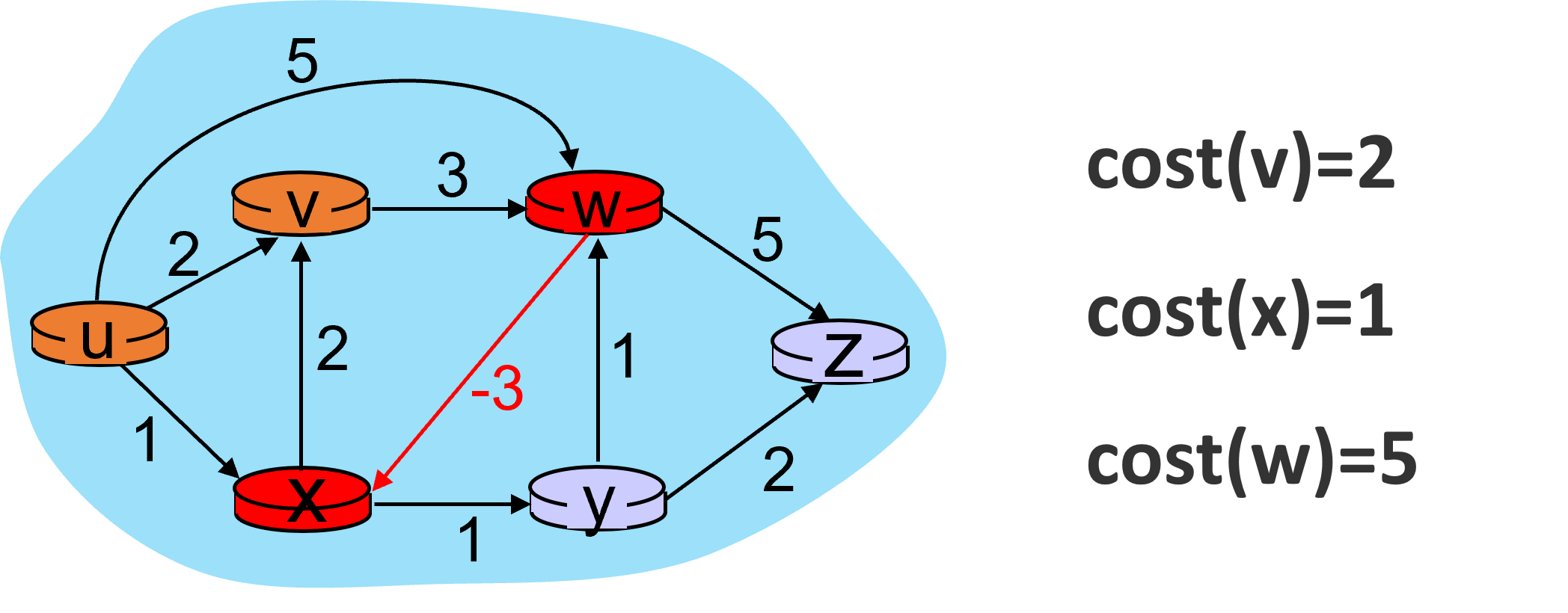
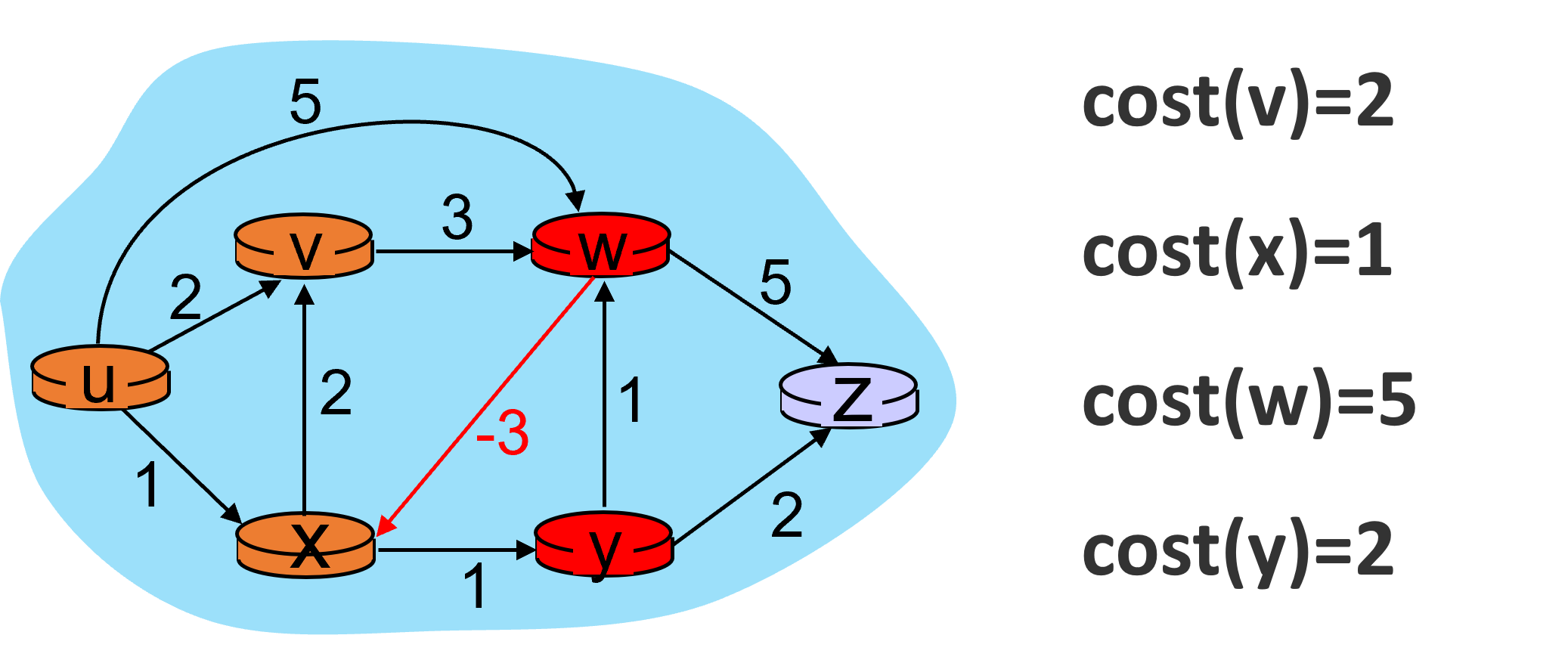
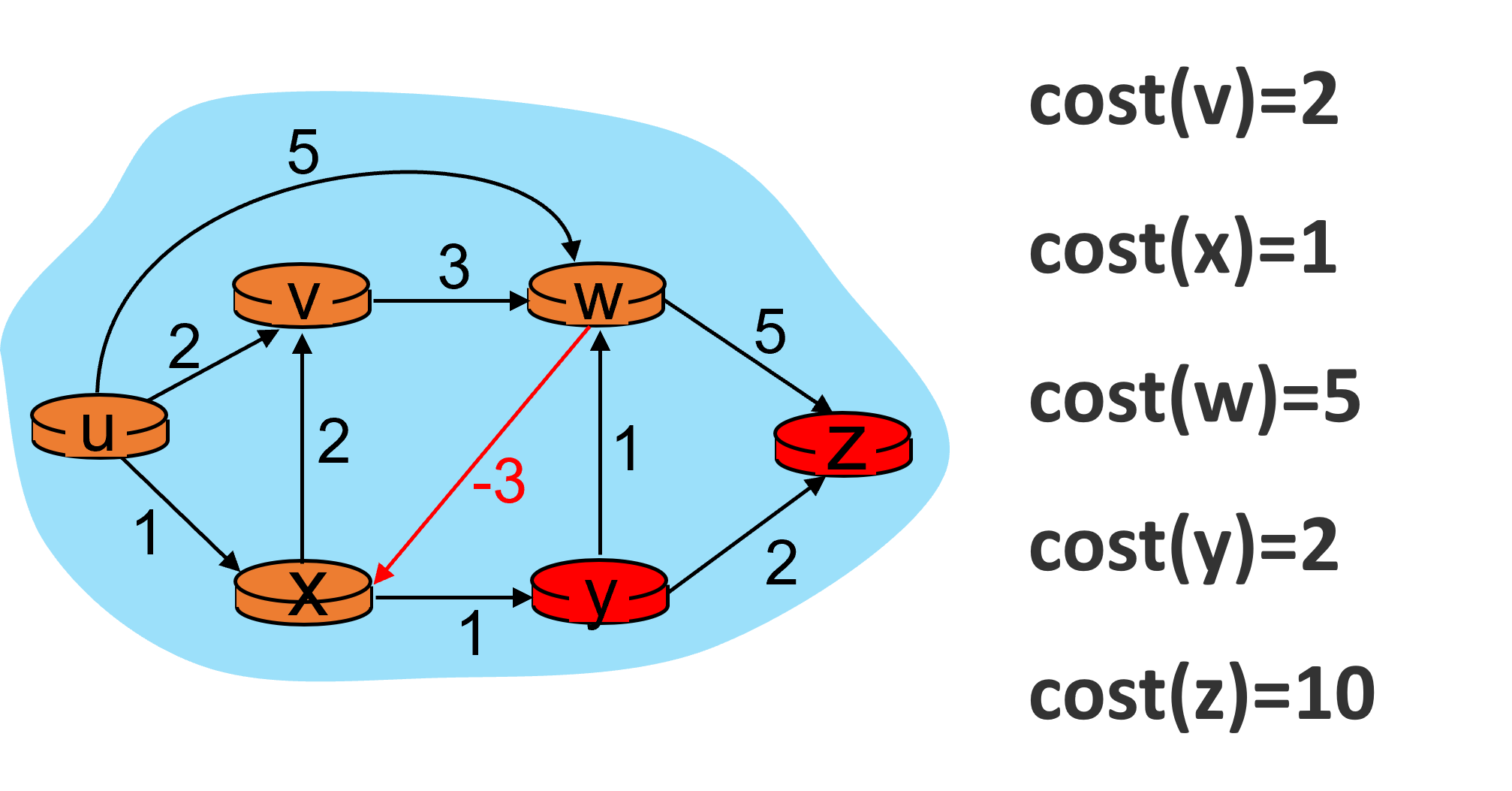
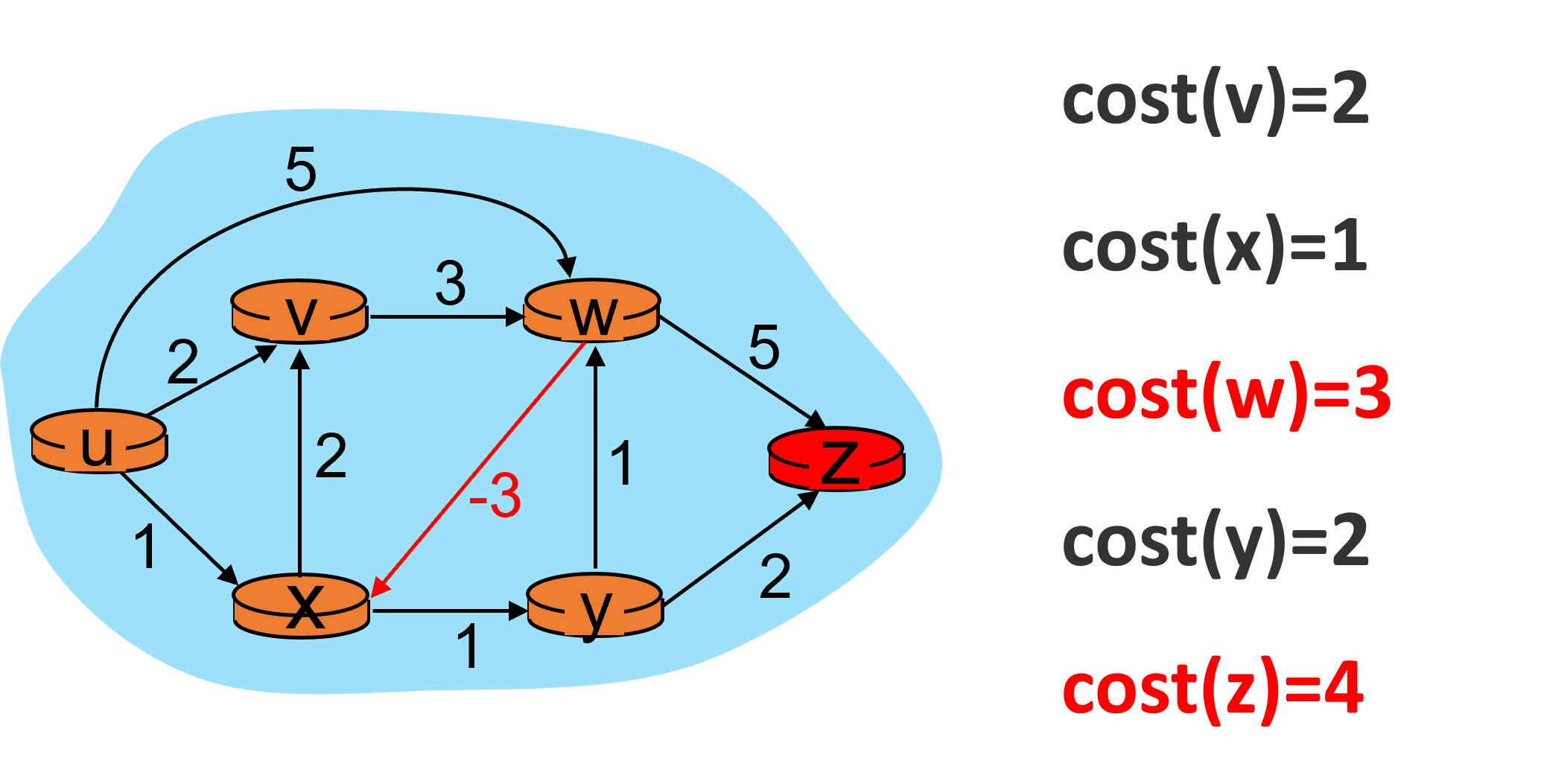
第一次迭代结束。在此过程中，w节点的开销发生了改变，于是需要第二次迭代。

此时，w节点开销的改变引起了x节点开销的变化，为0。

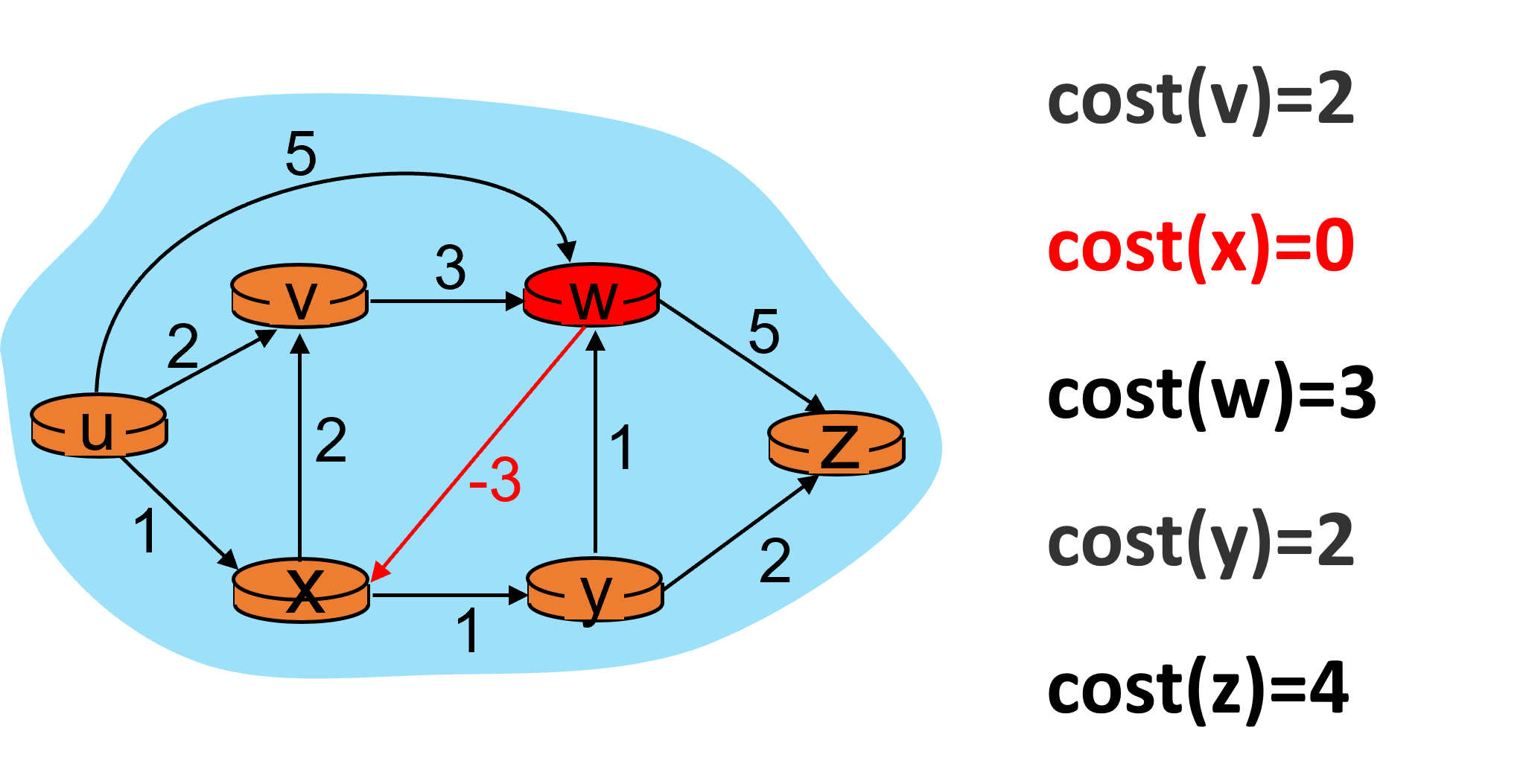
继续进入下一次迭代。x节点开销的改变引起了y节点开销的变化。

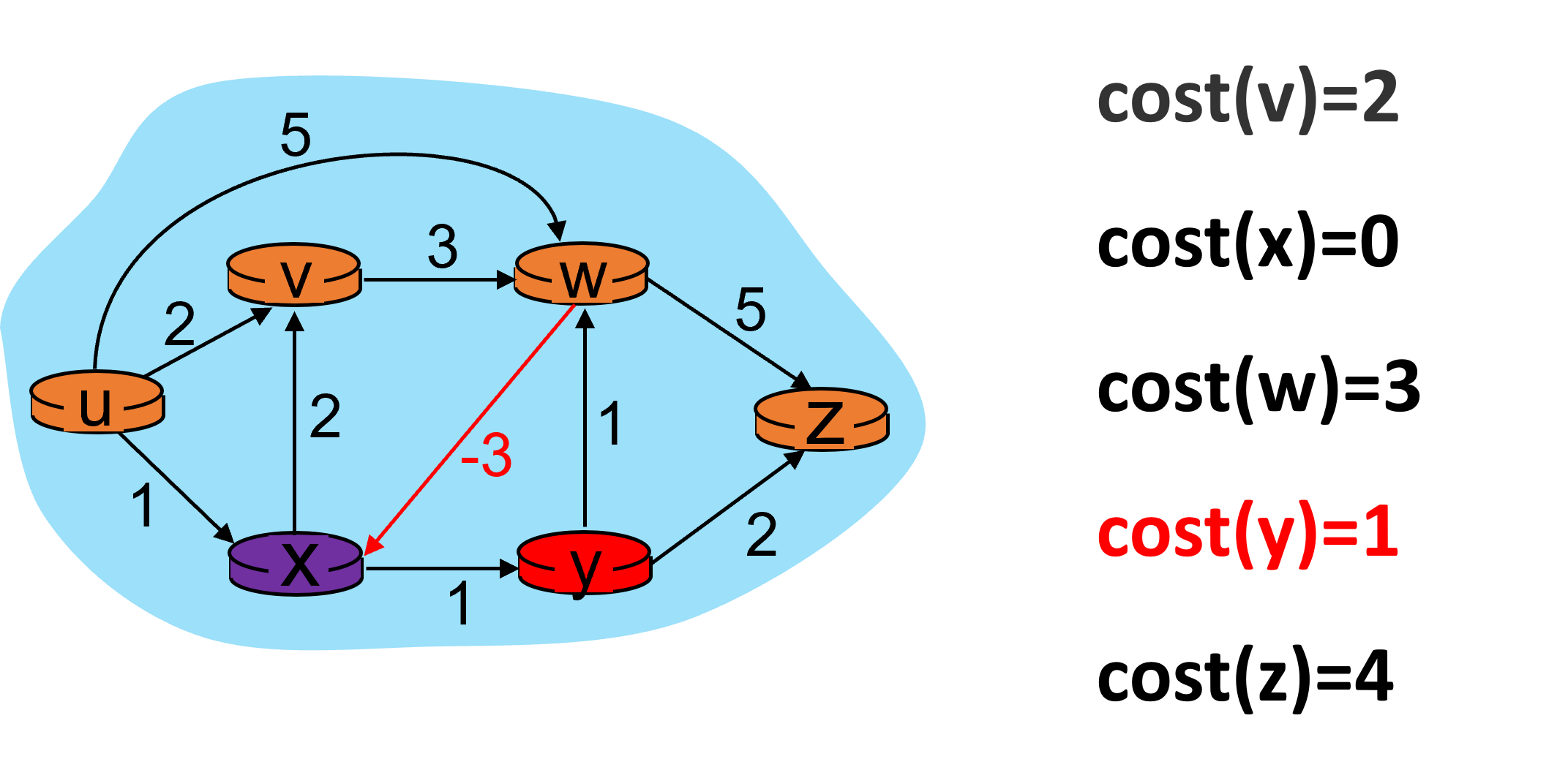
继续进入下一次迭代。y节点开销的改变引起了w和z节点开销的变化。

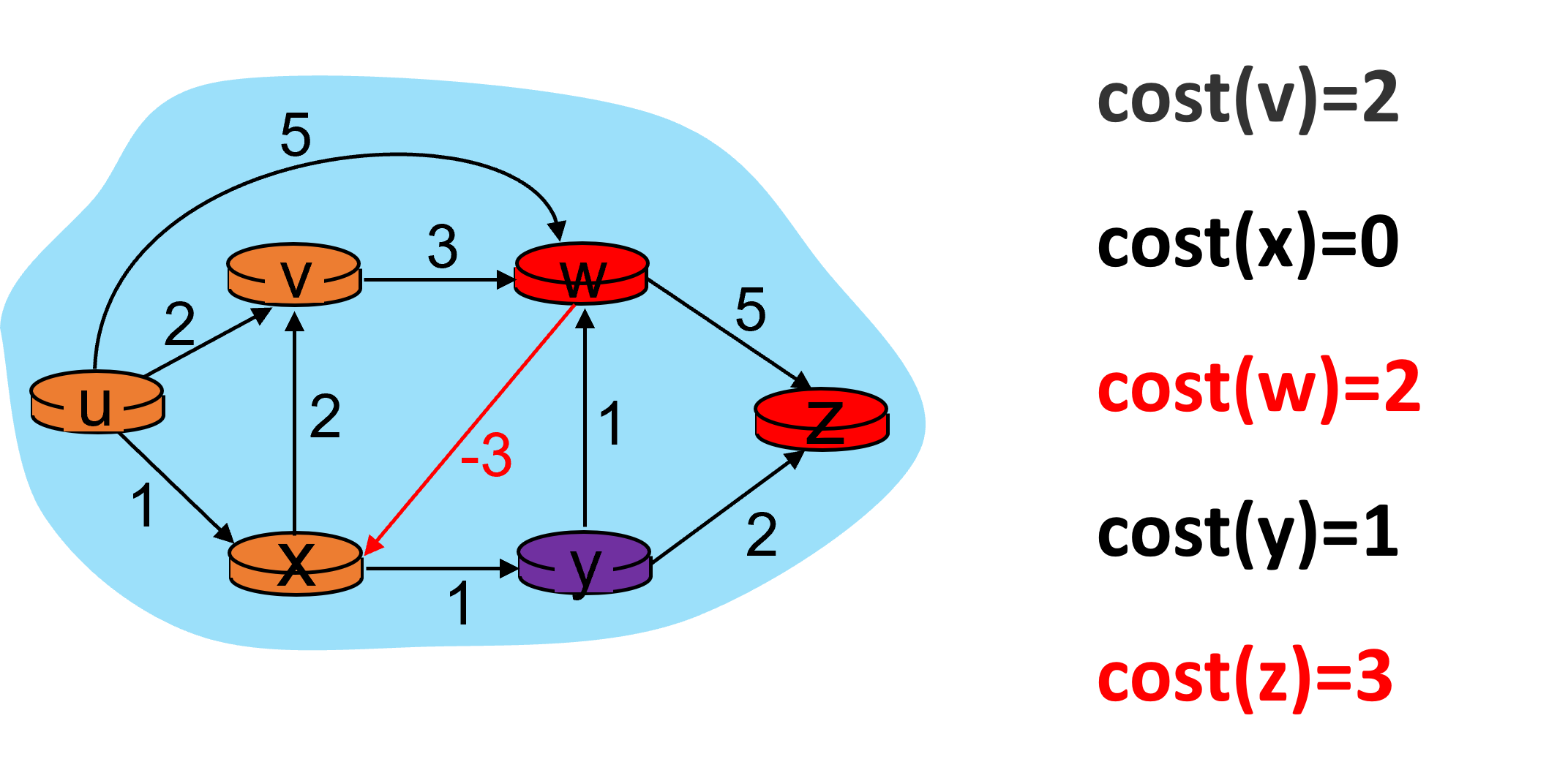
至此，已经能够发现如果存在负权环，可能会导致开销无限循环地减少的情况。Bellman-ford算法会报告负权环的存在，但不会尝试进一步计算从源点到各顶点的有效路径，因为此时的路径值不稳定。

根据GPT和其他博客所讲，Bellman-ford算法的标准化实现是在一个长度为V-1的for循环中，遍历图中的所有节点，python代码如下：

graph={}
infinity=float("inf")
# 为了表示出方向和权重，这里使用字典存储节点
graph['u']={}
graph['u']['v']=2
graph['u']['x']=1
graph['u']['w']=5

graph['v']={}
graph['v']['w']=3

graph['x']={}
graph['x']['v']=2
# graph['x']['w']=3
graph['x']['y']=1

graph['w']={}
graph['w']['z']=5
graph['w']['x']=-3

graph['y']={}
graph['y']['w']=1
graph['y']['z']=2

graph['z']={}

V=list(graph.keys())

parents={}
costs={v:infinity for v in V}
costs['u']=0

for i in range(len(V)-1):
    for node in V:
        cost=costs[node]
        neighbors=graph[node]
        for n in neighbors.keys():
            new_cost=cost+neighbors[n]
            if new_cost < costs[n]:
                costs[n]=new_cost
                parents[n]=node

# 检测负权环
for node in V:
    cost=costs[node]
    neighbors=graph[node]

    for n in neighbors.keys():
        if cost+neighbors[n] < costs[n]:
            print("Graph contains a negative weight cycle")
            break

print(costs)
print(parents)

 

但是我觉得没有必要在每次迭代中，都把V中的节点全部遍历，每次只需要遍历开销发生变化的节点就可以了。所以下面的代码，我用队列存每次迭代过程中开销发生变化的节点。如果某次迭代，没有开销发生变化的节点，则终止迭代。

 

from collections import deque

graph={}
infinity=float("inf")
# 为了表示出方向和权重，这里使用字典存储节点
graph['u']={}
graph['u']['v']=2
graph['u']['x']=1
graph['u']['w']=5

graph['v']={}
graph['v']['w']=3

graph['x']={}
graph['x']['v']=2
# graph['x']['w']=3
graph['x']['y']=1

graph['w']={}
graph['w']['z']=5
graph['w']['x']=-3

graph['y']={}
graph['y']['w']=1
graph['y']['z']=2

graph['z']={}

V=list(graph.keys())

parents={}
costs={}

for i in range(len(V)):
    costs[V[i]]=infinity

costs['u']=0

nodeQueue=deque(V)
tmpQueue=deque()

count=len(V)-1

while nodeQueue and count:
    node=nodeQueue.popleft()
    cost=costs[node]
    neighbors=graph[node]

    for n in neighbors.keys():
        new_cost=cost+neighbors[n]

        if new_cost < costs[n]:
            costs[n]=new_cost
            parents[n]=node
            tmpQueue.append(n)
    if not nodeQueue:
        nodeQueue=tmpQueue
        tmpQueue.clear()
        count-=1


for node in V:
    cost=costs[node]
    neighbors=graph[node]

    for n in neighbors.keys():
        if cost+neighbors[n] < costs[n]:
            print("Graph contains a negative weight cycle")
            break

print(costs)