matlab FFT -2020
matlab FFT 横纵坐标
matlab FFT 横坐标问题
我们知道Fourier分析是信号处理里很重要的技术,matlab提供了强大的信号处理能力,但是有一些细节部分需要我们注意。
记信号f(t)的起始时间为t_start, 终止时间为t_end, 采样周期为Ts, 可以计算信号的持续时间Duration=t_end – t_start,
信号离散化造成的采样点数:N = Duration/Ts + 1;
根据Fourier分析的相关结论,我们知道时域的采样将会造成频域的周期化,该周期为采样频率Fs(著名的香农采样定理基于此).于是,经过matlab的fft函数处理后,得到数据的横坐标为0:Fs/(N-1):Fs。相关代码如下所示:
%零频率分量移到坐标中心的傅里叶变换
Ts = 0.01;
t_start = 0.5; t_end = 5;
t = t_start:Ts:t_end;
y = 0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
Duration = t_end - t_start;
N = Duration/Ts + 1; %采样点数
Fs = 1/Ts;
f_x = 0:Fs/(N-1):Fs;
y_f = fft(y);
subplot(3,1,1); plot(t,y); title('original signal');
subplot(3,1,2);plot(f_x,abs(y_f)); title('fft transform');
subplot(3,1,3);plot(f_x-Fs/2,abs(fftshift(y_f))); title('shift fft transform');
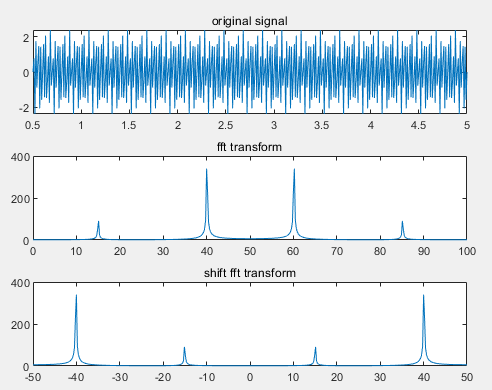
也就是说,如果我们不使用fftshift,其变换后的横坐标为0:Fs/(N-1):Fs,如果使用fftshift命令,0频率分量将会移到坐标中心,这也正是matlab中帮助中心给出的意思:对fft的坐标进行了处理。实际上由于频谱的周期性,我们这样做是合理的,可以接受的。
请读者特别要注意横坐标的差别。另外,根据函数的特性,频谱应当只有在15Hz,40Hz出现峰值,但是fft变换后在60Hz,及85Hz处同样出现了峰值,应当可以从fft的计算过程中得到相应的解释。事实上,如果我们用15Hz,60Hz来测试fft变换,也即是:y = 0.5*sin(2*pi*15*t)+2*sin(2*pi*60*t);图像如下所示,没有任何变化。
这种现象提醒我们,频率在Fs以内,即 0<f<Fs,f 以及 Fs–f都有可能是测试信号的频率谱,这就给我们带来了歧义。并且从第三个子图也可以看出,这时候的fftshift会给我们带来错误的引导,也就是说,如果我们试图采样fft或者fftshift来分析信号的频率谱显得不那么靠谱了,matlab的fft谱线与信号的实际频率并不是一一对应的映射关系。这当然不是我们所期望看到的结果,所以实际分析信号时,有关这个问题需要额外的注意。
实际上,这也就间接地证明了Nyquist采样定理的合理性:采样频率要高于截止频率的两倍,上面的处理中我们所使用的采样频率为100Hz,于是当截止频率超过50Hz时,就会出现混叠效应,特殊情况就如上图所示:完全一样。于是,这也就告诉我们若要正确的显示频谱,需要仔细地考量采样频率与截止频率的关系,若太小,则有可能出现混叠,若太大,则计算代价过高。
上面内容说明了fft横坐标与采样定理的问题,下面我总结了坐标问题如下:
1)如果你用fft计算振幅谱,且fft变换后的点数为N的话,只用fft,而不用fftshift,那么:你只需要显示fft变换结果的前N/2个点,横坐标为:
f=index*Fs/(N-1),index=0:N/2-1 ;
2)如果你用fft计算振幅谱,且fft变换后的点数为N的话,用了fft,还用了fftshift,那么:你需要显示fft变换结果的数据点,横坐标为:
f = 0:Fs/(N-1):Fs; f=f-Fs/2;
原因:对实信号fft,产生了负频率,由于FFT变化是对称的,所以负频率对应到了Fs/2~Fs上,对实信号而言,该段频率没有任何意义,所以只显示到Fs/2。
matlab FFT 纵坐标问题
一.调用方法
X=FFT(x);
X=FFT(x,N);
x=IFFT(X);
x=IFFT(X,N);
用MATLAB进行谱分析时注意:
(1)函数FFT返回值的数据结构具有对称性。
例:
N=8;
n=0:N-1;
xn=[4 3 2 6 7 8 9 0];
Xk=fft(xn)
Xk =
39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i
Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例
例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;
fs=100;N=128; %采样频率和数据点数
n=0:N-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号
y=fft(x,N); %对信号进行快速Fourier变换
mag=abs(y); %求得Fourier变换后的振幅
f=n*fs/N; %频率序列
subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;
subplot(2,2,2),
plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;
%对信号采样数据为1024点的处理
fs=100;N=1024;n=0:N-1;t=n/fs;
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号
y=fft(x,N); %对信号进行快速Fourier变换
mag=abs(y); %求取Fourier变换的振幅
f=n*fs/N;
subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;
subplot(2,2,4);
plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅
xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;
运行结果:
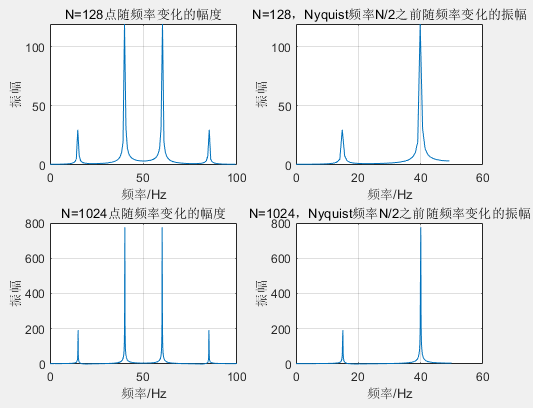
fs=100Hz,Nyquist频率为fs/2=50Hz。整个频谱图是以Nyquist频率为对称轴的。并且可以明显识别出信号中含有两种频率成分:15Hz和40Hz。由此可以知道FFT变换数据的对称性。因此用FFT对信号做谱分析,只需考察0~Nyquist频率范围内的幅频特性。若没有给出采样频率和采样间隔,则分析通常对归一化频率0~1进行。另外,振幅的大小与所用采样点数有关,采用128点和1024点的相同频率的振幅是有不同的表现值,但在同一幅图中,40Hz与15Hz振动幅值之比均为4:1,与真实振幅0.5:2是一致的。为了与真实振幅对应,需要将变换后结果乘以2除以N。
例2:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t),fs=100Hz,绘制:
1)数据个数Ndata=32,FFT所用的采样点数NFFT=32;
(2)Ndata=32,NFFT=128;
(3)Ndata=136,NFFT=128;
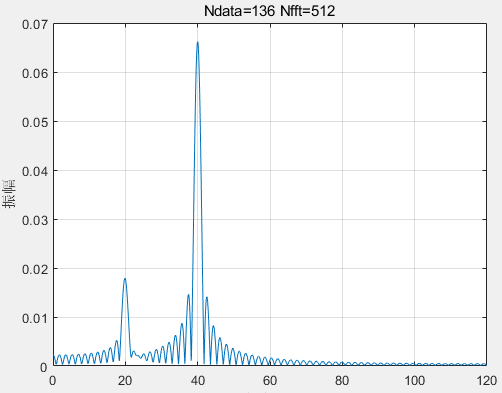
(4)Ndata=136,NFFT=512。
fs=100; %采样频率
Ndata=32; %数据长度
N=32; %FFT的数据长度
n=0:Ndata-1;t=n/fs; %数据对应的时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %时间域信号
y=fft(x,N); %信号的Fourier变换
mag=abs(y); %求取振幅
f=(0:N-1)*fs/N; %真实频率
figure
subplot(2,2,1),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅'); title('Ndata=32 Nfft=32');grid on;
Ndata=32; %数据个数
N=128;%FFT所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅'); title('Ndata=32 Nfft=128');grid on;
Ndata=136; %数据个数
N=128;%FFT所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,3),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅'); title('Ndata=136 Nfft=128');grid on;
Ndata=136; %数据个数
N=512; %FFT所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,4),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅'); title('Ndata=136 Nfft=512');grid on;
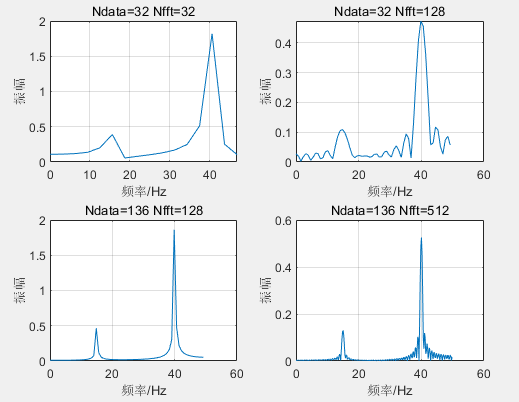
结论:
(1)当数据个数和FFT采用的数据个数均为32时,频率分辨率较低,但没有由于添零而导致的其他频率成分。
(2)由于在时间域内信号加零,致使振幅谱中出现很多其他成分,这是加零造成的。其振幅由于加了多个零而明显减小。
(3)FFT程序将数据截断,这时分辨率较高。
(4)也是在数据的末尾补零,但由于含有信号的数据个数足够多,FFT振幅谱也基本不受影响。
对信号进行频谱分析时,数据样本应有足够的长度,一般FFT程序中所用数据点数与原含有信号数据点数相同,这样的频谱图具有较高的质量,可减小因补零或截断而产生的影响。
信号的时域采样点N和频域采样点数NFFT不同
%如果采样的时间周期是信号周期的倍数,可能泄露就会避免。频谱泄露是由于非整周期采样导致的。错误的观念:信号的时域采样点N必须和FFT的计算点数NFFT相同,才会给处理和解释带来便利。原来是模型的不同产生的影响,采用模拟频率 f 建模不会产生末尾补零使得FFT频率不一致的问题,
例3:x=cos(2*pi*0.24*n)+cos(2*pi*0.26*n)
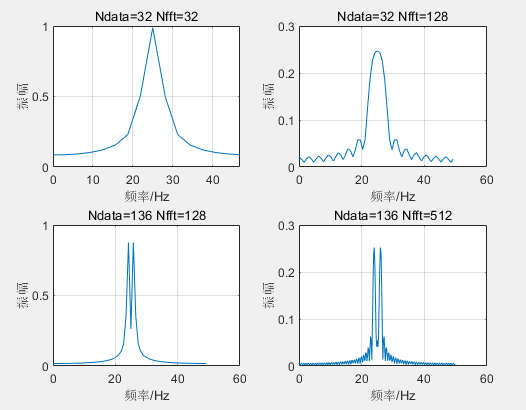
(1)数据点过少,几乎无法看出有关信号频谱的详细信息;
(2)中间的图是将x(n)补90个零,幅度频谱的数据相当密,称为高密度频谱图。但从图中很难看出信号的频谱成分。
(3)信号的有效数据很长,可以清楚地看出信号的频率成分,一个是0.24Hz,一个是0.26Hz,称为高分辨率频谱。
可见,采样数据过少,运用FFT变换不能分辨出其中的频率成分。添加零后可增加频谱中的数据个数,谱的密度增高了,但仍不能分辨其中的频率成分,即谱的分辨率没有提高。只有数据点数足够多时才能分辨其中的频率成分。
1)FFT的算法与奈奎斯特频率没有关系,奈奎斯特频率只是用来避免频率的混叠。
2)对称是因为fft本身算法产生的吧!奈奎斯特频率是系统最高频率*2得到的最低采样频率,和fft没有关系啊,如果低于奈奎斯特频率采样,就会发生频谱混叠,是把大于系统最高频率的部分对称加到小于的部分,发生混叠现象。
3)"频谱图是以Nyquist频率为对称轴的"这句话不对。对称轴是N/2.
上面内容说明了fft纵坐标的问题,下面我总结了坐标问题如下:
1)如果你用fft(NFFT)计算振幅谱,且fft变换后的点数为NFFT的话,那么将得到的振幅谱abs(fft(x))的结果乘以2然后除以N。
1.FFT变换细节问题
1. 信号的时域采样点N和频域采样点数相同
%%%%%%%
clear all; close all;
Adc = 1.25; %直流分量幅度
A1 = 1; %频率F1信号的幅度
A2 = 0.25; %频率F2信号的幅度
F1 = 100; %信号1频率(Hz)
F2 = 1000; %信号2频率(Hz)
Fs = 5120; %采样频率(Hz)
Ts = 1/Fs; %时域采样间隔,采样周期
P1 = -30; %信号1相位(度)
P2 = 90; %信号2相位(度)
N = 256; %采样点数,请注意时域采样N点,FFT时也是N点!
t = [0 : 1/Fs : N/Fs]; %采样时刻,注意不是序列的真正的时间!t = [0:N]*Ts
% t = [0 : N]//Fs; %共采样257个点,为了好看起见多采样了最后一个点,
%最后一个点在实际中应该是下一个采样周期的第一个点
%考虑相位和直流偏置
S1=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);
%显示原始信号
plot(S1);title('原始信号');
figure;
Y = fft(S1,N); %做FFT变换
Ayy = (abs(Y)); %取模
plot(Ayy(1:N)); title('FFT 模值');%显示原始的FFT模值结果
F = ([1:N] - 1) * Fs / N; %换算成实际的频率值,Fs/2 对应着w = pi
Ayy = Ayy / (N / 2); %换算成实际的幅度
Ayy(1) = Ayy(1) / 2;
figure; plot(F(1:N/2), Ayy(1:N/2)); %显示换算后的FFT模值结果,
title('实际幅度-频率曲线图-abs后修正');%只看0~Fs/2正频谱部分
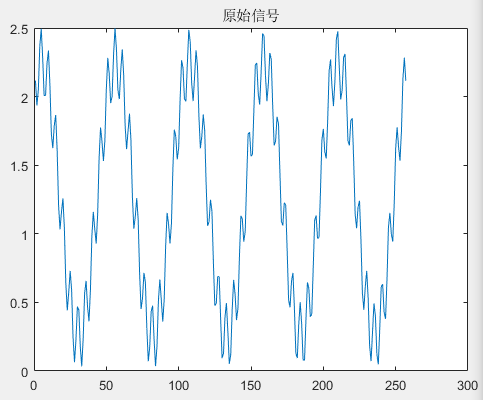
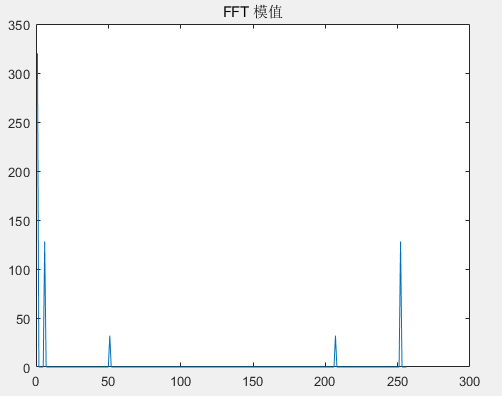
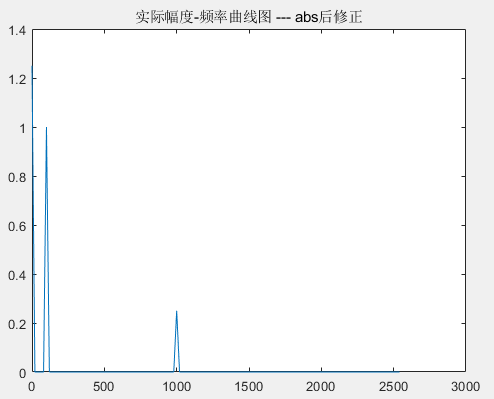
%假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应,该频率下的信号的幅度(对于直流信号是除以N),根据公式验证---某点n所表示的频率为:Fn=(n-1)*Fs/N,因为没有fftshift
f1=(6-1)*5120/256=100 (Hz)---- 验证结果正确,f2=(51-1)*5120/256=1000(Hz)---- 验证结果正确,根据公式验证---对于n=1点的信号,是直流分量,幅度即为A1/N-A1=320/256=1.25,验证结果正确。对于n点(n≠1,且n<=N/2),幅度A=An/(N/2)=128/(256/2)=1---验证结果正确.
看下面的程序。
clear; close all;
% f1 = 20Hz, f2 = 40Hz %若 f1 = 15 可以观察频谱泄露情况
% (1)数据个数Ndata=32,FFT所用的采样点数NFFT=32
fs=240; %采样频率
Ndata=32; %数据长度
N=32; %FFT的数据长度
n=0:Ndata-1;t=n/fs; %数据对应的时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %时间域信号,可以发现频谱泄露
y=fft(x,N); %信号的Fourier变换
mag=abs(y); %求取振幅
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,1),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');title('Ndata=32 Nfft=32');grid on;
%(2)数据个数Ndata=32,FFT所用的采样点数NFFT=128
Ndata=32; %数据个数
N=128; %FFT采用的数据长度
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');title('Ndata=32 Nfft=128');grid on;
%(3)数据个数Ndata = 136,FFT所用的采样点数NFFT=128
Ndata=136; %数据个数
N=128; %FFT采用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,3),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');title('Ndata=136 Nfft=128');grid on;
%(4)数据个数Ndata=136,FFT所用的采样点数NFFT=512
Ndata=136; %数据个数
N=512; %FFT所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,4),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');title('Ndata=136 Nfft=512');grid on;
% (5)数据个数Ndata=136,FFT所用的采样点数NFFT=4096
Ndata=136; %数据个数
N=4096; %FFT所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
figure,plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');title('Ndata=136 Nfft=512');grid on;
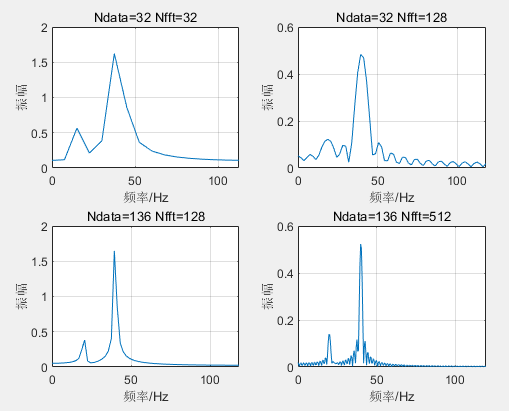
3. 信号的时域采样点N和频域采样点数NFFT不同 -- 比较两种不同的信号模型
clear; close all;
FFT之频率与幅值为何要除以(N/2)
FFT之后得到的一系列复数,是波形对应频率下的幅度特征,注意这个是幅度特征(特征值)不是幅值。
进行FFT变换,获取频率:
FFT傅里叶变换并没对频率进行任何计算,频率只与采样率和进行傅里叶变换的点数相关,注意这里是进行傅里叶变换的点数而不一定是信号的长度。
FFT变换完:
第一个数是0Hz频率,0Hz就是没有波动,叫直流分量。
第二个数,对应的频率是0Hz+Δf频谱分辨率,每隔一个加一次,频谱分辨率Δf计算公式如下:Δf=Fs/N .式中:Fs为采样频率,N为FFT的点数,因此只要Fs和N定了,频域就定下来了。
FFT变换后的第一个实数-直流分量
FFT之后的第一个结果表示了时域信号中的直流成分的多少,所谓直流信号,代表和基准0的偏移量。
上面的结果不好说明,下面再看一个例子:
print(rfft([1,1,1,1,1,1,1,1]))
#输出[8.+0.j 0.-0.j 0.+0.j 0.+0.j 0.+0.j]
明明直流分量为1,但计算结果是8,重点来了,这里又引入一个问题,FFT之后的数值不是真实的幅值,需要进行转换,第一个点需要除以N,才能还原为原来的结果。
FFT变换后的复数模 - 幅度
假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍
这是因为傅里叶级数对应时域幅值,其中已经包含了1/N项,而FFT变换中没有该系数,因此,进行FFT变换后,需除以N/2才能与时域对上。
FFT的计算公式
目录
1、Matlab FFT 函数介绍
2、Matlab FFT 程序
3、FFT 程序分析
3.1 fs 、N 对 FFT 图像幅值的影响。
3.2 直流分量、噪声分量对 FFT 图像的影响
3.3 总结
1、Matlab FFT 函数介绍
FFT (Fast Fourier Transform) 中文为快速傅里叶变换,作用是将离散的时域信号变换到频域,在一般情况下,时域信号都比较难看出特征,但是转换成频域后,就比较容易看出来,因此,很多信号分析都会采用FFT变换,然后对信号进行频谱分析。
Matlab 中,FFT 函数的语法如下:
Y = fft(X)
Y = fft(X,n)
Y = fft(X,n,dim)
推荐直接在命令行使用 help fft看到更加详细的描述信息与例程,这里主要记录一下用法以及注意事项。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方,但是这里直接取读取出来的样本数作为N。
FFT 计算公式如下:
Xk 长度与 N 相同。
根据奈科斯特定律,只有 f=fs/2 范围内的信号才是被采样到的有效信号,因此得到的频谱肯定是关于 N/2 对称的(就是只看前一半的波形就好)。
第k点的实际频率的计算为 f(k) = k * (fs / n) — — (横轴的频率范围为 :f = n * fs / N;)
X[0] 为直流分量 ,幅值 = 模值(X[0]) / N
X[k] 为个点的频率分量(除X[0]外),幅值 = 模值(X[k]) / (N / 2)
2、Matlab FFT 程序
先摆上代码,运行一下看效果。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能:FFT 运用方法(例程) %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 描述
% 使用 Matlab 的 FFT,有一个注意事项,采样数量是采样频率的整数倍,且最好是 2 的 n 次幂。
% 否则会导致采样分辨率匹配不上,表现为在对应的频点处没有采样到,出现偏移,因此会导致
% 描绘图像时,发现所需要的频点处显示出来的幅度值小于预期的值。
% 可以通过修改参数定义的值得定义来直观的看FFT的效果
%% 参数定义
A1 = 2; % 信号1 幅值(A)
f1 = 11; % 信号1 频率(f)
A2 = 0.5; % 信号2 幅值(A)
f2 = 29; % 信号2 频率(f)
A3 = 1; % 信号3 幅值(A)
f3 = 51; % 信号3 频率(f)
Dc = 0; % 直流分量
Noise = 0; % 噪声大小
fs = 128; % 采样频率 (fs)
N = 1024; % 采样点数(样本数量)
%% 运算(生成时域曲线、FFT计算)
n = 0:N-1; % 等差生成序列,
t = n / fs; % 时间序列,用于下式
RA = rand(1,N); % 随机噪声(0~1)
RA = RA - mean(RA); % 减去噪声均值(-0.5~0.5),去除噪声中的直流分量。
x = Dc + A1 * sin(2*pi*f1*t) + A2 * sin(2*pi*f2*t) + A3 * sin(2*pi*f3*t)+ Noise * RA ; % 两个正弦信号、直流分量、噪声相叠加
y = abs(fft(x,N)); % 对上式进行 N 点 FFT 计算 ,并取模值
A = y * 2 / N; % 模值转换为幅值
A(1) = A(1) / 2; % 根据公式 ,X[0] 不用乘以 2
f = n * fs / N; % 转换为频率区间
%% 绘图
subplot(2,1,1);
plot(t,x);
xlabel('时间/s');ylabel('振幅');
title('时域曲线')
subplot(2,1,2);
plot(f(1:N/2),A(1:N/2)); % 描绘图像
xlabel('频率/Hz');ylabel('振幅');
title(['幅频特性曲线 :Fs = ',num2str(fs),', N = ',num2str(N)])
运行图片:
3、FFT 程序分析
通过运行上面的代码,可以得到与上图一致的运行效果,该程序中,原函数是由 直流分量、信号1、信号2、信号3、噪声分量 叠加而成的(上图中暂时将直流分量与噪声分量设置为0),在实际工程使用中,将例程中生成的原函数替换成需要进行分析的序列就可以了。
上面的图片中,每一个信号的幅值就刚好等于所设置的振幅,此处有一个地方需要注意的就是,一般情况下,采样点 N 都不固定,都是随输入的因素影响,例如对一首采样率为 44.1KHz 的歌来分析,读取出来的数据长度 N 就不一定是 2 的n次方了,如果直接送入进行 FFT 计算,到 N 点结算数据,在FFT内由于使用蝶形运算,所以是需要 N 是 2 的 n 次方,因此会导致在 N 个采样点后方补零, 可能在某些频点出看到的赋值,会比预想值要小,这就是能量泄露。如果只需要考虑各频谱值得比例(即只看频率分布情况),不考虑实际 FFT 后的幅值的话,可以直接传入N进去,如果需要进行频谱分析,就要要考虑实际的幅值对分析结果的影响,此处就可以选择加窗,还有一种情况就是 N 足够大,并且是均匀分布,就可以考虑截取 N 的值,使得满足 N 等于 2 的 n 次方.
3.1 fs 、N 对 FFT 图像幅值的影响。
上述程序中,fs = 128;N = 4096;(N 是 fs 的整数倍,且 N 是 2 的 n 次方),下面来分析下不同的 fs 与 N 对实际 FFT 结果的影响。
1、 fs = 100,N = 100(这个情况下,信号 3 不满足 fs ≥ 2f 的情况,因此信号 3 不会显示出来)
2、 增大 N ,fs = 100,N = 150,由于补零了,所以存在能量泄漏,计算出来的幅值会变小。
3、 增大Fs,fs = 200,N=150,此时由于 N 与 fs 仍然是非整数倍关系,且样本数量不足够大,导致分辨率不足,使得不能够将所有的频率都能够对应上,造成频率泄漏,导致幅值变小。
4、 继续加大 N ,直接扩大10倍,fs = 200,N = 1500,可以观察到随着样本数量增加的时候,幅频特性曲线会变窄,与实际的频率越接近,即精度越高。但是由于 fs 与 N 仍然非整数倍关系,因此仍然会有上一点存在的问题。
5、 这一步,减少 N ,但是设置为 fs 的整数倍(往上滑,与第1点对比),fs = 100, N = 200,可以看出,与第 1 点对比的时候,幅值依然是实际值,但是精度更高了(由于N 的数多了一倍)
6、 (对照组)扩大 N 为 fs 的 2 倍(与第 3 、5 点对比)fs = 200,N= 400,因为同样 N 是 fs 的整数倍,幅值为实际值。
7、 最后,设置 fs、N 均为 2 的 n 次方,这里的 fs 根据最高信号频率来选择即可,比如信号 3 是频率最高的信号(51Hz),因此 fs 选择128,N尽量的大,因此 N 选择 4096,此时时域信号中的频率信息,都能够很好的表示出来。
3.2 直流分量、噪声分量对 FFT 图像的影响
在这一节考虑将直流分量,与噪声信号加入,通过改变以下两项来加入。其他值使用默认的参数(fs = 128,N = 1024)
设置直流分量为1,可以看到 FFT 图像 x = 0 处有一个直流分量。(实际使用中,直流分量对信号的分析用处不大,所以一般都会将此值设为0,或者将 用 x = x - mean(x)的方法,将直流分量过滤掉)
按照直流分量的计算公式,需要在程序里对该值进行修改(幅值=模值/N;当x = 0).
修改噪声分量的值 为10,(即叠加一个 幅度为 ±5 的噪声信号),使用噪声前,需要对噪声进行消除直流处理。
可以看出来,在时域的图像上,已经看不清信号的内容了,但是在频域上,仍然能够分辨的出有3个主要信号,并且在采样范围内,均匀分布着噪声信号。后面可以通过设计带通滤波器,将3个有用信号的频段提取出来,其他频段的信号进行过滤,在利用 IFFT 还原出降噪后的波形。
3.3 总结
在能够自己选定 fs 的情况下,尽量选择 fs 为 2 的 n 次方,且 N 取 fs 的倍数,这样可以在幅频特性曲线上,得到与实际相符的幅度值。
fs 固定的情况下,(如音频文件,44.1K/48K/…),不能修改fs,则选择 N 为 fs 的整数倍,通常这种情况下 N 的数量都会足够大,因此 N 向前截取(即N值 ≤ 实际采样点)默认信息是随机分布,最后的一节信号不会对整体的频谱产生较大的影响。(若要考虑全部采样点,则可忽略对实际幅值的影响,实际幅值不一定需要)
叠加噪声的分析,可以转换到频域上进行处理。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号