mysql - 索引深入浅出

 

 

一句话简单来说，索引的出现其实就是为了提高数据查询的效率，就像书的目录一样。一本500页的书，如果你想快速找到其中的某一个知识点，在不借助目录的情况下，那我估计你可得找一

会儿。同样，对于数据库的表而言，索引其实就是它的“目录”。

 

索引的常见模型:

 

1: 哈希表

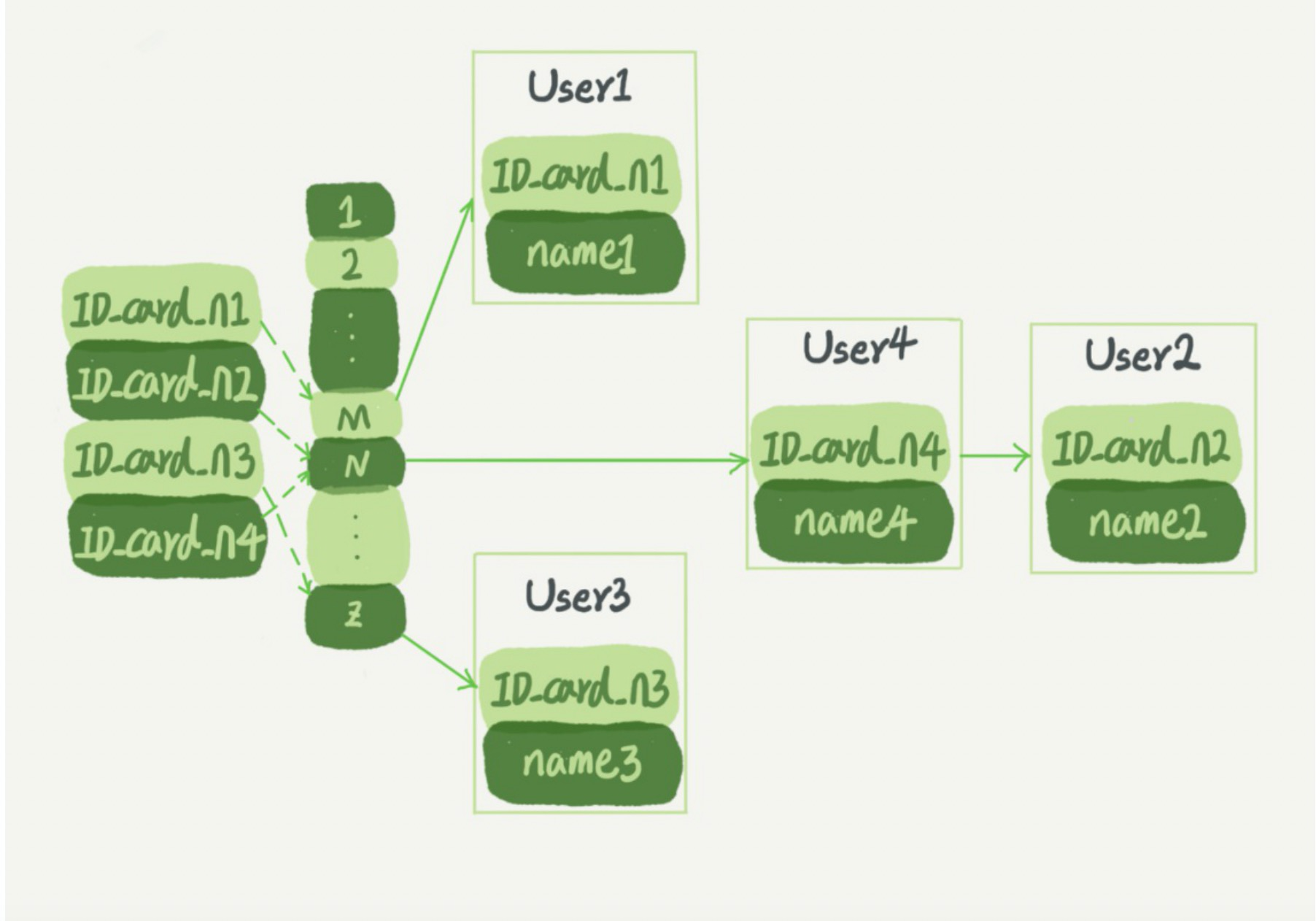
2: 有序数组

3: 搜索树

 

注： 本文主要介绍一下搜索树模型，前两种模型就简单介绍一下

 

数据模型：

 

1: 哈希表

  

哈希表是一种以键-值（key-value）存储数据的结构，我们只要输入待查找的值即key，就可以找到其对应的值即Value。哈希的思路很简单，把值放在数组里，用一个哈希函数把key换算成一个

确定的位置，然后把value放在数组的这个位置。不可避免地，多个key值经过哈希函数的换算，会出现同一个值的情况。处理这种情况的一种方法是，拉出一个链表。

假设，你现在维护着一个身份证信息和姓名的表，需要根据身份证号查找对应的名字，这时对应

的哈希索引的示意图如下所示：

 

图中，User2和User4根据身份证号算出来的值都是N，但没关系，后面还跟了一个链表。假设，这时候你要查ID_card_n2对应的名字是什么，处理步骤就是：首先，将ID_card_n2通过哈希函数算出N；然后，在根据ID_card_n2按顺序遍历，找到User2需要注意的是，图中四个ID_card_n的值并不是递增的，这样做的好处是增加新的User时速度会很快，只需要往后追加。但缺点是，因为不是有序的，所以哈希索引做区间查询的速度是很慢的。你可以设想下，如果你现在要找身份证号在[ID_card_X, ID_card_Y]这个区间的所有用户，就必

须全部扫描一遍了。所以，哈希表这种结构适用于只有等值查询的场景。

 

2: 有序数组

 

顺着上面的思路继续讲解，有序数组在等值查询和范围查询场景中性能是非常优秀的。还是上面这个根据身份证号查名字的例子，如果我们使用有序数组来实现的话，示意图如下所示：

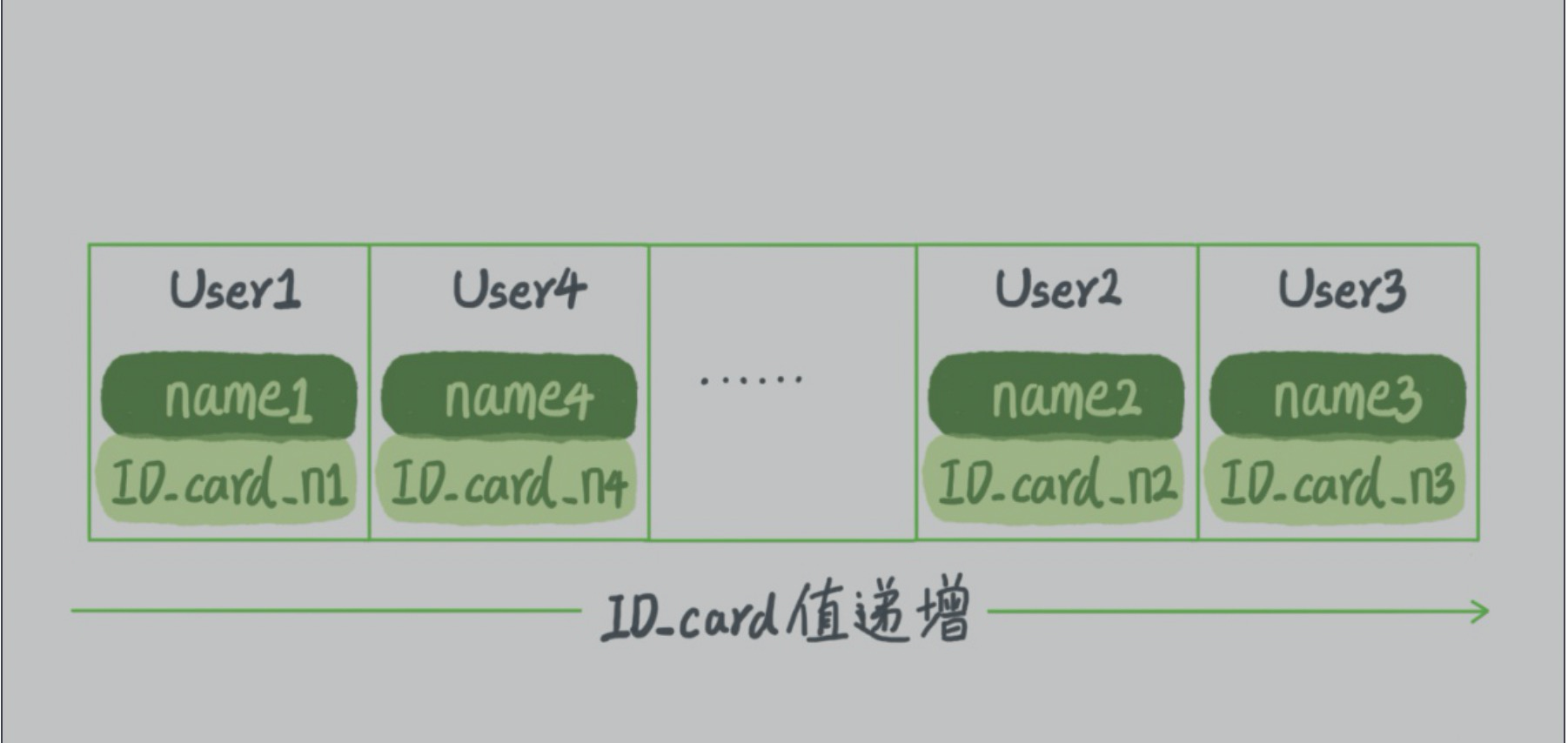
value(id_card_n3)>value(id_card_n2)>...........>value(id_card_n4)>value(id_card_n1)

这里我们假设身份证号没有重复，这个数组就是按照身份证号递增的顺序保存的。这时候如果你要查ID_card_n2对应的名字，用二分法就可以快速得到

 

同时很显然，这个索引结构支持范围查询。你要查身份证号在[ID_card_X, ID_card_Y]区间的User，可以先用二分法找到ID_card_X（如果不存在ID_card_X，就找到大于ID_card_X的第一个User），然后向右遍历，直到查到第一个大于ID_card_Y的身份证号，退出循环。

如果仅仅看查询效率，有序数组就是最好的数据结构了。但是，在需要更新数据的时候就麻烦了，你往中间插入一个记录就必须得挪动后面所有的记录，成本太高。所以，有序数组索引只适用于静态存储引擎

 

 

3: 搜索树

 

3.1 二叉树

二叉搜索树的特点是：每个节点的左儿子小于父节点，父节点又小于右儿子。这样如果你要查ID_card_n2的话，按照图中的搜索顺序就是按照UserA ->UserC->UserF ->User2这个路径得到

 

 

 

树可以有二叉，也可以有多叉。多叉树就是每个节点有多个儿子，儿子之间的大小保证从左到右递增。二叉树是搜索效率最高的，但是实际上大多数的数据库存储却并不使用二叉树。其原因是，索引不止存在内存中，还要写到磁盘上。你可以想象一下一棵100万节点的平衡二叉树，树高20。一次查询可能需要访问20个数据块。在机械硬盘时代，从磁盘随机读一个数据块需要10 ms左右的寻址时间。也就是说，对于一个100万行的表，如果使用二叉树来存储，单独访问一个行可能需要20个10 ms的时间，这个查询可真够慢的。为了让一个查询尽量少地读磁盘，就必须让查询过程访问尽量少的数据块。那么，我们就不应该使用二叉树，而是要使用“N叉”树。这里，“N叉”树中的“N”取决于数据块的大小。

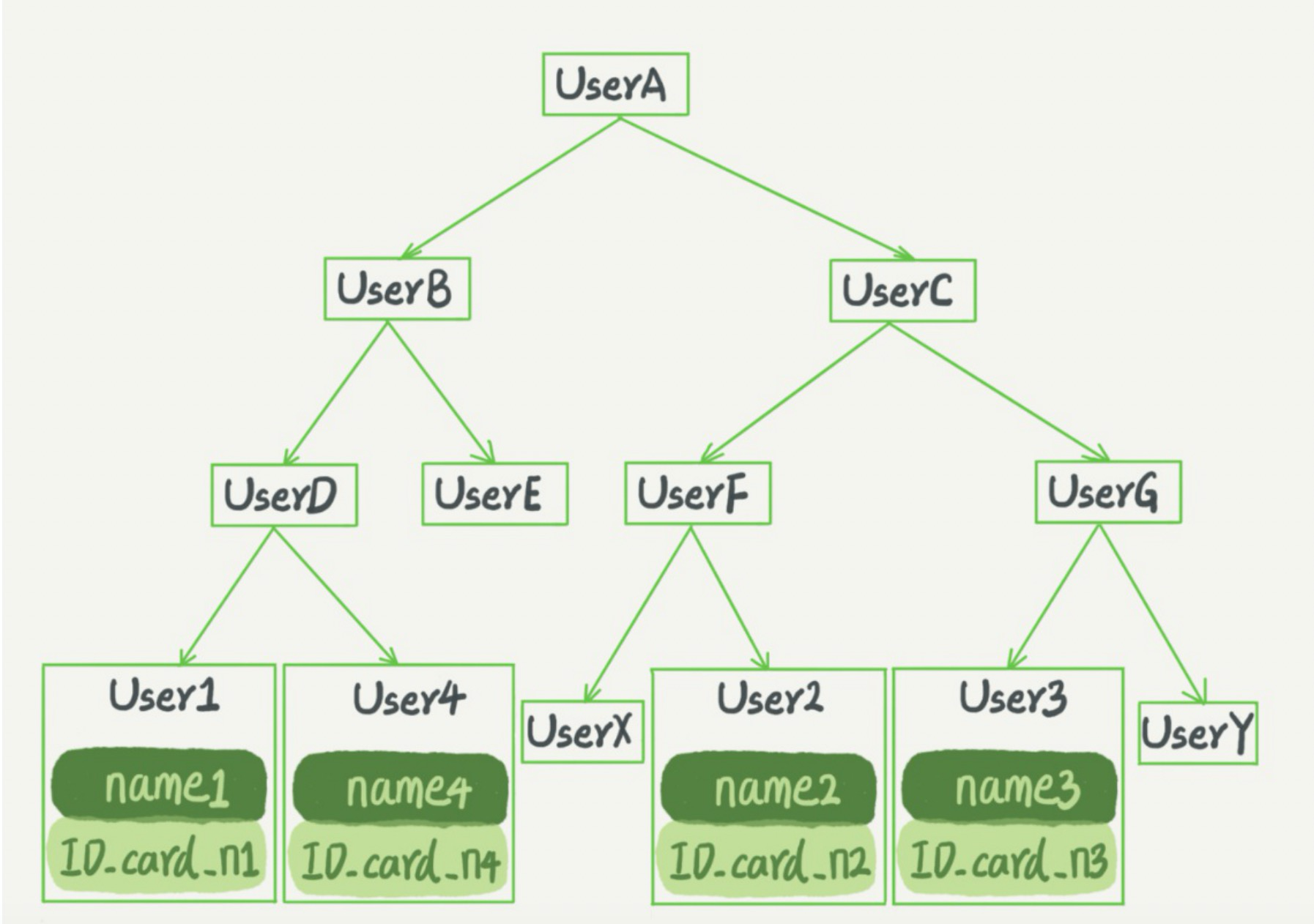
 以InnoDB的一个整数字段索引为例，这个N差不多是1200。这棵树高是4的时候，就可以存1200的3次方个值，这已经17亿了。考虑到树根的数据块总是在内存中的，一个10亿行的表上一个整数字段的索引，查找一个值最多只需要访问3次磁盘。其实，树的第二层也有很大概率在内存中，那么访问磁盘的平均次数就更少了。

 

3.1 N叉树(B+树)

B树分为B-，B，B+树，这里主要讲解B+树，因为Innodb索引用的就是B+树

1: B+树的生成基本步骤

• 1）若为空树，创建一个叶子节点，然后将记录插入其中，此时这个叶子节点也是根节点，插入操作结束。
• 2）针对叶子类型节点：根据key值找到叶子节点，向这个叶子节点插入记录。插入后，若当前节点key的个数小于等于m-1，则插入结束。否则将这个叶子节点分裂成左右两个叶子节点，左叶子节点包含前m/2个记录，右节点包含剩下的记录，将第m/2+1个记录的key进位到父节点中（父节点一定是索引类型节点），进位到父节点的key左孩子指针向左节点,右孩子指针向右节点。将当前节点的指针指向父节点，然后执行第3步。
• 3）针对索引类型节点：若当前节点key的个数小于等于m-1，则插入结束。否则，将这个索引类型节点分裂成两个索引节点，左索引节点包含前(m-1)/2个key，右节点包含m-(m-1)/2个key，将第m/2个key进位到父节点中，进位到父节点的key左孩子指向左节点, 进位到父节点的key右孩子指向右节点。将当前节点的指针指向父节点，然后重复第3步

举例说明: 以5阶B+树为例（5阶B+树节点最多有4个关键字，最少有2个关键字，其中根节点最少可以只有一个关键字），从初始时刻依次插入数据

    1）在空树插入5

     

 

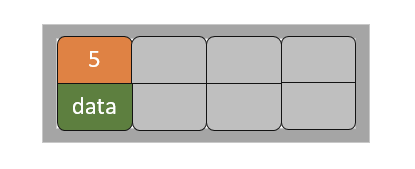
   2）依次插入8,10,15

      

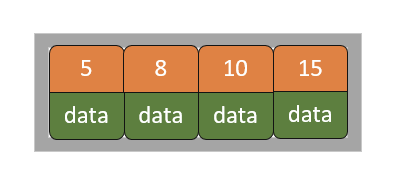
   3）插入16

    

 

 

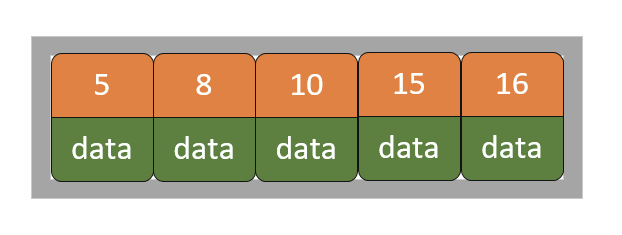
此时节点超过关键字的个数，所以需要进行分裂。由于该节点为叶子节点，所以可以分裂出来左节点2个记录，右边3个记录，中间key成为索引节点中的key（也可以左节点3个记录，右节点2个记录），分裂后当前节点指向了父节点（根节点）。结果如下图所示

 

 

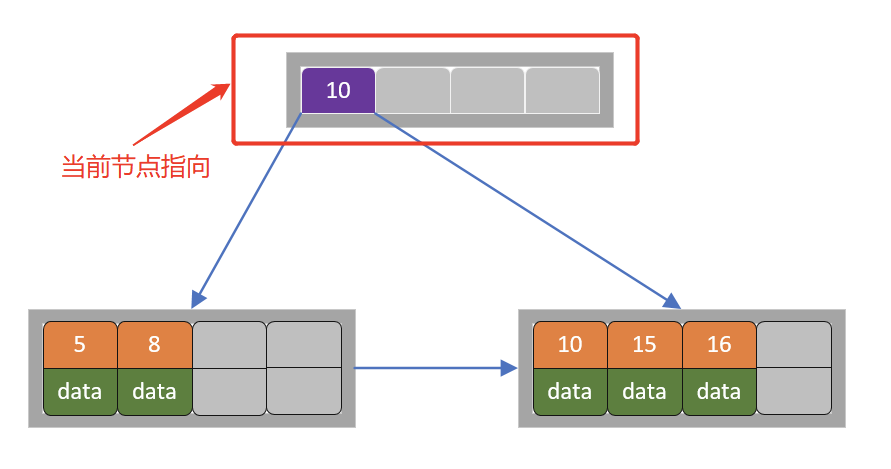
 当前节点的关键字个数满足条件，插入结束

 

4）插入17

 

 

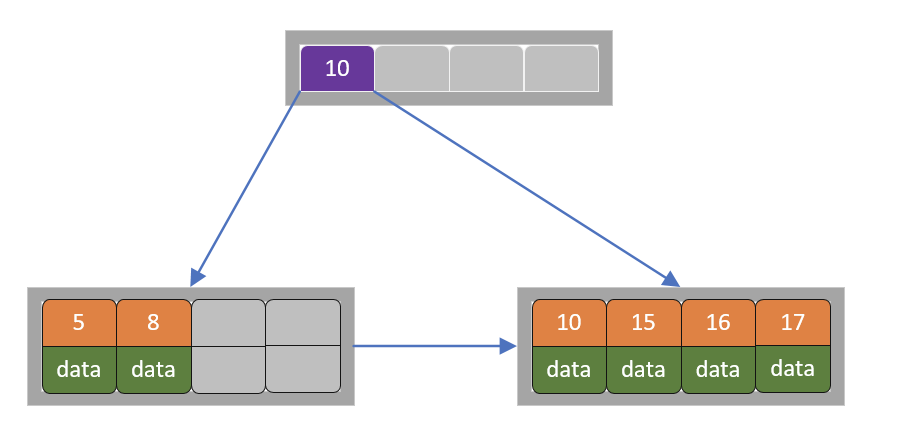
 5）插入18

 

 

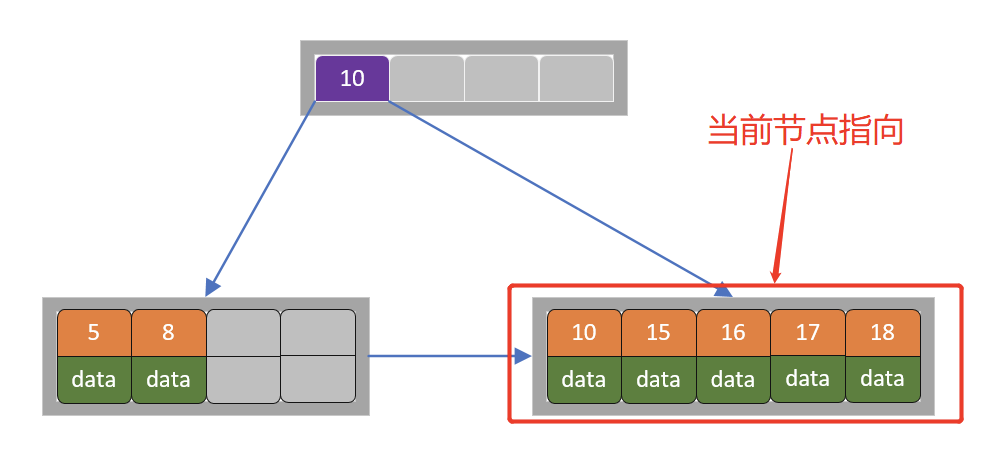
 当前节点超过关键字的个数，进行分裂。由于是叶子节点，分裂成两个节点，左节点2个记录，右节点3个记录，关键字16进位到父节点（索引类型）中，将当前节点的指针指向父节点，如下图所示

 

 

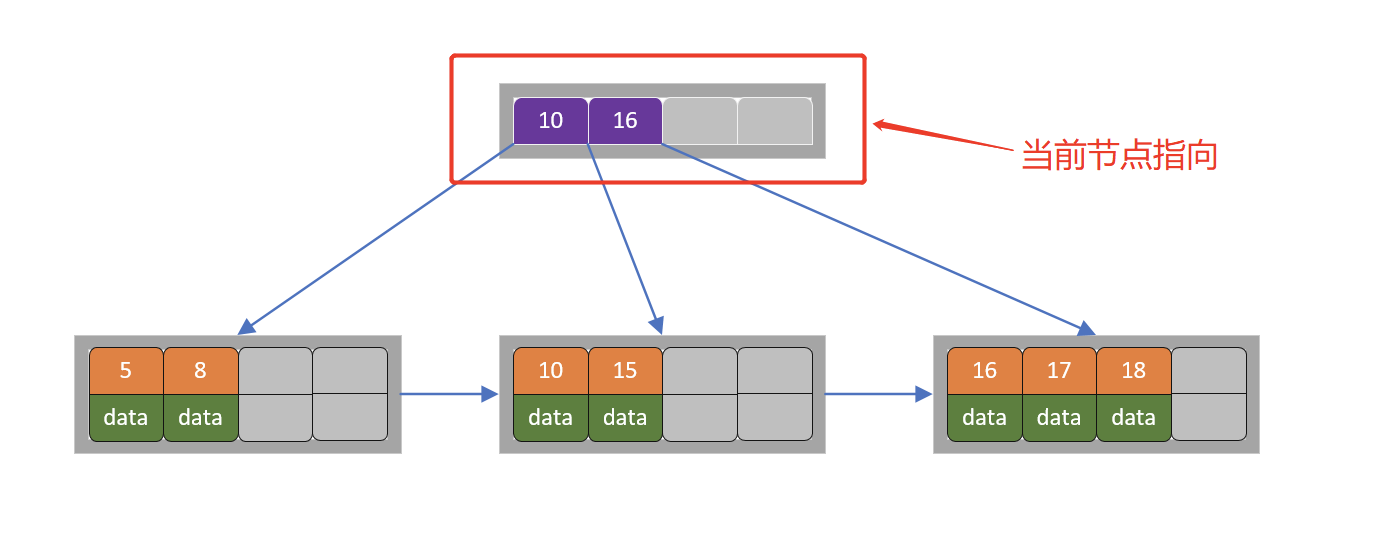
 当前节点的关键字个数满足条件，插入结束

  6）同理继续插入6,9,19，细节不再描述

 

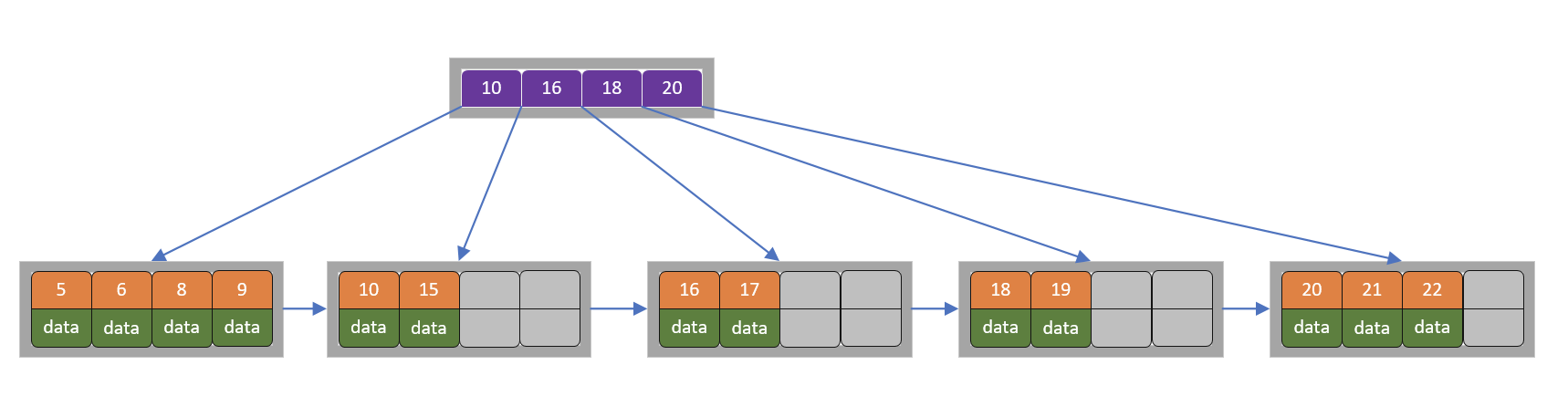
 7）继续插入7

 

 

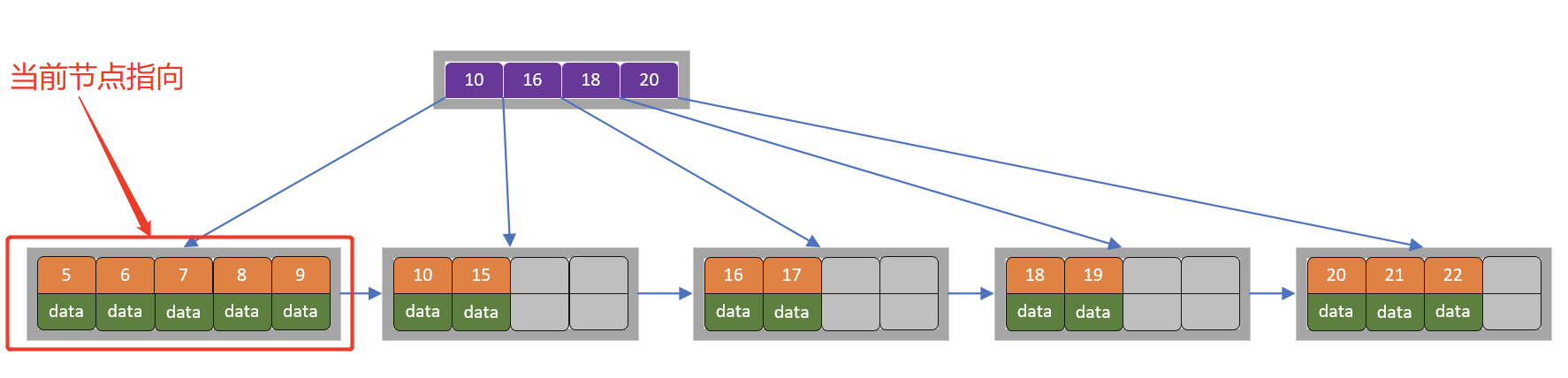
当前节点超过关键字的个数，进行分裂。由于是叶子节点，分裂成两个节点，左节点2个记录，右节点3个记录，关键字7进位到父节点（索引类型）中，将当前节点的指针指向父节点，如下图所示

 

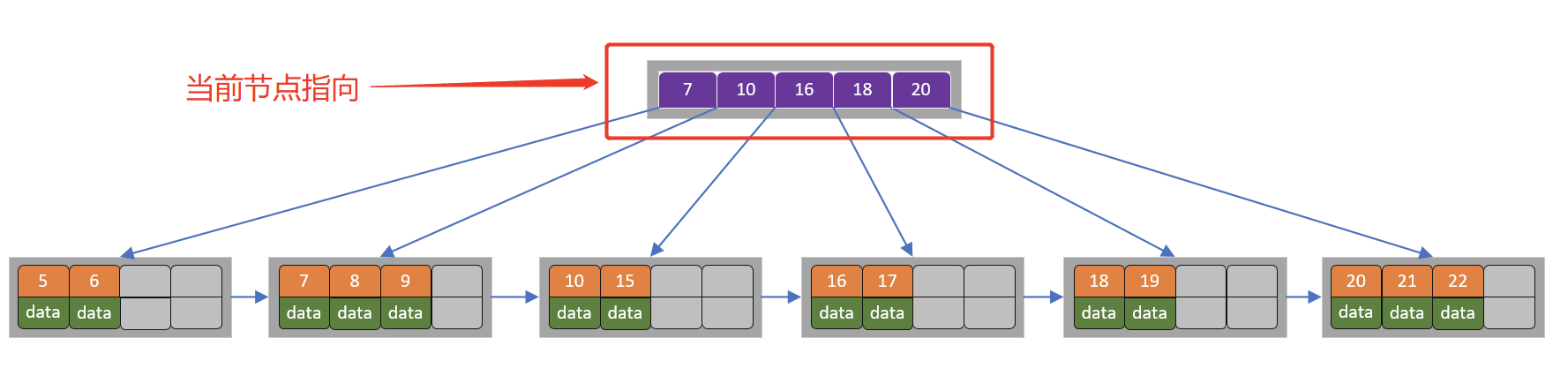
 当前节点超过关键字的个数，进行分裂。由于是索引节点，左节点2个关键字，右节点2个关键字，关键字16进入到父节点中，将当前节点指向父节点，如下图所示

 

 

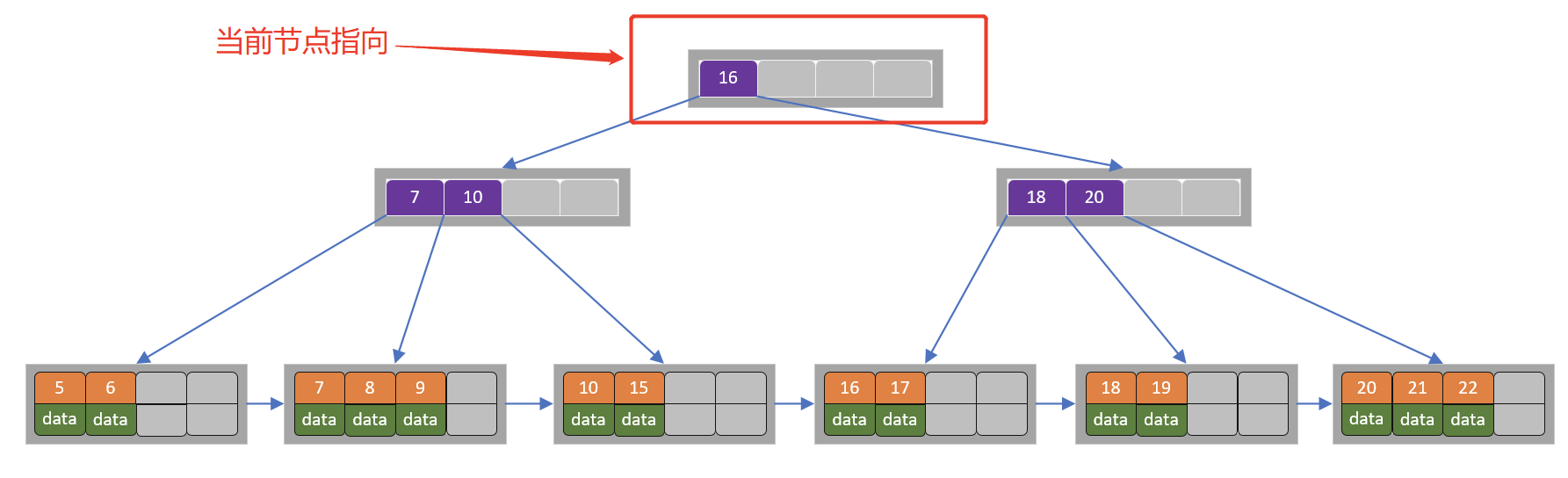
当前节点的关键字个数满足条件，插入结束

2: B+树的删除操作

 

如果叶子节点中没有相应的key，则删除失败。否则执行下面的步骤：

• 1）删除叶子节点中对应的key。删除后若节点的key的个数大于等于Math.ceil(m/2) – 1，删除操作结束,否则执行第2步。
• 2）若兄弟节点key有富余（大于Math.ceil(m/2) – 1），向兄弟节点借一个记录，同时用借到的key替换父结（指当前节点和兄弟节点共同的父节点）点中的key，删除结束。否则执行第3步。
• 3）若兄弟节点中没有富余的key,则当前节点和兄弟节点合并成一个新的叶子节点，并删除父节点中的key（父节点中的这个key两边的孩子指针就变成了一个指针，正好指向这个新的叶子节点），将当前节点指向父节点（必为索引节点），执行第4步
• 4）若索引节点的key的个数大于等于Math.ceil(m/2) – 1，则删除操作结束。否则执行第5步
• 5）若兄弟节点有富余，父节点key下移，兄弟节点key上移，删除结束。否则执行第6步
• 6）当前节点和兄弟节点及父节点下移key合并成一个新的节点。将当前节点指向父节点，重复第4步。

  1）初始状态

 

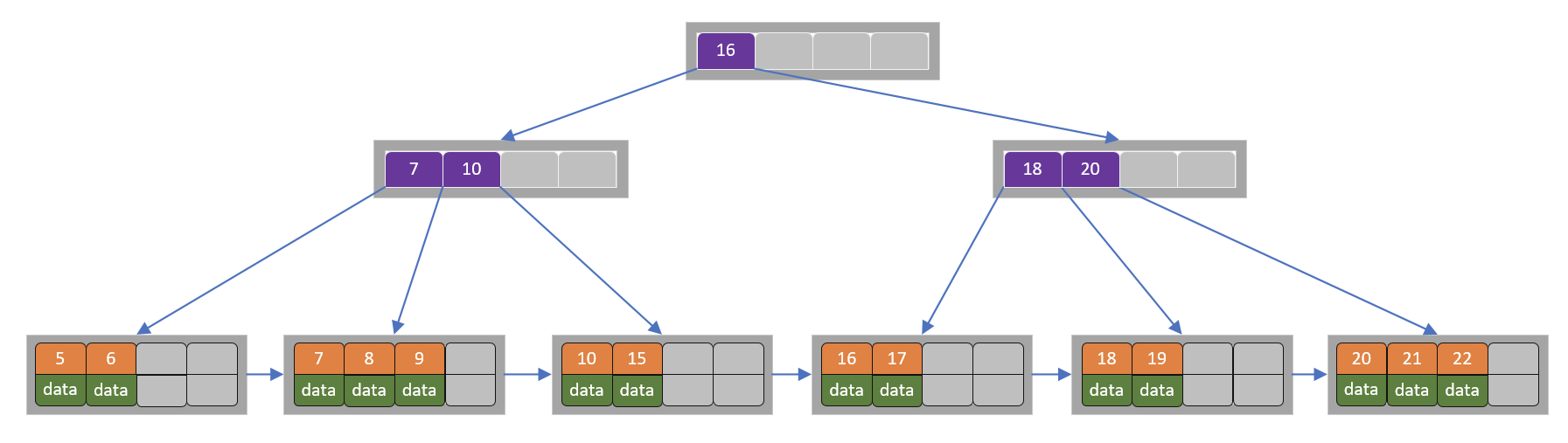
 2）删除22

 

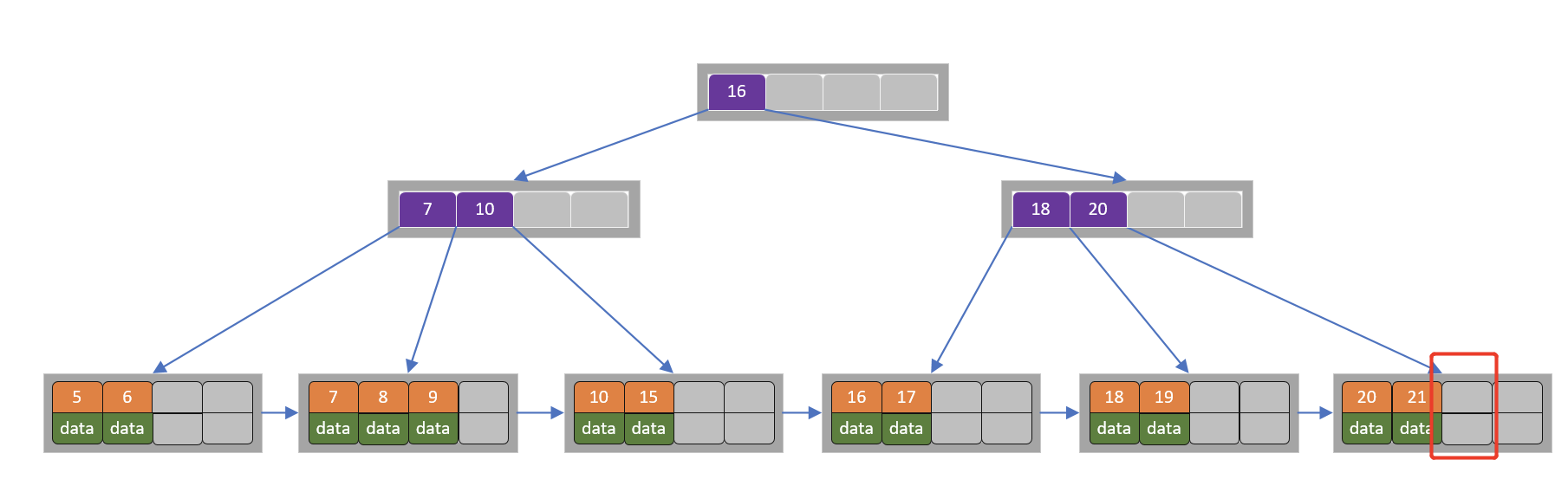
删除后叶子节点中key的个数大于等于2，删除结束

  3）删除15

 

 

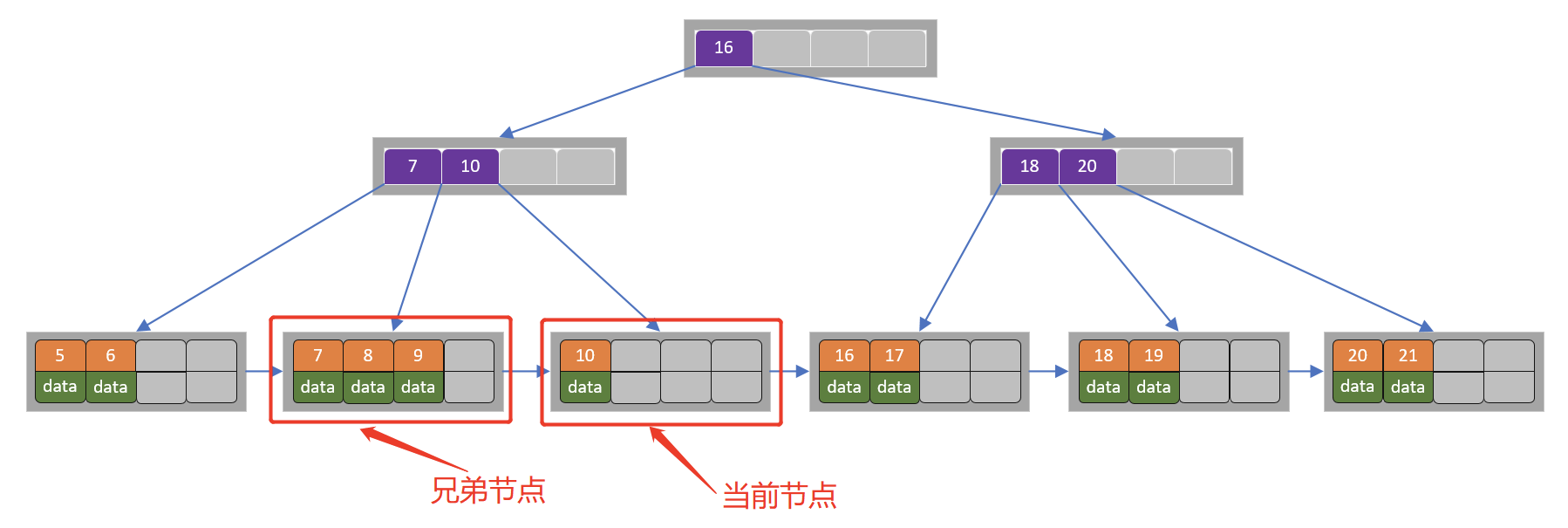
当前节点只有一个key，不满足条件，而兄弟节点有三个key，可以从兄弟节点借一个关键字为9的记录,同时更新将父节点中的关键字由10也变为9，删除结束。

 

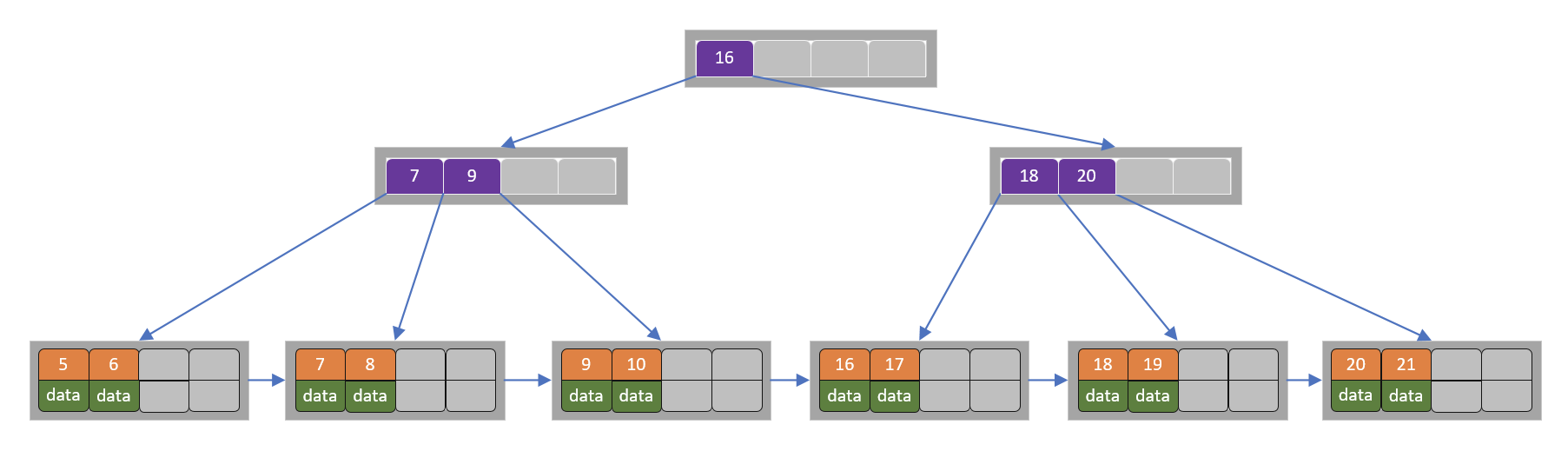
 4）删除7

 

 

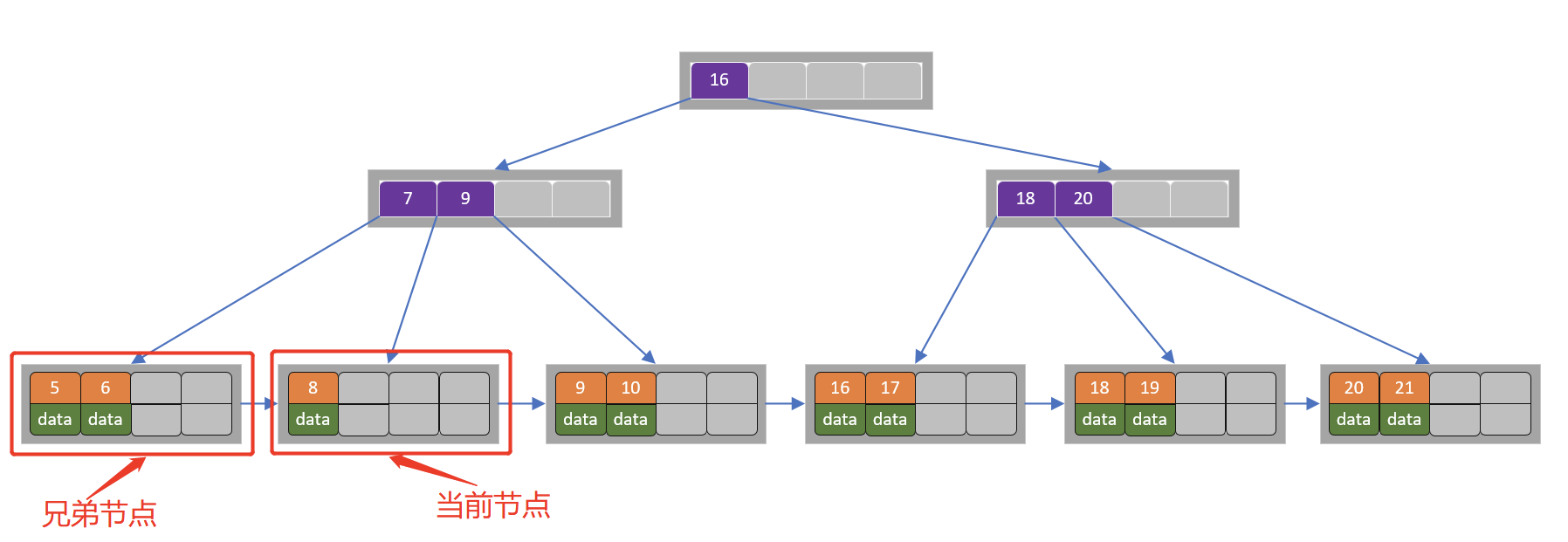
当前节点关键字个数小于2，（左）兄弟节点中的也没有富余的关键字（当前节点还有个右兄弟，不过选择任意一个进行分析就可以了，这里我们选择了左边的），所以当前节点和兄弟节点合并，并删除父节点中的key，当前节点指向父节点。

 

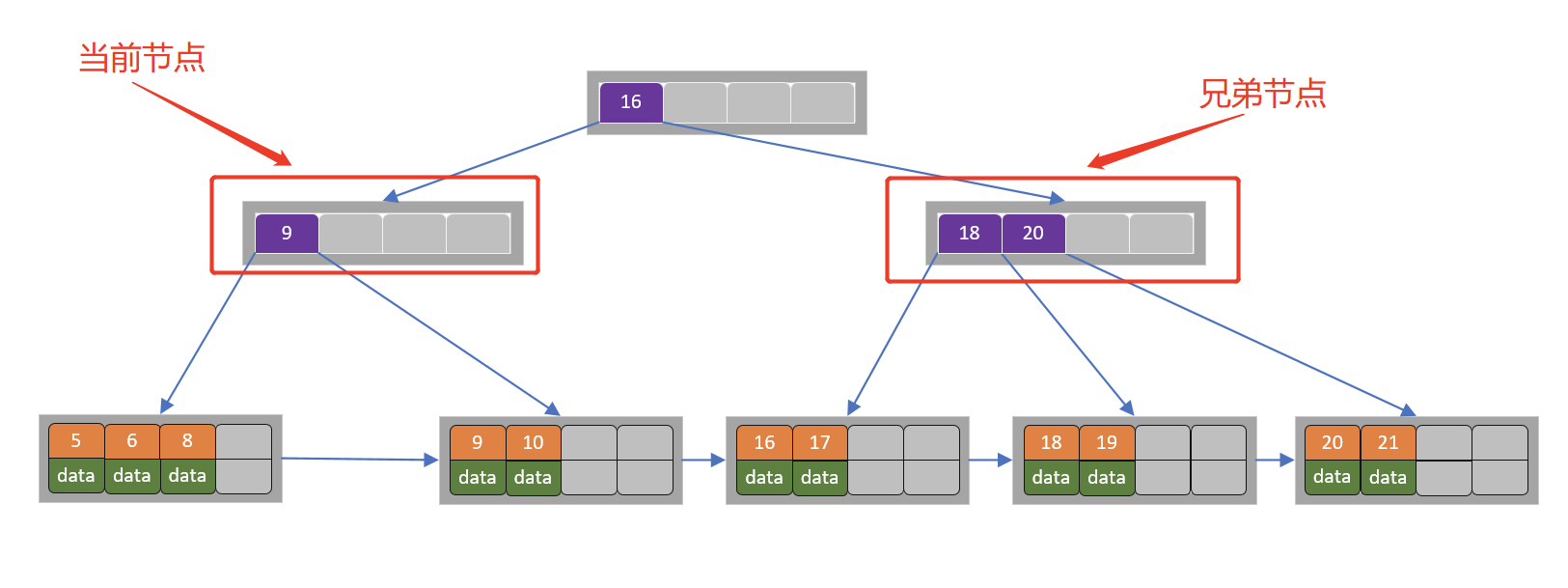
 此时当前节点的关键字个数小于2，兄弟节点的关键字也没有富余，所以父节点中的关键字下移，和两个孩子节点合并，结果如下图所示。

 

 

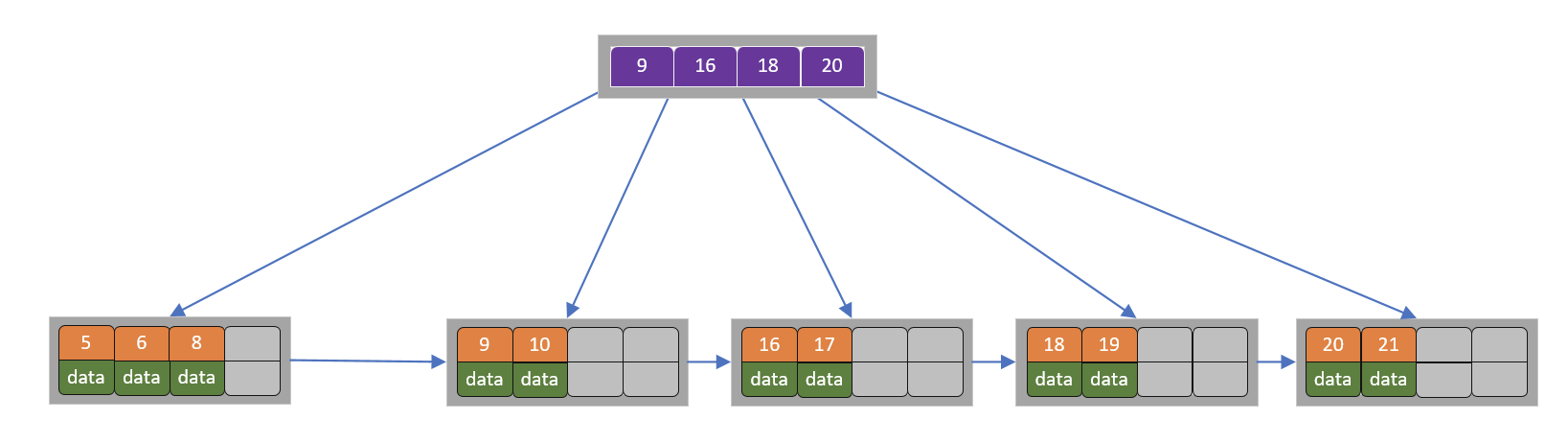
以上，我们将B+树基本讲解完成了，那么我们一起进入相对偏实战的内容吧

在MySQL中，索引是在存储引擎层实现的，所以并没有统一的索引标准，即不同存储引擎的索引的工作方式并不一样。而即使多个存储引擎支持同一种类型的索引，其底层的实现也可能不同。由于InnoDB存储引擎在MySQL数据库中使用最为广泛，所以下面我就以InnoDB为例，和你分析一下其中的索引模型

 

索引：

InnoDB 的索引模型

在InnoDB中，表都是根据主键顺序以索引的形式存放的，这种存储方式的表称为索引组织表。又因为前面我们提到的，InnoDB使用了B+树索引模型，所以数据都是存储在B+树中的。每一个索引在InnoDB里面对应一棵B+树。假设，我们有一个主键列为ID的表，表中有字段k，并且在k上有索引。这个表的建表语句是：

 

mysql> create table T(

id int primary key,

k int not null,

name varchar(16),

index (k))engine=InnoDB;

 

表中R1~R5的(ID,k)值分别为(100,1)、(200,2)、(300,3)、(500,5)和(600,6)，两棵树的示例示意图如下

 

 

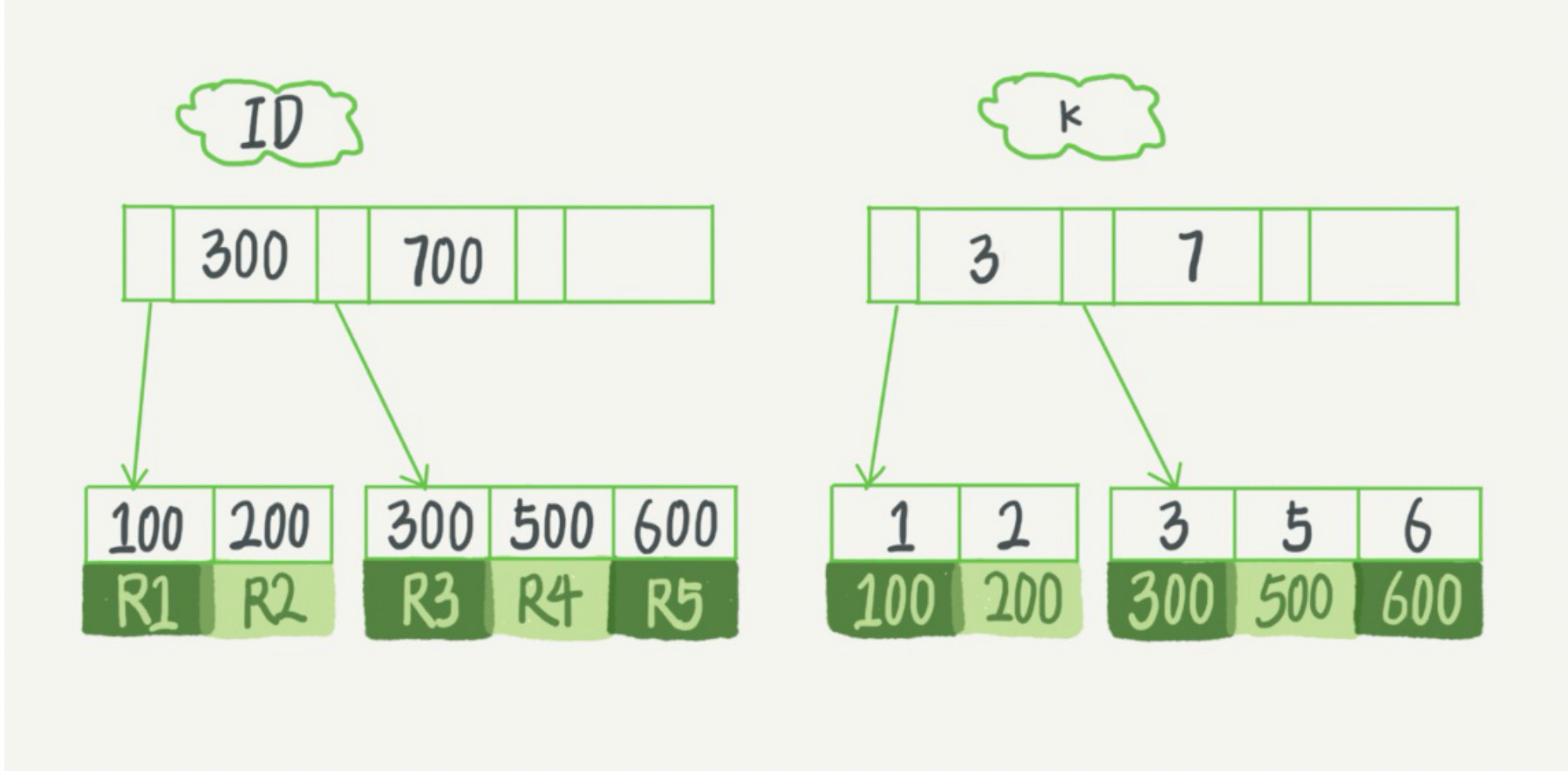
 从图中不难看出，根据叶子节点的内容，索引类型分为主键索引和非主键索引。主键索引的叶子节点存的是整行数据。在InnoDB里，主键索引也被称为聚簇索引（clusteredindex）非主键索引的叶子节点内容是主键的值。在InnoDB里，非主键索引也被称为二级索引

（secondary index）。根据上面的索引结构说明，我们来讨论一个问题：基于主键索引和普通索引的查询有什么区别？

 

如果语句是select *fromTwhere ID=500，即主键查询方式，则只需要搜索ID这棵B+树；

如果语句是select *fromTwhere k=5，即普通索引查询方式，则需要先搜索k索引树，得到ID的值为500，再到ID索引树搜索一次。这个过程称为回表。也就是说，基于非主键索引的查询需要多扫描一棵索引树。因此，我们在应用中应该尽量使用主键查询

索引维护

B+树为了维护索引有序性，在插入新值的时候需要做必要的维护。以上面这个图为例，如果插入新的行ID值为700，则只需要在R5的记录后面插入一个新记录。如果新插入的ID值为400，就相对麻烦了，需要逻辑上挪动后面的数据，空出位置。而更糟的情况是，如果R5所在的数据页已经满了，根据B+树的算法，这时候需要申请一个新的数据页，然后挪动部分数据过去。这个过程称为页分裂。在这种情况下，性能自然会受影响。除了性能外，页分裂操作还影响数据页的利用率。原本放在一个页的数据，现在分到两个页中，

整体空间利用率降低大约50%。当然有分裂就有合并。当相邻两个页由于删除了数据，利用率很低之后，会将数据页做合并。合并的过程，可以认为是分裂过程的逆过程。 

 

 

联合索引

首先，

我们先来看一下这个问题：在下面这个表T中，如果我执行 select *fromTwhere k between 3 and 5，需要执行几次树的搜索操作，会扫描多少行？下面是这个表的初始化语句

mysql> create table T (

ID int primary key,

k int NOT NULL DEFAULT 0,

s varchar(16) NOT NULL DEFAULT '',

index k(k))

engine=InnoDB;

insert into T values(100,1, 'aa'),(200,2,'bb'),(300,3,'cc'),(500,5,'ee'),(600,6,'ff'),(700,7,‘gg’)

 

 

 

现在，我们一起来看看这条SQL查询语句的执行流程：

1. 在k索引树上找到k=3的记录，取得 ID = 300；

2. 再到ID索引树查到ID=300对应的R3；

3. 在k索引树取下一个值k=5，取得ID=500；

4. 再回到ID索引树查到ID=500对应的R4；

5. 在k索引树取下一个值k=6，不满足条件，循环结束。

在这个过程中，回回到到主主键键索索引引树树搜搜索索的的过过程程，，我我们们称称为为回回表表。可以看到，这个查询过程读了k索引树的3条记录（步骤1、3和5），回表了两次（步骤2和4

在这个例子中，由于查询结果所需要的数据只在主键索引上有，所以不得不回表。那么，有没有可能经过索引优化，避免回表过程呢？ 

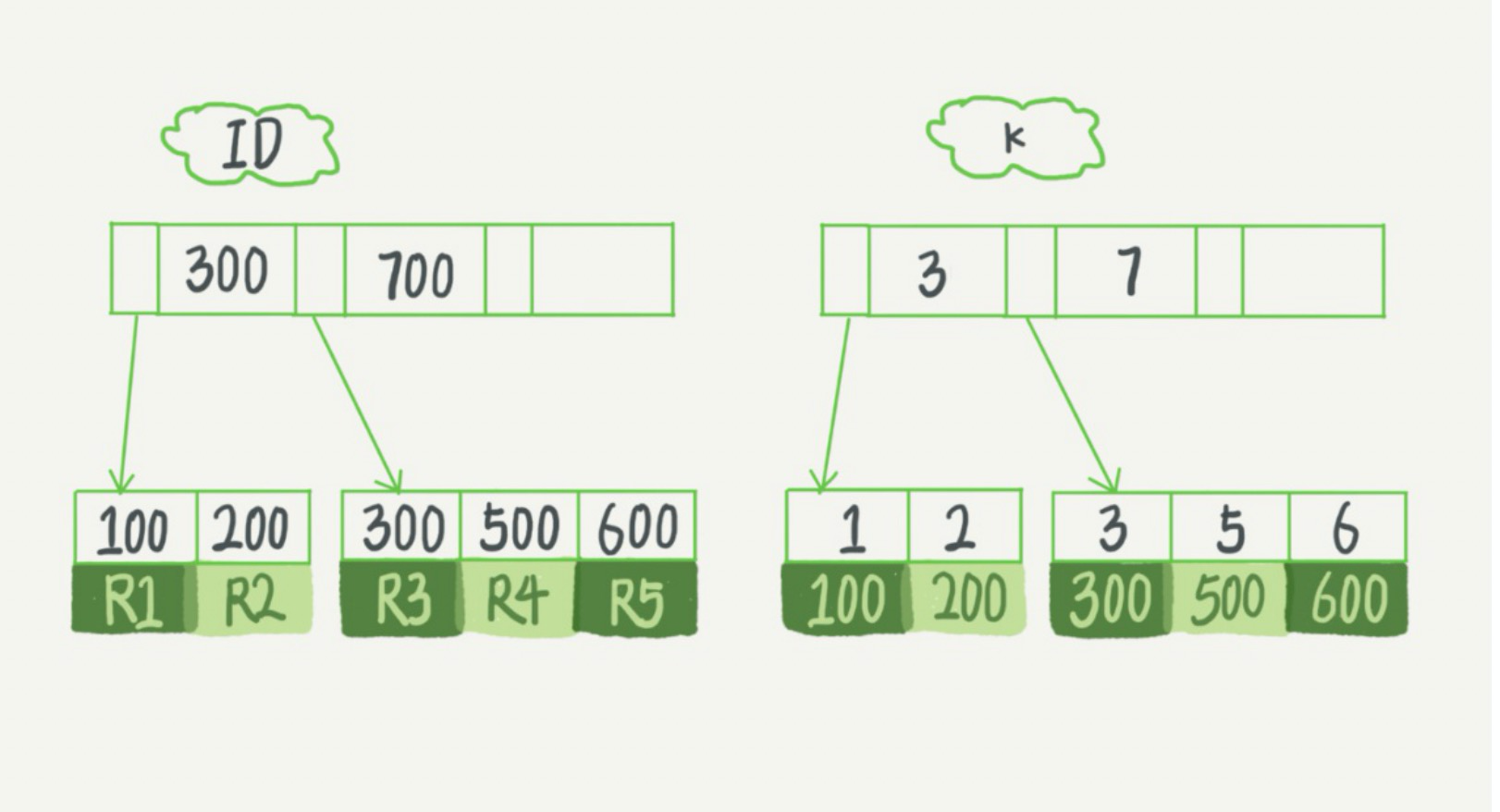
如果执行的语句是select ID fromTwhere k between 3 and 5，这时只需要查ID的值，而ID的值已经在k索引树上了，因此可以直接提供查询结果，不需要回表。也就是说，在这个查询里面，索引k已经“覆盖了”我们的查询需求，我们称为覆盖索引。

 

基于上面覆盖索引的说明，我们来讨论一个问题：在一个市民信息表上，是否有必要将身份证号和名字建立联合索引？

假设这个市民表的定义是这样的：

CREATE TABLE `tuser` (

`id` int(11) NOT NULL,

`id_card` varchar(32) DEFAULT NULL,

`name` varchar(32) DEFAULT NULL,

`age` int(11) DEFAULT NULL,

`ismale` tinyint(1) DEFAULT NULL,

PRIMARY KEY (`id`),

KEY `id_card` (`id_card`),

KEY `name_age` (`name`,`age`)

) ENGINE=InnoDB

 

我们知道，身份证号是市民的唯一标识。也就是说，如果有根据身份证号查询市民信息的需求，我们只要在身份证号字段上建立索引就够了。而再建立一个（身份证号、姓名）的联合索引，是不是浪费空间？

如果现在有一个高频请求，要根据市民的身份证号查询他的姓名，这个联合索引就有意义了。它可以在这个高频请求上用到覆盖索引，不再需要回表查整行记录，减少语句的执行时间。当然，索引字段的维护总是有代价的。因此，在建立冗余索引来支持覆盖索引时就需要权衡考虑了

 

最左前缀原则：

看到这里你一定有一个疑问，如果为每一种查询都设计一个索引，索引是不是太多了。如果我现在要按照市民的身份证号去查他的家庭地址呢？虽然这个查询需求在业务中出现的概率不高，但总不能让它走全表扫描吧？反过来说，单独为一个不频繁的请求创建一个（身份证号，地址）的索引又感觉有点浪费。应该怎么做呢？这里，B+树这种索引结构，可以利用索引的最左前缀来定位记录，为了直观地说明这个概念，我们用（name，age）这个联合索引来分析

 

 

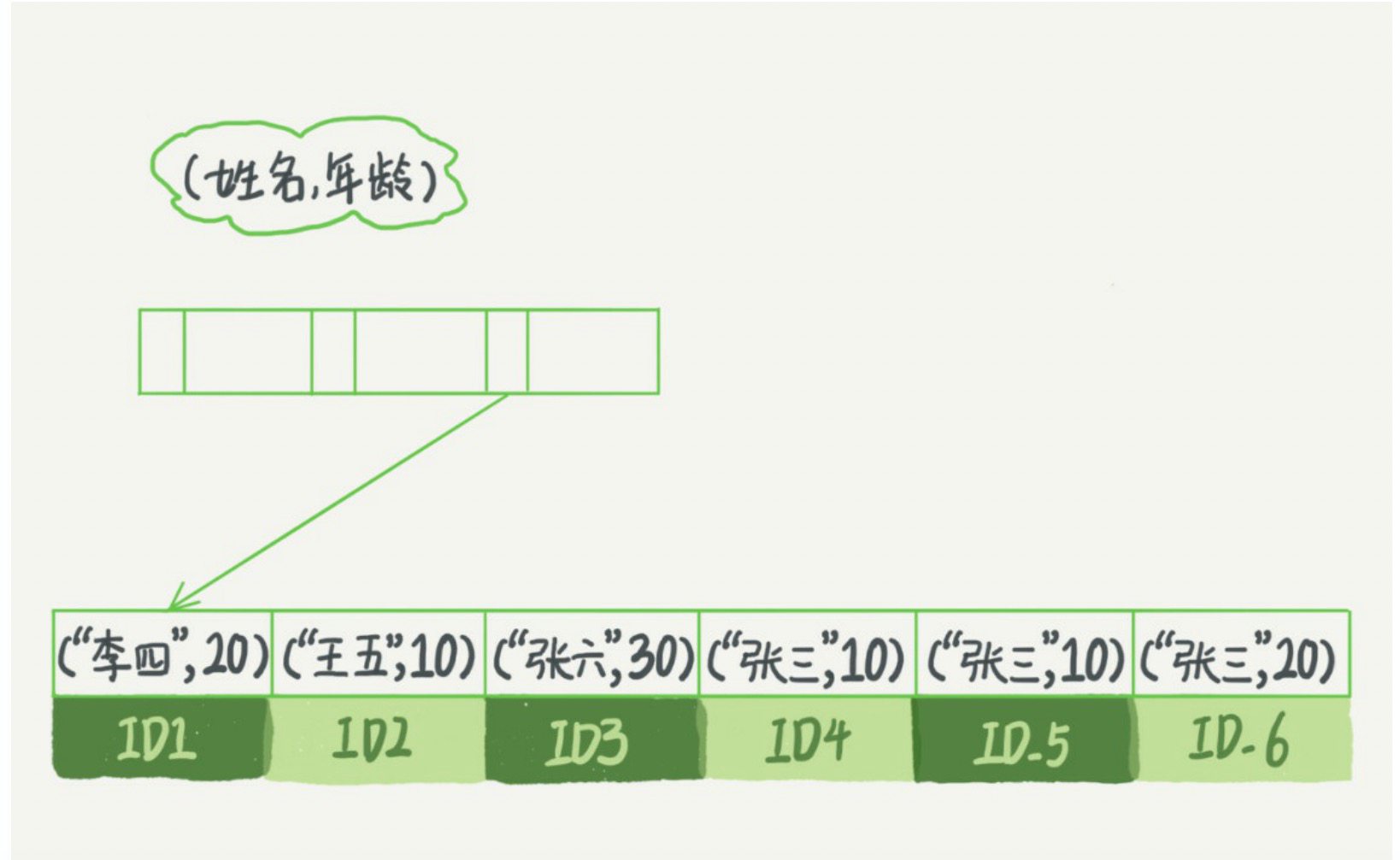
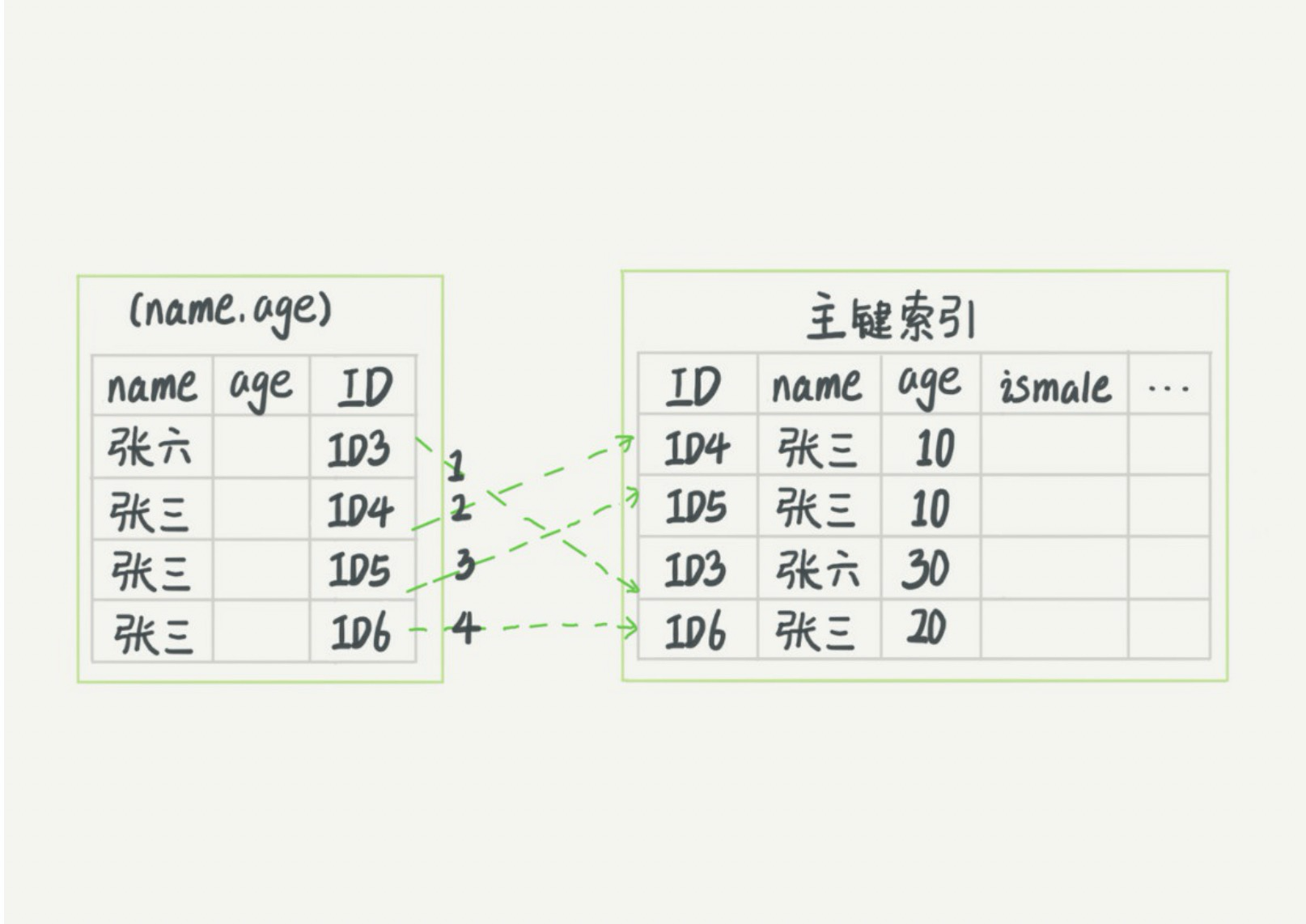
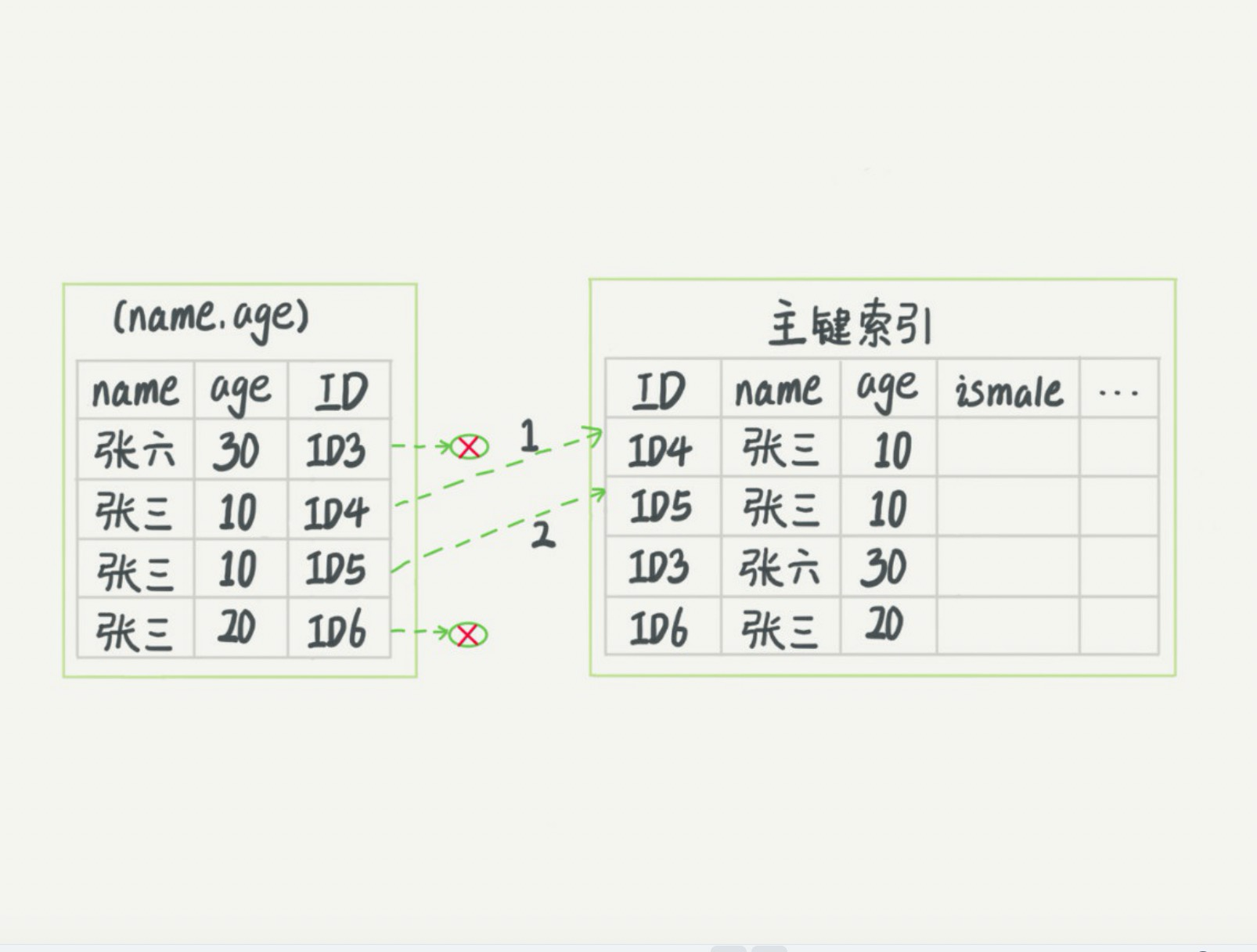
顺序问题: 联合索引存在一个顺序问题，那就是首先以最左的索引对应的值进行排序，在第一个索引相同值的情况下，在对第二个索引排序，一次往下。。 举例：上图中name属于第一索引，所以第一索引是按照name排序的，在name相同的情况下(比如张三),在对第二个索引对应的值进行排序，就如上图的三个张三下age是按照10，10，20排序的.

 可以看到，索引项是按照索引定义里面出现的字段顺序排序的。当你的逻辑需求是查到所有名字是“张三”的人,，可以快速定位到ID4，然后向后遍历得到所有需要的结果。如果你要查的是所有名字名为占山并且年龄为10的人，这时，你也能够用上这个索引，查找到第一个符合条件的记录是ID4，然后向后遍历，直到不满足条件为止,这样可以筛选出ID-4道ID-6的值，然后在遍历第二个条件，ID4满足条件，一次向后便利，直到便利道ID-6大于10，遍历结束(并不是因为ID-6在图中是最后一个值才不继续便利的，因为在第一个索引对应的值相等的情况，第二个索引的值是按照顺序排列的，因为ID-6中age已经>10了，如果后面还存在值肯定也是>=20的，那么肯定满足！=10的条件，所以就没必要向后遍历了)

基于上面对最左前缀索引的说明，我们来讨论一个问题：在建立联合索引的时候，如何安排索引内的字段顺序。。这里我们的评估标准是，索引的复用能力。因为可以支持最左前缀，所以当已经有了(a,b)这个联合索引后，一般就不需要单独在a上建立索引了。因此，第一原原则是，，如果通过调整顺序，可以少维护一个索引，那么这个顺序往往就是需要优先考虑采用的,所以现在你知道了，这段开头的问题里，我们要为高频请求创建(身份证号，姓名）这个联合索引，并用这个索引支持“根据身份证号查询地址”的需求。那么，如果既有联合查询，又有基于a、b各自的查询呢？查询条件里面只有b的语句，是无法使用(a,b)这个联合索引的，这时候你不得不维护另外一个索引，也就是说你需要同时维护(a,b)、(b) 这两个索引

 

索引下推:

上一段我们说到满足最左前缀原则的时候，最左前缀可以用于在索引中定位记录。这时，你可能要问，那些不符合最左前缀的部分，会怎么样呢？我们还是以市民表的联合索引（name, age）为例。如果现在有一个需求：检索出表中“名字第一个字是张，而且年龄是10岁的所有男孩”。那么，SQL语句是这么写的：

 

mysql> select * from tuser where name like '张%' and age=10 and ismale=1;

 

你已经知道了前缀索引规则，所以这个语句在搜索索引树的时候，只能用 “张”，找到第一个满足条件的记录ID3。当然，这还不错，总比全表扫描要好。然后呢？当然是判断其他条件是否满足。

 

在MySQL 5.6之前，只能从ID3开始一个个回表。到主键索引上找出数据行，再对比字段值

 

 

 

 

而MySQL 5.6 引入的索引下推优化（index condition pushdown)， 可以在索引遍历过程中，对索引中包含的字段先做判断，直接过滤掉不满足条件的记录，减少回表次数。图3和图4，是这两个过程的执行流程图。

 

 

 

 

在图3和4这两个图里面，每一个虚线箭头表示回表一次。图3中，在(name,age)索引里面我特意去掉了age的值，这个过程InnoDB并不会去看age的值，只是按顺序把“name第一个字是’张’”的记录一条条取出来回表。因此，需要回表4次。图4跟图3的区别是，InnoDB在(name,age)索引内部就判断了age是否等于10，对于不等于10的记录，直接判断并跳过。在我们的这个例子中，只需要对ID4、ID5这两条记录回表取数据判断，就只需要回表2次。 

 

联合索引的B+树

首先我们来看一个问题，我们有一个表user，有几个字段id、c1、c2、c3、c4，其中id是主键，c1、c2、c3字段建立联合索引，那么执行下面几个SQL，来看一下索引执行情况：

select * from user where c1= 12 and c2= 14 and c3 = 3 // 索引全匹配
select * from user where c1= 12 and c2= 14 // 索引部分匹配
select * from user where c1= 12 and c3 = 3 // 索引部分匹配
select * from user where c2= 12 and c3 = 3 // 索引无法匹配

可以看到，对于联合索引，全部命中索引字段可以执行索引；部分命中并符合最左匹配原则，也可能会执行索引；不满足最左匹配原则，则无法命中索引，那么这是为什么呢？

我们来分析一下对于联合索引的B+树的数据结构

 

 

 

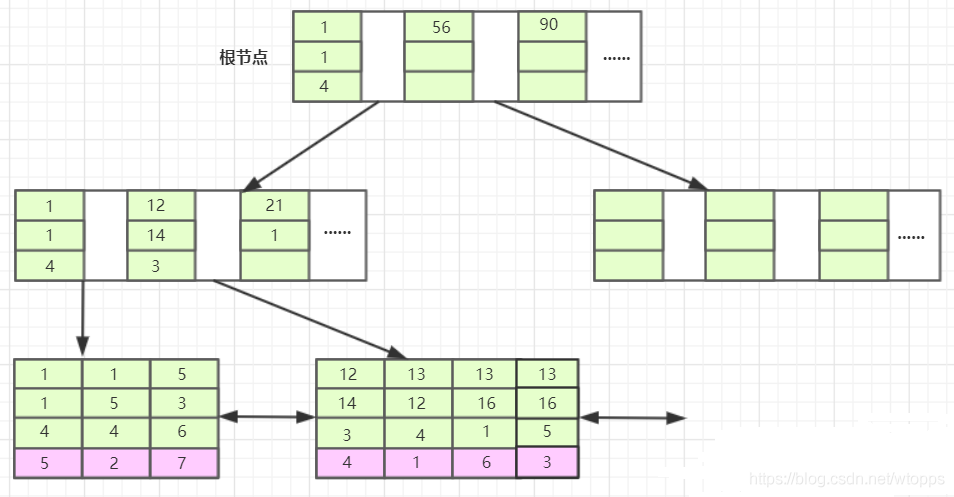
上图就是一个联合索引的B+树示意图，InnoDB会使用聚簇索引在B+树维护索引和数据文件，然后我们创建了一个联合索引name、age、point也会生成一个索引树，同样是B+树的结构，只不过它的data部分存储的是联合索引所在行的主键值。

 

对于联合索引来说只不过比单值索引多了几列，而这些索引列全都出现在索引树上。对于联合索引，存储引擎会首先根据第一个索引列排序，如上图我们可以单看第一个索引列，横着看，如，1 1 5 12 13…他是单调递增的；如果第一列相等则再根据第二列排序，依次类推就构成了上图的索引树，上图中的c1列都等于1时，则根据c2排序，此时c2列也相等则按c3列排序，如：1 1 4 ，1 1 5，c=4在c=5前面，以及13 12 4,13 16 1,13 16 5就可以说明这种情况。

 

联合索引的查找方式

当我们的SQL可以应用到联合索引的时候，比如select * from user where c1= 12 and c2= 14 and c3 = 3 。

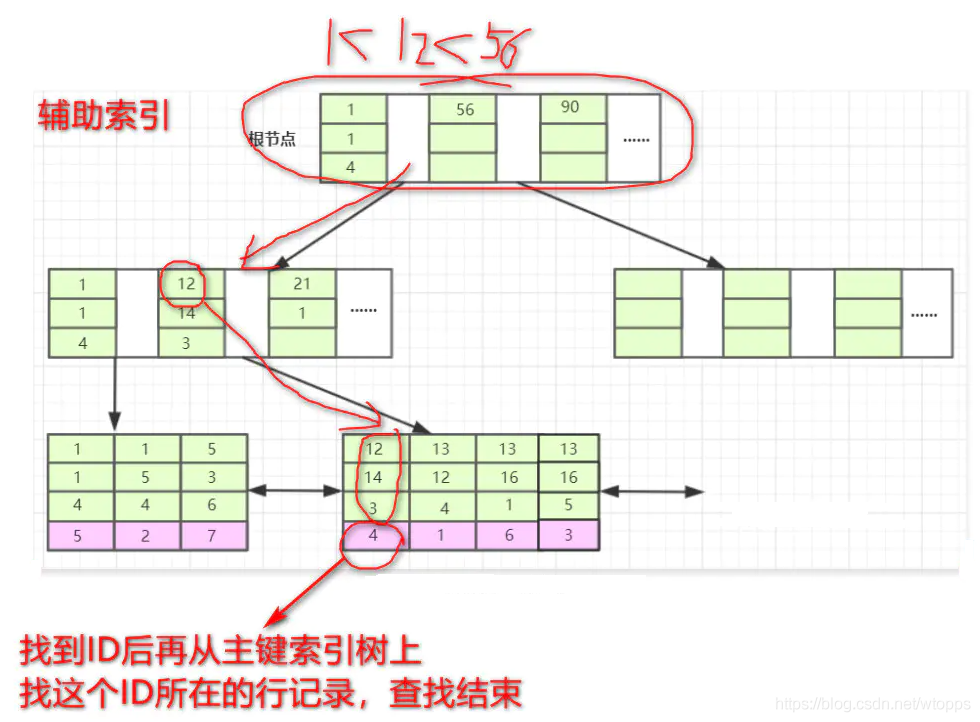
存储引擎首先从根节点（一般常驻内存）开始查找：

第一个索引的第一个索引列为1,12大于1；
第二个索引的第一个索引列为56,12小于56；
于是从这俩索引的中间读到下一个节点的磁盘文件地址，从磁盘上Load这个节点，通常伴随一次磁盘IO，然后在内存里去查找。
当Load叶子节点的第二个节点时又是一次磁盘IO，比较第一个元素，b=12,c=14,d=3完全符合，于是找到该索引下的data元素即ID值，再从主键索引树上找到最终数据。

 

 

最左匹配原则

好了，上面我们了解了联合索引的B+树检索过程，那么再来考虑另一个问题，为什么联合索引会有最左匹配原则？

之所以会有最左前缀匹配原则和联合索引的索引构建方式及存储结构是有关系的。

首先我们创建的c1、c2、c3索引，相当于创建了(c1)、（c1、c2）（c1、c2、c3）三个索引，看完下面你就知道为什么相当于创建了三个索引。
我们看，联合索引是首先使用多列索引的第一列构建的索引树，用上面的例子就是优先使用c1列构建，当c1列值相等时再以c2列排序，若c2列的值也相等则以c3列排序。我们可以取出索引树的叶子节点看一下。

 

 

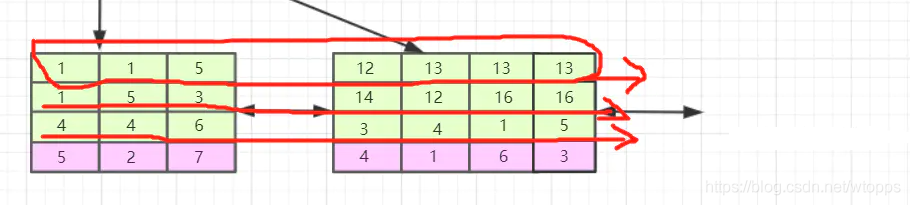
索引的第一列也就是c1列可以说是从左到右单调递增的，但我们看c2列和c3列并没有这个特性，它们只能在c1列值相等的情况下这个小范围内递增，如第一叶子节点的第1、2个元素和第二个叶子节点的后三个元素。
​
由于联合索引是上述那样的索引构建方式及存储结构，所以联合索引只能从多列索引的第一列开始查找。所以如果你的查找条件不包含c1列如（c2, c3）、(c2）、(c3) 是无法应用缓存的，以及跨列也是无法完全用到索引如(c1, c3)，只会用到c1列索引