朴素贝叶斯学习日志——简单案例python计算过程
思路
1、根据贝叶斯公式:P(输出|输入)=P(输入|输出)*P(输出)/P(输入)
2、P(输入)=历史数据中,某个输入占所有样本的比例;
3、P(输出)=历史数据中,某个输出占所有样本的比例;
4、P(输入|输出)=历史数据中,某个输入,在某个输出的数量占所有样本的比例;
题目介绍
有14天的天气数据,以及是否可以打网球的判断,先给出一组天气数据,判断是否可以打网球?
训练数据集:
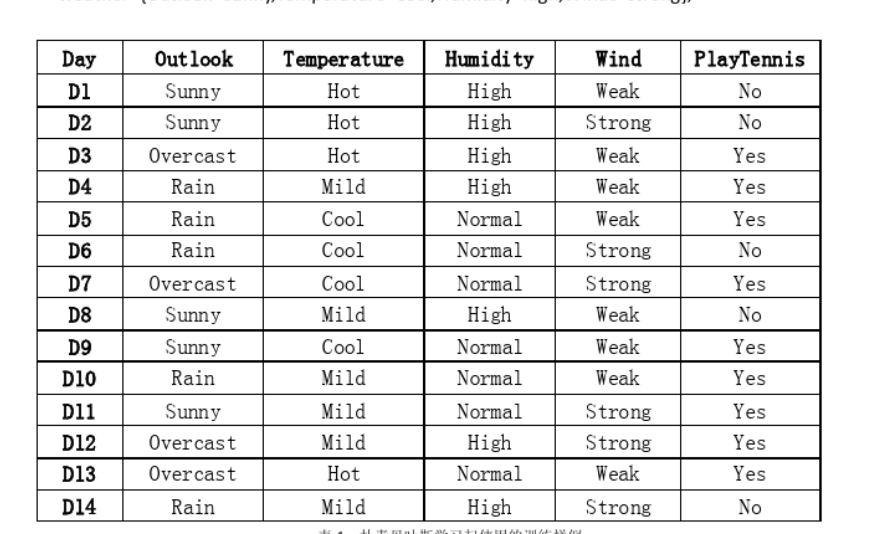
求解问题的数据集:
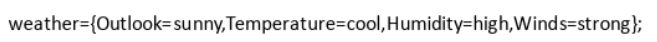
对于以上数据进行简单的的处理:原则是将以上出现的标准用数字进行等级的划分,例如:对于2类数据1表示高,0表示底;对于3类数据2表示高,1表示中等,0表示底。
具体分类以及处理结果如下:
训练数据
sunny:2 overcast:1 rain: 0
hot: 2 mild: 1 cool: 0
high : 1 noraml: 0
strong:1 week: 0
yes: 1 no: 0
S H Hi S YN
day1: 2 2 1 0 : 0
day2: 2 2 1 1 : 0
day3: 1 2 1 0 : 1
day4: 0 1 1 0 : 1
day5: 0 0 0 0 : 1
day6: 0 0 0 1 : 0
day7: 1 0 0 1 : 1
day8: 2 1 1 0 : 0
day9: 2 0 0 0 : 1
day10: 0 1 0 0 : 1
day11: 2 1 0 1 : 1
day12: 1 1 1 1 : 1
day13: 1 2 0 0 : 1
day14: 0 1 1 1 : 0
对于求解数据的数据化简如下:(?表示要求解的数据)
实训数据
2 0 1 1 : ?
代码完成过程
简单介绍一下代码完成的顺序:
1、首先求解先行概率,即p(yes)和p(no)的总体概率;
2、更具要求解的天气数据分别求解其在yes 或 no 的条件下成立的概率;
3、最后求解后验概率,也就是分类标准。
注:在求解第2步概率的时候,为了防止出现0概率,而另其在贝叶斯分类器中占统治地位,将使用m-估计的方法进行概率的求解。
m-估计简单介绍
当我们通过在全部事件的基础上观察某事件出现的比例来估计概率时,例如:P=nc/n.,其中nc为该类别中的样本数量,n为总样本数量。若n=5,当P=0.6时,则nc为3。多数情况下该比例是对概率的一个良好的估计。但当nc很小时估计会较差,例如:P=0.08,样本中同样有5个样例,那么对于nc最可能的取值只有0,。这会导致两个问题:
1、nc/n产生了一个有偏的过低估计概率。
2、当此概率估计为0时,将来的查询此概率项将会在贝叶斯分类器中占统治地位。原因是贝叶斯公式中计算得量其他所有概率项都将乘以此0值。
为了避免此问题,所以需要采用一种估计概率,即如下定义的m-估计:
(nc + m * p) / (n + m)
其中nc为该类别中的样本数量,n为总样本数量,p为将要确定的概率的先验估计,m为等效样本大小的常量。
训练数据存放入数组中
# 训练数据存入数组中
a = np.array([[2, 2, 1, 0, 0], # 1
[2, 2, 1, 1, 0], # 2
[1, 2, 1, 0, 1], # 3
[0, 1, 1, 0, 1], # 4
[0, 0, 0, 0, 1], # 5
[0, 0, 0, 1, 0], # 6
[1, 0, 0, 1, 1], # 7
[2, 1, 1, 0, 0], # 8
[2, 0, 0, 0, 1], # 9
[0, 1, 0, 0, 1], # 10
[2, 1, 0, 1, 1], # 11
[1, 1, 1, 1, 1], # 12
[1, 2, 0, 0, 1], # 13
[0, 1, 1, 1, 0]]) # 14
n = len(a)
求解先验概率
# 先验概率
# 对于总的yes 和 no 的概率
p_yes = 0
p_no = 0
for i in range(n):
if(a[i][4] == 1):
p_yes = p_yes+1
if(a[i][4] == 0):
p_no = p_no+1
n1 = p_yes
n2 = n-n1
p_yes = p_yes / n
p_no = p_no / n
print("p_yes",p_yes,"p_no",p_no,"n",n,"n1",n1,"n-n1",n2)
# 对于其他变量对yes 和 no的概率,即条件概率
# sunny 2 cool 0 high 1 strong 1
psy = 0
psn = 0
pcy = 0
pcn = 0
phy = 0
phn = 0
psty = 0
pstn = 0
for i in range(n):
if(a[i][0]==2 and a[i][4]==1):
psy = psy + 1
if(a[i][0]==2 and a[i][4]==0):
psn = psn + 1
if(a[i][1]==0 and a[i][4]==1):
pcy = pcy + 1
if(a[i][1]==0 and a[i][4]==0):
pcn = pcn + 1
if(a[i][2]==1 and a[i][4]==1):
phy = phy + 1
if(a[i][2]==1 and a[i][4]==0):
phn = phn + 1
if(a[i][3]==1 and a[i][4]==1):
psty = psty + 1
if(a[i][3]==1 and a[i][4]==0):
pstn = pstn + 1
print("nc: ","psy",psy,"psn",psn,"pcy",pcy,"pcn",pcn,"phy",phy,"phn",phn,"psty",psty,"pstn",pstn )
m-估计处理——这里m我取值为14
# 为了解决过低的有偏估计采用m估计计算概率:(nc + m * p) / (n + m)
m = 14
p1 = 1/3
p2 = 1/2
psy = (psy + m * p1) / (n1 + m)
psn = (psn + m * p1) / (n2 + m)
pcy = (pcy + m * p1) / (n1 + m)
pcn = (pcn + m * p1) / (n2 + m)
phy = (phy + m * p2) / (n1 + m)
phn = (phn + m * p2) / (n2 + m)
psty = (psty + m * p2) / (n1 + m)
pstn = (pstn + m * p2) / (n2 + m)
print("psy",psy,"psn",psn,"pcy",pcy,"pcn",pcn,"phy",phy,"phn",phn,"psty",psty,"pstn",pstn )
p_yes = p_yes * psy * pcy * phy * psty
p_no = p_no * psn * pcn * phn * pstn
print("p_yes",p_yes,"p_no",p_no)
最后判断分类
if(p_yes > p_no):
print("yes")
else:
print("no")
结果运行截图

最后我们可以看出,经过该计算过程的运算,系统将求解数据分类为no类型。
小结
1、对于该过程我们证明了分类基本过程可以很好地额实现并完成,但是上述代码仅仅只能是针对以上的类型进行的简单计算,并不具有普遍性,且考虑较为简单,现实中的情况应该更加复杂一点。
2、以上过程中的步骤和计算思想可以移植到其他类型的情况中。
3、对于以上过程,我有一个猜想:每一个情况都有其对应的yes 和 no两种情况,我们可以根据训练数据把每一种情况的概率都计算出来并进行储存。之后用户输入或者选择需要预测的条件,代码更加固定的求解公式求出最终分类答案。
这个固定的公式,举个列子:
p_yes = p_yes * psy * pcy * phy * psty
p_no = p_no * psn * pcn * phn * pstn
就像以上的代码:p(yes)的最终值,为其训练数据中的p(yes)的值乘以其他条件在yes条件下成立的概率。p(no)也可以类似去求解。但是对于该猜想目前没有进行进一步的证实和测试。可能会在后续进行证实。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号