题解：P2013 无线电测向

P2013 无线电测向

题目省流：求两条直线交点坐标

使用样例数据作出下图：

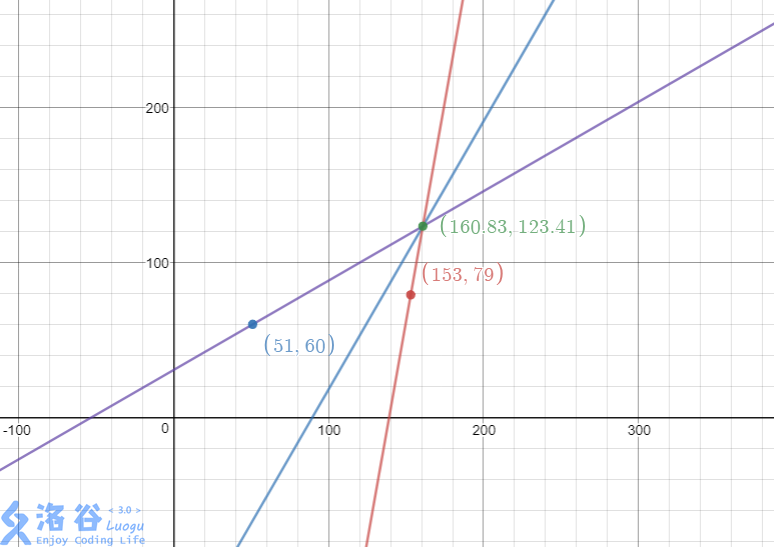
（图片来自@_MRCMRC_）

图中红线和紫线为灯塔与船的连线，蓝线为船的航线。

由输入可以知道灯塔 A、B 相对于 \(x\) 正半轴的角度 \(\theta_A\)、\(\theta_B\)（逆时针方向） 和它们分别的坐标 \((x_A, y_A)\)、\((x_B, y_B)\)。

设灯塔 A 与船的连线为 \(l_1: y = k_Ax + b_A\)，灯塔 B 与船的连线为 \(l_2: y = k_Bx + b_B\)。

我们用待定系数法，先用 \(\tan\) 求出 \(k_A\)，有

\[k_A = \frac{\Delta y}{\Delta x} = \tan \theta_A \]

再代入 \(x = x_A, y = y_A\)，解一元一次方程

\[y = k_Ax + b_A \]

\[\to y_A = k_Ax_A + b_A \]

\[\to b_A = y_A - k_Ax_A \]

所以得出 \(l_1\) 的表达式 \(y = k_Ax + b_A\)（这里 \(k_A\) 和 \(b_A\) 已求得）。

同理，我们可以求出 \(l_2\) 的表达式 \(y = k_Bx + b_B\)，其中 \(k_B = \tan \theta_B\)，\(b_B = y_B - k_Bx_B\)。

接下来求交点坐标，因为交点既在 \(l_1\) 上也在 \(l_2\) 上，所以联立两个表达式得出方程：

\[ \left\{ \begin{array}{ll} y = k_Ax + b_A \textcircled{1}\\ y = k_Bx + b_B \textcircled{2} \end{array} \right. \]

\(\textcircled{2} - \textcircled{1}\)：

\[b_A - b_B = (k_B - k_A)x \]

解得

\[ \left\{ \begin{array}{ll} x = \frac{b_A - b_B}{k_B - k_A}\\ y = k_Ax + b_A \end{array} \right. \]

求得交点 \((x, y)\)，即船的坐标。

还有记得转弧度制！！！

AC Code:

#include <bits/stdc++.h>

using namespace std;

const double pi = 3.1415926535;

struct beacon // 灯塔
{
    string name;
    double x, y;
};

int main()
{
    int n;
    cin >> n;
    beacon a[n];
    for (int i = 0; i < n; ++i)
    {
        cin >> a[i].name >> a[i].x >> a[i].y;
    }
    double ship_angle, angle1, angle2;
    beacon beacon1, beacon2;
    cin >> ship_angle >> beacon1.name >> angle1 >> beacon2.name >> angle2;
    for (int i = 0; i < n; ++i)
    {
        if (a[i].name == beacon1.name)
        {
            beacon1 = a[i];
        }
        if (a[i].name == beacon2.name)
        {
            beacon2 = a[i];
        }
    }
    angle1 += ship_angle;
    angle2 += ship_angle;

    double k1 = tan((90 - angle1) * pi / 180);
    double b1 = beacon1.y - k1 * beacon1.x;
    double k2 = tan((90 - angle2) * pi / 180);
    double b2 = beacon2.y - k2 * beacon2.x;

    double x = (b2 - b1) / (k1 - k2);
    double y = k1 * x + b1;
    printf("%.2lf %.2lf", x, y);
    return 0;
}