0717果苣之手

简要题意：

一副牌有n张，编号为1,2,...,n。初始阶段牌按顺序排列（即位于i号未知的牌恰好是i号牌）。

我们会进行m次洗牌，每次洗牌会将原本位于位置i的牌洗到p_i，而p₁,p₂,...,p_n构成了一个排列

问最后发牌时的顺序。

分析：

由于pi是1到n的一种排列，所以我们可以知道：

洗牌，是有很多个环的！

换句话说，i号位置最后是哪张牌，在其构成的环内，有周期性。

 

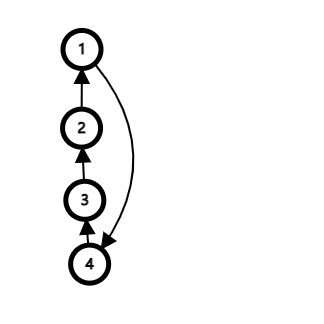
以上图为例，n=4;p1=2;p2=3;p3=4;p4=1

经过一次洗牌，1号会换到4处，2号会换到1处，以此类推。

所以，它的周期为环内点的个数：4

我们处理时，只需要把每个这样的环单独处理，将 m%周期，然后DFS

 

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=3e5+5;
int n, sum[N], fa[N];
int getf(const int x)
{
    if(fa[x]==x)return x;
    return fa[x]=getf(fa[x]);
}
int getnet,father,gt[N],to[N],Ans[N],check[N];
void DFS(const int x,const int id)
{
    check[x]=1;gt[id]=x;
    if(!check[to[x]])DFS(to[x],id+1);
    int tmp=id+getnet;if(tmp>sum[father])tmp-=sum[father];
    Ans[x]=gt[tmp];
}
char rdin[N];
map<int,int>mp;
signed main()
{
    scanf("%d",&n);scanf("%s",&rdin[1]);rdin[0]='0';
    for(re i=1;i<=n;++i)fa[i]=i,sum[i]=1;
    for(re i=1;i<=n;++i)
    {
        int x;scanf("%d",&x);to[x]=i;
        int f1=getf(i),f2=getf(x);
        if(f1!=f2)fa[f1]=f2,sum[f2]+=sum[f1];
    }
    for(re i=1;i<=n;++i)
    if(!check[i])
    {
        getnet=0;father=getf(i);
        if(!mp.count(sum[father]))
        {
            int tmp=0;
            for(re j=1,len=strlen(rdin)-1;j<=len;++j)
            tmp=((tmp<<1)+(tmp<<3)+(rdin[j]-'0'))%sum[father];
            mp[sum[father]]=tmp;
        }
        getnet=mp[sum[father]];
        DFS(i, 1);
    }
    for(re i=1;i<=n;++i)printf("%d ",Ans[i]);
    return 0;
}

 

值得注意的是，m<=10¹⁰⁰⁰⁰⁰，对此我们只需要像“快读”一样，处理一下即可！

 

“读题马虎一时，爆零心痛一世！”----《kzsn语录》kzsn