全连接层到卷积层

从全连接层到卷积

我们之前讨论的多层感知机十分适合处理表格数据，其中行对应样本，列对应特征。 对于表格数据，我们寻找的模式可能涉及特征之间的交互，但是我们不能预先假设任何与特征交互相关的先验结构。 此时，多层感知机可能是最好的选择，然而对于高维感知数据，这种缺少结构的网络可能会变得不实用。

例如，在之前猫狗分类的例子中：假设我们有一个足够充分的照片数据集，数据集中是拥有标注的照片，每张照片具有百万级像素，这意味着网络的每次输入都有一百万个维度。 即使将隐藏层维度降低到1000，这个全连接层也将有 \(10^6 * 10^3 = 10^9\) 个参数。 想要训练这个模型将不可实现，因为需要有大量的GPU、分布式优化训练的经验和超乎常人的耐心。

不变性

平移不变性

不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”

局部性

神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

多层感知机的限制

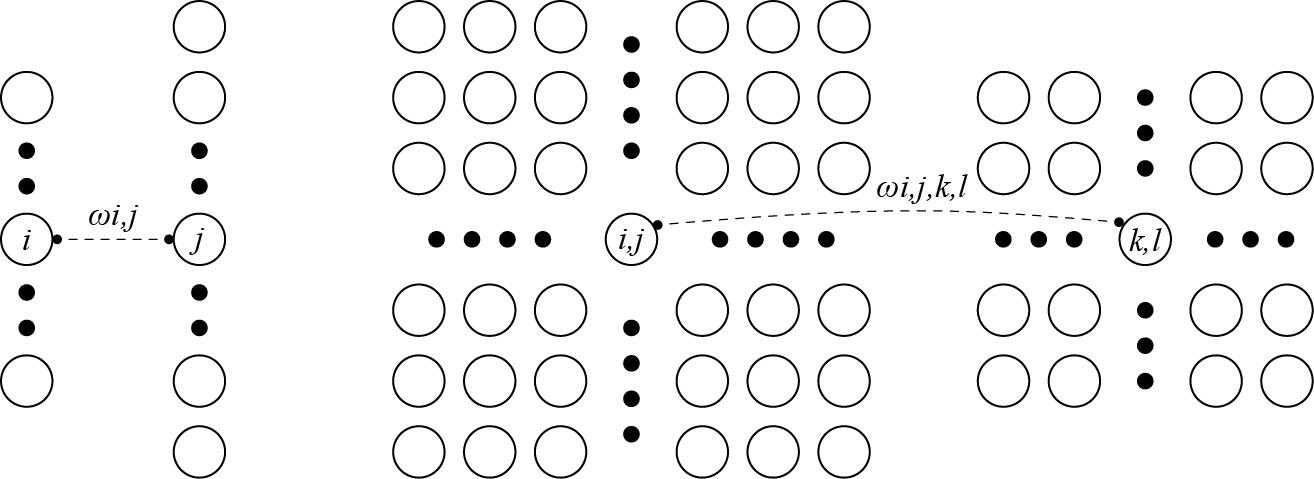
假设多层感知机的输入是\(X\),将其隐藏表示记为\(H\),使用 \([X]_{i,j}\) 和 \([H]_{i,j}\) 表示 \((i,j)\) 位置上的像素点。
因为每个像素点都需要和其他像素点联系，故每个像素点都需要一个二阶的权重张量，又由于是二维图像，故最终权重张量 \(W\) 为四维。
再假设偏置参数为 \(U\) ，则可以将全连接层表示为：

\[ [H]_{i,j} = \sum_{k,l} [X]_{k,l} \cdot [V]_{i,j,k,l} + [U]_{i,j} \]

为了方便表示，我们对下标 \((k,l)\) 进行重新索引，使得 \(k = i + a, l = j + b\),则可以得到重排的权重矩阵 \([V]_{i,j,a,b} = [W]_{i,j,i+a,j+b}\)

即上述可表述为公式：

\[ [H]_{i,j} = \sum_{a,b} [X]_{i+a,j+b} \cdot [V]_{i,j,a,b} + [U]_{i,j} \]

1.平移不变性

现在引入平移不变性，即检测对象在输入 \(X\)中的平移应该仅导致隐藏表示 \(H\) 中的平移。简言之，无须每个像素都要独享一个二维权值张量，所有像素共享同一个即可，故权重张量降为二维即可。此时式子可以简化为：

\[ [H]_{i,j} = \sum_{a,b} [X]_{i+a,j+b} \cdot [V]_{a,b} + u \]

这就是所谓卷积，使用系数 \([V]_{a,b}\) 对 \((i+a, j+b)\) 附近的像素 \([H]_{i,j}\) 进行加权得到。

2.局部性

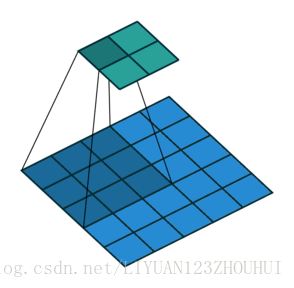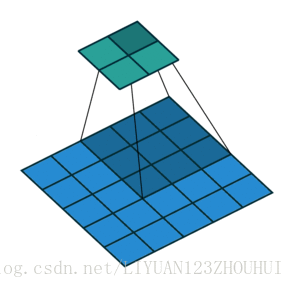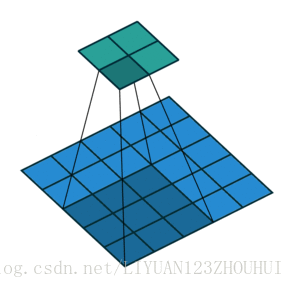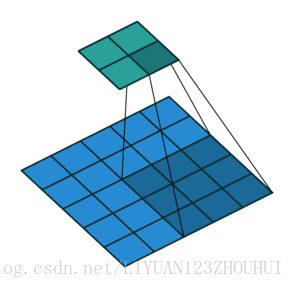
对于上述的 \(a, b\) 不应该取太大，即范围不应太大，至少不应该是全图。故可将 \(|a| > \Delta,|b| > \Delta\) 的范围设置为0（即不考虑范围外的影响）。故可将式子重写为：

\[ [H]_{i,j} = \sum_{a,b}^\Delta [X]_{i+a,j+b} \cdot [V]_{a,b} + u \]

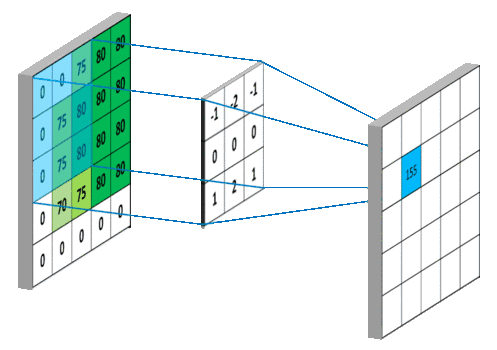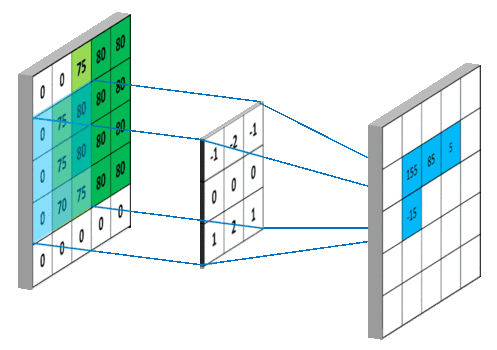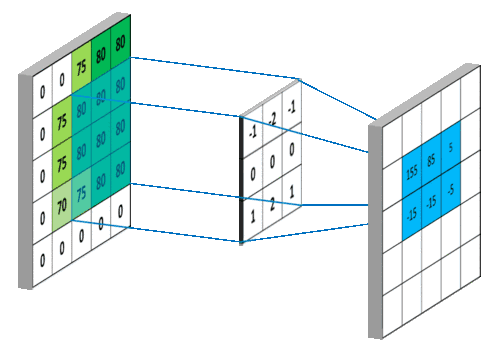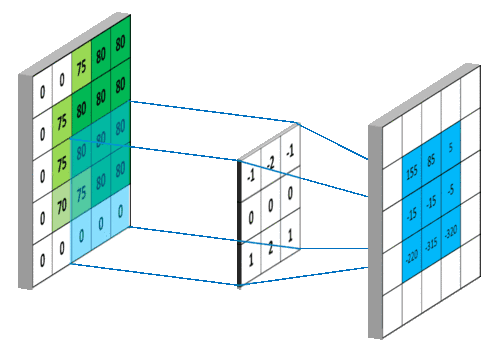
具体如图所示