数论复习

. 质数

质数判断

1.试除法

bool is_prime(int n)
{
    if(n < 2) return false;
     for(int i = 2;i*i <= n;i++)
         if(n%i == 0) return false;
     return true;
}

 有一些效率更高的随机性算法，不过水平超出了我们的范畴，不再讨论。

另外 大数判断 Miller-rabin算法，不提了。

2.筛法

埃拉托斯特尼筛法，埃氏筛法（Eratosthenes）

我们可以从2开始， 由小到大扫描每个数x，它的倍数 2x，3x，....，[N/x] * x 标记为合数。

当扫描到一个数时，若它尚未被标记，则它不能被2~x - 1之间的任何数整除，该数就是质数。

该算法实现简单，效率已经非常接近于线性，是算法竞赛中最常用的质数筛法。

时间复杂度为：O（NloglogN）；

void primes(int n)
{
    memset(vis, 0, sizeof(vis));
    for(int i = 2;i <= n;i++)
    {
        if(vis[i]) continue;
        printf("%d\n", i); //i是质数
        for(int j = i;j <= n/i;j++) vis[i*j] = 1; 
    }
}

再来介绍一种更优的算法：线性筛（欧拉筛法）

算法思想：通过"从大到小累积质因子"的方式标记每个合数，设数组 v 记录每个数的最小质因子，我们按以下步骤维护 v；

　 1.依次考虑 2~N 之间的每一个 i.

　 2.若v[i] = i, 说明 i 是质数， 把它保存下来。

　 3.扫描不大于 v[i] 的每个质数， 令 v[i*p] = p. 也就是在 i 的基础上累积一个质因子 p，因为 p <= v[i]，所以p就是合数 i*p 的最小质因子。

这样就可以在线性时间内找到素数了！ 时间复杂度为O（n）。

void primes(int n)
{
    memset(v, 0, sizeof(v));//最小质因子 
    int m = 0;//质数数量
    for(int i = 2;i <= n;i++)
    {
        if(v[i] == 0)
        {
            v[i] = i;
            prime[++m] = i;//i是质数 
        }
        //给当前的数i乘上一个质因子
        for(int j = 1;j <= m;j++)
        {
            // i有比prime[j]更小的质因子,或者超出n的范围,停止循环。
            if(prime[j] > v[i] !! prime[j] > n/i) break;
            //prime[j]是合数i*prime[j]的最小质因子
            v[i*prime[j]] = prime[j]; 
        } 
    } 
}

质因数分解（分解为质因数）

#include<iostream>
#include<vector>
#include<cstdio>
using namespace std;

const int N = 100005;
vector<int > factor[N];

void init()
{
    int tmp;
    for(int i = 2; i < N; i++)
    {
        if(factor[i].size() == 0)
        {    
            for(int j = i; j < N; j += i)
            {
                tmp = j;
                while(temp % i == 0)
                {
                    factor[i].push_back(i);
                    tmp /= i;
                }
            }
        }
    }
}

卢卡斯定理

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,p,T;
ll ksm(ll x,ll y){
    ll res=1;
    while(y){
        if(y&1) res=(res*x)%p;
        x=x*x%p;
        y>>=1;
    }
    return res;
}
ll C(ll x,ll y){
    //if(!y) return 1;
    if(x<y) return 0;
    ll s1=1,s2=1;
    for(int i=x-y+1;i<=x;i++) s1=s1*i%p;
    for(int i=1;i<=y;i++) s2=s2*i%p;
    return s1*ksm(s2,p-2)%p;
}
ll lucas(ll x,ll y){
    if(! y) return 1;
    return C(x%p,y%p)*lucas(x/p,y/p)%p;
}
int main()
{
    scanf("%lld",&T);
    while(T--){
        scanf("%lld%lld%lld",&n,&m,&p);
        printf("%lld\n",lucas(n+m,m));
    }
    return 0;
}

欧拉函数

1、埃拉托斯特尼筛求欧拉函数

观察欧拉函数的公式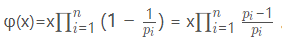， 。我们用phi[x]表示φ(x)。可以一开始把phi[x]赋值为x，然后每次找到它的质因数就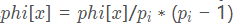（先除再乘，避免溢出）。当然，若只要求一个数的欧拉函数，可以从1到sqrt(n)扫一遍，若gcd(i,n)=1就更新phi[n] phi[n]phi[n]。复杂度为O(logn)（代码就不给了）。那要求1~n所有数的欧拉函数呢？可以用埃拉托斯特尼筛的思想，每次找到一个质数，就把它的倍数更新掉。这个复杂度虽然不是O(n)，但还是挺快的（据说是O(n*ln ln n)，关于证明，可以点这里，虽然我看不懂）。

2. 欧拉筛求欧拉函数

前提是要懂欧拉筛。每个数被最小的因子筛掉的同时，再进行判断。i表示当前做到的这个数，prime[j]表示当前做到的质数，那要被筛掉的合数就是i*prime[j]。若prime[j]在这个合数里只出现一次（i%prime[j]!=0），也就是i和prime[j]互质时，则根据欧拉函数的积性函数的性质，phi[i * prime[j]]=phi[i] * phi[prime[j]]。若prime[j]在这个合数里出现了不止一次（i%prime[j]=0），也就是这个合数的所有质因子都在i里出现过，那么根据公式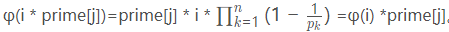，复杂度为O(n)。

#include<bits/stdc++.h>
using namespace std;
const int N=100000;
int b[N],prime[N],phi[N];
int eular1(int n){
    //φ(n)=n*(1-1/p1)*(1-1/p2)*(1-1/p3)*(1-1/p4)…..(1-1/pn), 其中pi为n的质因数;
    int ans=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            ans=ans-ans/i;
            while(n%i==0)
                n/=i;
        }
    }    
    if(n>1) ans=ans-ans/n;
    return ans;
}
void eular2(int n){
    for(int i=1;i<=n;i++) phi[i]=i;
    for(int i=2;i<=n;i++){
        if(phi[i]==i){
            for(int j=i;j<=n;j+=i)
                phi[j]=phi[j]/i*(i-1);
        }
    }
}
void eular3(int n){
    phi[1]=1; 
    int num=0;
    for(int i=2;i<=n;i++){
        if(b[i]==0){//这代表i是质数 
            prime[++num]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=num&&prime[j]*i<=n;j++){
            b[i*prime[j]]=1;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else phi[i*prime[j]]=phi[i]*phi[prime[j]];
                //phi[ i*prime[j] ] = phi[i] * (prime[j]-1); 

        }
    }
}
int main()
{
    
    return 0;
}

乘法逆元

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,p,inv[3000005];
/*ll ksm(ll a,ll b){
    ll res=1;  a%=p; //b%=p;
    while(b){
        if(b&1) res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res%p;
}*/
int main()
{
    scanf("%lld%lld",&n,&p);
    /*for(int i=1;i<=n;i++)
        printf("%lld\n",ksm(i,p-2));*/
//线性递推
    inv[0]=0; inv[1]=1;
    puts("1");
    for(int i=2;i<=n;i++){
        inv[i]=(ll)p-(p/i)*inv[p%i]%p;
        printf("%lld\n",inv[i]);
    }
    return 0;
}