强化学习笔记（一）基本概念

前言

近两年AIGC模型均在SFT之后，进行强化学习的微调，并逐渐成为主流范式，因此，记录一下学习强化学习的笔记，以供回顾。本笔记参考https://www.bilibili.com/video/BV1sd4y167NS。

基本概念

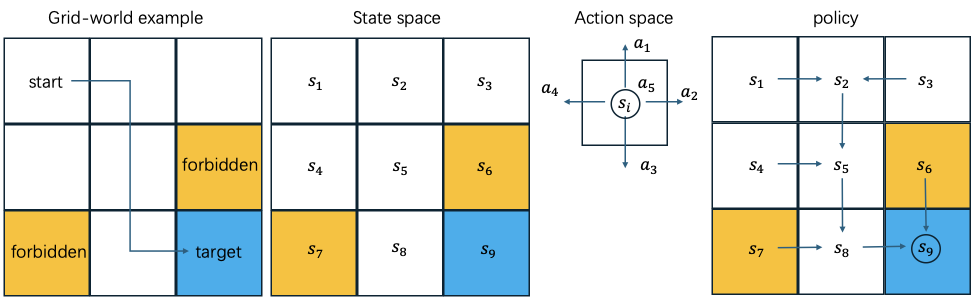
以grid-world game为例，结合上图，给出强化学习中的一些基础概念。

grid-world game

给定一个出发点start和一个目标点target，为机器人找出一条从start到target的好的路径。其中，forbidden表示禁止进入的区域或风险大的区域。

state

智能体相较于环境的状态称为state。对应于机器人所处的位置\(s_{i}\)。

state space

智能体所有状态所组成的集合称为state space。对应于机器人的可能处在的9个位置，\(\mathcal{S}=\{s_{i}\}_{i=1}^{9}\)。

action

智能体某个状态下的行动称为action。对应于机器人在\(s_{i}\)处朝某一方向移动。

action space

智能体某个状态下的所有行动组成的集合称为action space，是state的函数。智能体在不同state下可能存在不同的action space，例如饿了会想着吃饭而吃饱之后不会继续进食。对应于机器人向上，向下，向左，向右和静止五个行动。\(\mathcal{A}(s_{i})=\{a_{i}\}_{i=1}^{5}\)。

state transition

智能体采取一个action后，由一个state转移到另一个state的过程，称为state transition。对应于\(s_{1} \xrightarrow{a_{2}} s_{2}\)。可以采用state transition probability \(p(s_{j} | s_{i}, a_{k})\)表示。例如上图，\(p(s_{2}|s_{1}, a_{2})=1\)，\(p(s_{2}|s_{1}, a_{i\neq2})=0\)。

policy

policy给出智能体在某个state时，需要采取的action。可用\(\pi(a_{j} | s_{i})\)表示。例如上图，\(\pi(a_{2}|s_{1})=1\)，\(\pi(a_{i\neq2}|s_{1})=0\)，\(\pi(a_{3}|s_{2})=1\)，\(\pi(a_{i\neq3}|s_{2})=0\)。

reward

智能体在执行完某action后得到的数值。正数代表鼓励该action，负数代表抵制该action。例如在grid-world example中，可以定义，当机器人试图越界时，reward为-1，\(r(s_{1}, a_{1})=-1\)。当机器人抵达target处，reward为+1，\(r(s_{8}, a_{2})=1\)。当机器人试图进入forbidden时，reward为-1，\(r(s_{5}, a_{2})=-1\)。其余action对应的reward为0，\(r(s_{5}, a_{3})=0\)。

trajectory

state-action-reward链称为trajectory。如\(s_{1} \xrightarrow[r=0]{a_{2}} s_{2} \xrightarrow[r=0]{a_{3}} s_{5} \xrightarrow[r=0]{a_{3}} s_{8} \xrightarrow[r=1]{a_{2}} s_{9}\)。

return

某一trajectory的reward总和称为return。如\(s_{1} \xrightarrow[r=0]{a_{2}} s_{2} \xrightarrow[r=0]{a_{3}} s_{5} \xrightarrow[r=0]{a_{3}} s_{8} \xrightarrow[r=1]{a_{2}} s_{9}\)，该trajectory的return为\(0+0+0+1=1\)。

discounted return

某一trajectory的return有可能是无限的，如$s_{1} \xrightarrow[r=0]{a_{2}} s_{2} \xrightarrow[r=0]{a_{3}} s_{5} \xrightarrow[r=0]{a_{3}} s_{8} \xrightarrow[r=1]{a_{2}} s_{9} \xrightarrow[r=1]{a_{5}} s_{9} \xrightarrow[r=1]{a_{5}} s_{9} \dots $，此时计算得到的return是发散的。为了处理这种情况，引入了discounted rate \(\gamma \in (0, 1)\)，每执行一次action后，得到的reward需要乘以该系数。此时，上述的return调整为\(0+0+0+\gamma^{3}+\gamma^{4}+\gamma^{5}+\dots=\gamma^{3}(1+\gamma+\gamma^{2}+...)=\frac{\gamma^{3}}{1-\gamma}\)。

episode

若某trajectory存在某些terminal states，则该trajectory称为一个episode。例如，\(s_{1} \xrightarrow[r=0]{a_{2}} s_{2} \xrightarrow[r=0]{a_{3}} s_{5} \xrightarrow[r=0]{a_{3}} s_{8} \xrightarrow[r=1]{a_{2}} s_{9}\)是一个episode。

Markov Decision Process (MDP)

MDP由以下要素组成

1. sets
   State：\(\mathcal{S}\)，表示state的集合。
   Action：\(\mathcal{A}(s), s\in \mathcal{S}\)，表示某state下action的集合。
   Reward：\(\mathcal{R}(s, a)\)，表示某state下，执行action后得到reward的集合。
2. probability
   state transition probability：\(p(s'|s, a)\)，表示在state \(s\)下，执行action \(a\)后，转移至state \(s'\)的概率。
   reward probability：\(p(r|s, a)\)，表示在state \(s\)下，执行action \(a\)后，得到reward \(r\)的概率。
3. policy
   state \(s\)下，执行action \(a\)的概率\(\pi(a|s)\)。
4. markov property
   \(p(s_{t+1}|s_{t}, a_{t+1}, s_{t-1}, a_{t}, \dots, s_{0}, a_{1})=p(s_{t+1}|s_{t}, a_{t+1})\)
   \(p(r_{t+1}|s_{t}, a_{t+1}, s_{t-1}, a_{t}, \dots, s_{0}, a_{1})=p(r_{t+1}|s_{t}, a_{t+1})\)
   第\(t+1\)时刻的state只和第\(t\)时刻的state \(s_{t}\)与所要采取的action \(a_{t+1}\)有关。

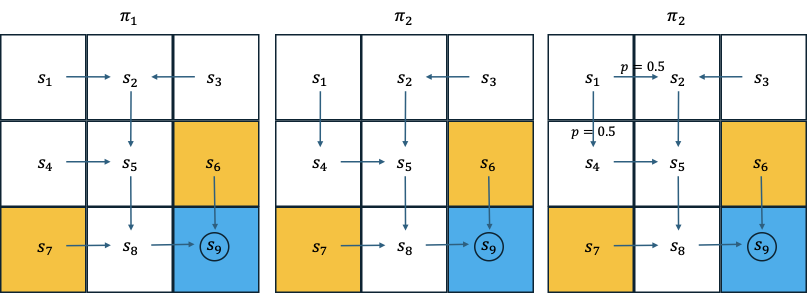
当policy \(\pi\)确定后，markov decision process退化为markov process。上述每一个策略\(\pi_{i}\)下的grid-world game均为markov process，将策略\(\pi_{i}\)同时纳入考虑中，markov process转变为markov decision process。