常见的十大排序算法
优劣术语
- 稳定性 原本a在b前,a=b,排序之后位置任然不变。不稳定性则相反
- 内排序 所有排序都在内存中完成。外排序数据放磁盘,排序通过磁盘内存的数据传输
- 时间复杂度 算法执行耗费的时间
- 空间复杂度 算法执行耗费的内存
1.冒泡排序法
原理:比较两个相邻的元素,将值大的元素交换至右端。
如:9 3 7 5 8 6 4 3 1 2
1.循环次数就是 n-1在这里是10-1=9
2.第一轮比较
第一次比较:9 比3 大,3 9 7 5 8 6 4 3 1 2
第二次比较:9 比7 大,3 7 9 5 8 6 4 3 1 2
第三次比较:9 比5 大,3 7 5 9 8 6 4 3 1 2
第四次比较:9 比8 大,3 7 5 8 9 6 4 3 1 2
第五次比较:9 比6 大,3 7 5 8 6 9 4 3 1 2
第六次比较:9 比4 大,3 7 5 8 6 4 9 3 1 2
第七次比较:9 比3 大,3 7 5 8 6 4 3 9 1 2
第八次比较:9 比1 大,3 7 5 8 6 4 3 1 9 2
第九次比较:9 比2 大,3 7 5 8 6 4 3 1 2 9
第一轮比较完成:共比较n-1=9次,最大的元素9排在最后了
2.第二轮比较:n-1-1次
第一次比较:3 比7小不需要动,3 7 5 8 6 4 3 1 2 9
第二次比较:7 比5 大,3 5 7 8 6 4 3 1 2 9
第三次比较:7 比8小不需要动,3 5 7 8 6 4 3 1 2 9
第四次比较:8 比6 大,3 5 7 6 8 4 3 1 2 9
第五次比较:8 比4 大,3 5 7 6 4 8 3 1 2 9
第六次比较:8 比3 大,3 5 7 6 4 3 8 1 2 9
第七次比较:8 比1 大,3 5 7 6 4 3 1 8 2 9
第八次比较:8 比2大, 3 5 7 6 4 3 1 2 8 9
第二轮比较完成:共比较n-1-1=8次,最大的元素8和9排在最后了,红色的表示本身已经是最大的不需要比较了
3.第3轮:3 5 6 4 3 1 2 7 8 9
4.第4轮:3 5 4 3 1 2 6 7 8 9
5.第5轮:3 4 3 1 2 5 6 7 8 9
6.第6轮:3 3 1 2 4 5 6 7 8 9
7.第7轮:3 1 2 3 4 5 6 7 8 9
8.第8轮:1 2 3 3 4 5 6 7 8 9
9.第9轮比较:n-1-1次
第一次比较:1 比2小不需要动,1 2 3 3 4 5 6 7 8 9
第9轮比较完成:共比较n-1-8=1次,最大的元素排在最后了且是有序的,红色的表示本身已经是最大的不需要比较了
中间的 3 - 8轮依此类推
总结:轮询了n-1次, 比较次数 n-1-0 , n-1-1 ... n-1-9,
比较了(n-1)(n-2)/2 ,时间复杂度 O(n2)
/** * 原理:比较两个相邻的元素,将值大的元素交换到右边 * 1.每次拿一个元素去跟其他的元素比较和交换 * 2.下一次需要比较的元素个数就是 n-i-1( 0<=i<n-1)
* 3.每次有i个元素在最后是最大的且是排好序的 * @param list */ public static void bubbleSort(List<Integer> list) { if (null == list || list.size() <2){ return; } // list.size-1: 这里是因为不要和自己比较,所有每次需要比较n-1个元素 for (int i = 0; i < list.size()-1; i++) { // size-i-1:每次最后i个元素就是最大了,不需要比较了 for (int j = 0; j < list.size() - 1 - i; j++) { if (list.get(j) > list.get(j + 1)){ int temp = list.get(j); list.set(j,list.get(j + 1)); list.set(j + 1,temp); } } } }
2.选择排序
原理:每一趟从待排序的记录中选出最小的元素,顺序放在已排好序的序列最后,直到全部记录排序完毕
比较次数 n-1, n-1-1, n-1-2 ... n-1-i
需要 (n-1)(n-2)/2,时间复杂度O(n2)
/** * 选择排序原理:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。 * 1.每次拿待排序元素的第一个元素同待排序的其他元素比较寻找最小值 * 2.交换待排序元素的第一个元素和最小元素的位置 * * @param list */ public static void selectSort(List<Integer> list) { if (null == list || list.size() < 2){ return; } for (int i = 0; i < list.size(); i++) { int minIndex = i; // 待排序的第一个元素 int min = list.get(minIndex); // j=i+1:比较除了自己以外的待排序元素 for (int j = i + 1; j < list.size() ; j++) { // 每次取待排序的元素的第一个同剩下的待排序元素比较寻找最小元素 if (min > list.get(j)) { minIndex = j; } } // 将待排序的最小元素与待排序的第一个元素交换位置 int temp = list.get(i); if (temp > min) { list.set(i, min); list.set(minIndex, temp); } } }
3.插入排序
原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
/** * 插入排序原理:每一步将一个待排序的数据插入到前面已经排好序的有序序列中并形成有序序列,直到插完所有元素为止 * 1.第一个元素就一个肯定是有序的 * 2.每次从待排序元素中取出第一个元素插入到前面的有序序列中并形成新的有序序列 * @param list */ public static void insertSort(List<Integer> list) { if (null == list || list.size() < 2){ return; } // list.size()-1: 每次都是从待排序元素的第一个插入到有序序列中形成有序序列,对应下面的j=i+1 for (int i = 0; i < list.size() - 1; i++) { for (int j = i + 1; j > 0; j--) { if (list.get(j) < list.get(j - 1)) { int temp = list.get(j); list.set(j, list.get(j - 1)); list.set(j - 1, temp); } } } }
4.希尔排序
原理:
希尔排序又称缩小增量排序,是对插入排序的改进
选取一个小于数组长度n的值m1为增量,形成m1个子数组,对子数组进行插入排序;
缩小增量为m2,形成m2个子数组,对子数组进行插入排序;
不断缩小增量进行排序,最终将增量缩小为1,整个数组排序完成
最坏的是O(n2)
/** * 希尔排序原理:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。 * 1.将原数据分成多个组分别,每个组间进行插入排序 * 2.缩小增量也就是步长,再重复步骤一,直到增加为1,排序完成 * @param list */ public static void shellSort(List<Integer> list) { if (null == list || list.size() < 2){ return; } // gap=list.size()/2 初始增量,gap/=2 缩小增量 for (int gap = list.size()/2; gap > 0 ; gap/=2) { for (int i = gap; i < list.size(); i++) { int j = i - gap; // 这里是交替进行交换的,可以每次都对同一个组的插入排序 // 比如现在有数字 7 4 9 8 3 5 6 1,增加为2 ; 7 9 3 6 一组, 2 8 5 1 一组 // 分解 i = 3时, 4 8 进行插入排序 // i = 4时,7 9 3 进行插入排序 // i=5时, 4 8 5 进行插入排序 // i=6时, 7 9 3 6 进行插入排序 // i=时, 4 8 5 1 进行排序 // 接着进行下一路排序,增量为1,也就是步长1,就时一组了,进行一次插入排序 while (j >= 0 && list.get(j) > list.get(j+gap)) { int temp = list.get(j); list.set(j, list.get(j+gap)); list.set(j + gap, temp); j -= gap; } } } }
5.归并排序
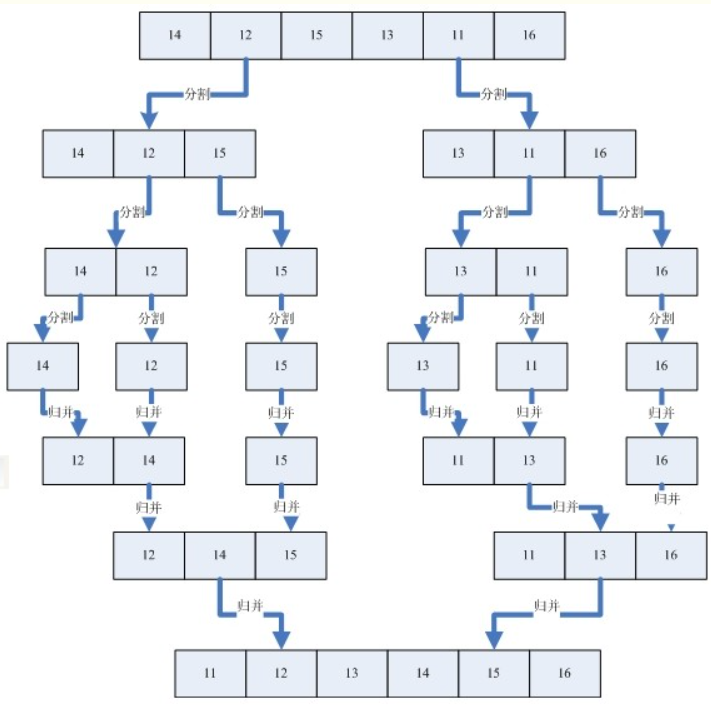
原理:将数组拆分成多个小组,直到只有一个元素结束,然后一次两两合并排序
例如:两个小数组 A={1,3 ,7} B={1,5 ,9}
1)A的1等于B的1,将A的1放入临时数组temp{1},A的指针往右移一位
2)比较A的3和B的1,A的3大于B的1,将B的1放入临时数组temp{1,1}, B的指针往右移一位
3)比较A的3和B的5,A的3小于B的5,将A的3放入临时数组temp{1,1,3}, A的指针往右移一位
4)比较A的7和B的5,A的7大于B的5,将B的5放入临时数组temp{1,1,3,5}, B的指针往右移一位
5)比较A的7和B的9,A的7小于B的8,将A的7放入临时数组temp{1,1,3,5,7}, 此时A的指针往右移一位已经大于A的数组最大索引,结束比较
6)将B剩余的元素一次放入temp中emp{1,1,3,5,7,9},然后将临时数组的元素按照原来的元素的起止位置复制回去
/** * 1)尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数是 * 1为止。 * (2)将相邻的两个子组进行合并成一个有序的大组 * (3)不断的重复步骤2,直到最终只有一个组为止。 */ public class MergeSort { public static void sort(Integer[] array) { if (null == array || array.length < 2){ return; } Integer[] temp = new Integer[array.length]; sort(array,0,array.length - 1,temp); } private static void sort(Integer[] array, int left, int right, Integer[] temp) { if (left < right) { int mid = (left + right)/2; sort(array,left,mid,temp); sort(array,mid + 1,right,temp); mergeSort(array,left,mid,right,temp); } } /** * 每次把左右的数据排序后放入temp中,然后把这部分的数据再复制回原数组 * 比如: 4 5 和 3 7 ,以 3 4 5 7 放入temp,然后复制会原数组的四个位置 * @param array * @param left * @param mid * @param right * @param temp */ private static void mergeSort(Integer[] array, int left, int mid, int right, Integer[] temp) { int i = left; int j = mid + 1; int t = 0; while (i <= mid && j<=right) { if (array[i] <= array[j]) { temp[t++] = array[i++]; } else { temp[t++] = array[j++]; } } // 比较完左边剩余的较大的元素:有序的 while (i <= mid) { temp[t++] = array[i++]; } // 比较完右边剩余的较大的元素:有序的 while (j <= right) { temp[t++] = array[j++]; } t = 0; while (left <= right) { array[left++] = temp[t++]; } } }
7.快速排序
原理:选取一个基数,小于基数的放左边,大于基数的放右边,递归处理左右两边的数据,直到排序完成
快数排序可以右很多实现方式:双指针只是其中一中(例如简单快速排序:使用消耗内存的方式,大于等于基数的放到一个集合,小于基数的放到一个集合,然后分别使用插入排序或者选择排序,最后合并成一个集合)
不想画图借用别人的图
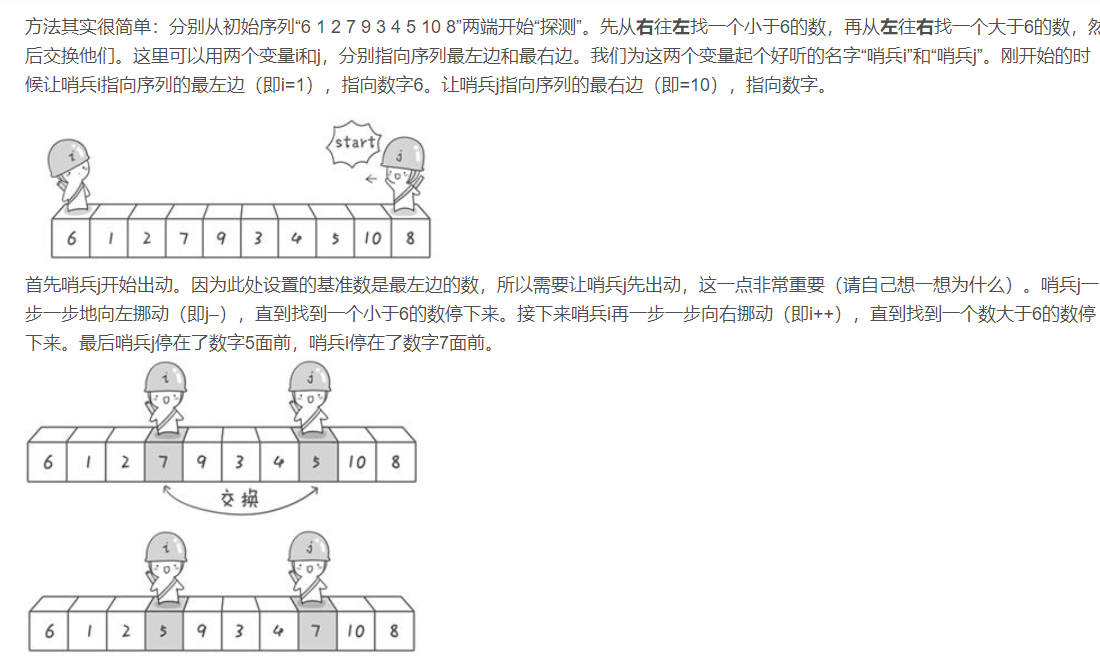

实现思路:
1.第一个元素为基数
2.使用双指针,左边的指针i指向最左边,右边的指针j指向最右边,先从右边开始
3.如果右边的数大于基数,右指针j往左移动,如果小于基数就停下来,向右移动左指针i
4.如果左指针的数据小于基数,左指针往右移动,如果大于基数就停下来,然后左指针和有指针的数据交换位置
5.重复 3 和 4,直到 i和j都指向一个位置,第一轮排序完成,后面就对左边和右边重复 步骤 3 和 4直到排序完成
public class QuickSort { public static void sort(List<Integer> list) { if (null == list || list.size() < 2) { return; } sort(list,0,list.size() - 1); } private static void sort(List<Integer> list, int low, int high) { if (low > high) { return; } int i,j,temp,t; i = low; j = high; temp = list.get(low); while (i < j) { // 从右往左,碰到小于基数的停止 while (i < j && temp <= list.get(j)) { j--; } // 从左往右, 碰到大于基数的停止 while (i < j && temp >= list.get(i)) { i++; } if (i < j) { t = list.get(i); list.set(i,list.get(j)); list.set(j,t); } } // 最后将i和j相等的位置与基数互换:i=j,要么i对应的数大于基数,要么小于基数 list.set(low,list.get(i)); list.set(i,temp); // 低柜调用左半数组:j-1 和 j+1 表示i=j的位置就不参与排序了,因为i=j的左边时小于i的,右边时大于j的数,如果这里让i=j参与排序就无法正确排序 sort(list,low,j-1); sort(list,j+1,high); } }
8.堆排序
利用完全二叉树的特性:
若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
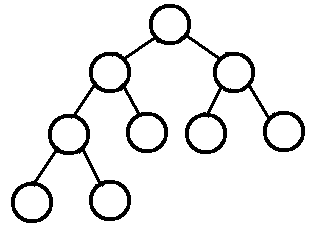
堆是具有以下性质的完全二叉树,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:

同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子:

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤:
1、基本思想
将待排序序列构造成一个大顶堆,此时整个序列的最大值就是堆顶的根节点,将其与末尾元素进行交换,此时末尾为最大值。然后将剩余n-1个元素重新构造成一个堆,堆顶继续为n-1个元素的最大值,然后再将其与倒数第二位的元素交换。如此反复执行,便能得到一个有序序列。
2、算法描述
(1) 构造初始堆,将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
假设给定无序序列结构如下:
4 6 8 5 9
此时我们从最后一个非叶子结点开始,顺序从下至上(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,索引1对应的值是6),从左至右,从下至上进行调整。

找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。

9与4交换之后,该子树[4, 5, 6]为非大顶堆,需要调整为大顶堆,[4, 5 ,6]中6最大,交换4和6。

此时,我们就将一个无需序列构造成了一个大顶堆。每个非叶子节点i 都满足:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
(2) 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与倒数第二元素交换,得到第二大元素。如此反复进行交换、重建、交换。

重新调整剩余n-1个元素的结构,使其继续满足大顶堆排序

再将堆顶元素8与倒数第二元素5进行交换,得到第二大元素8

继续进行调整、交换,如此反复进行,最终使得整个序列有序
再简单总结堆排序的基本思路:
(1) 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
(2) 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
(3) 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
public class HeapSort { public static void sort(List<Integer> list) { if (null == list || list.size() < 2) { return; } // 1.构建大堆顶: i=list.size()/2-1,这里时先构建第一个非叶子节点 for (int i = list.size()/2 - 1; i > 0; i--) { ajustHeap(list,i,list.size()); } // 2.调整 堆结构 交换堆顶元素与末尾元素 } private static void ajustHeap(List<Integer> list, int i, int size) { // 取出第一个元素 Integer temp = list.get(i); for (int j = i*2 + 1; j < size; j = j*2 + 1) { // 从i节点开始算也就是 2i + 1,如果左子节点小于右子节点,j指向右子节点 if (j + 1 < size && list.get(j) < list.get(j+1)) { j++; } // 如果子节点大于父节点: 把子节点赋值给父节点 if (list.get(j) > temp) { list.set(i,list.get(j)); i = j; } else { break; } } list.set(i,temp); } }
9.计数排序
原理:见代码注释部分
缺点:取值范围是[m,n]的正整数
/** * 计数排序原理: * 1.将原数据作为新数组的下角标,新数组的值时原来数据出现的次数 * 2.新数组的长度时 原数组的 最大值-最小值 +1 * 3.原数组是右范围的 [m,n]正整数 * * 步骤:1.新建一个统计数组,长度是原数组元素的最大值-最小值+1,下角标就是原数据-最小值,值是原数据出现的次数 * 2.原数据-最小值作为下角标:每出现一次 + 1 * 3.遍历统计数组:再遍历每个元素,然后一次放入原数组 * @param list * @param min * @param max */ public static void countSort(List<Integer> list,int min,int max) { if (null == list || list.size() < 2) { return; } List<Integer> count = new ArrayList<>(max - min + 1); // 原数据-min 作为下脚标统计出现次数 for (int i = 0; i < list.size(); i++) { Integer data = list.get(i); if (null == data) { continue; } int totalCount = count.get(data-min) == null? 0: count.get(data-min); count.set(data - min, ++totalCount); } for (int i = 0,index=0; i < count.size(); i++) { int item = count.get(i); while (item-- != 0) { list.set(index++,count.get(i) + min); } } }
10.桶排序
原理:工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)
实现暂时有点每搞明白,桶如何划分,数据如何划分,后面再补充






 浙公网安备 33010602011771号
浙公网安备 33010602011771号