四 图卷积的公式推导

1 定义图上的卷积操作

假定有一个函数，输入是图的邻接矩阵，输出是L/Lsym这种性质比较好的矩阵

F（A）可以分解：

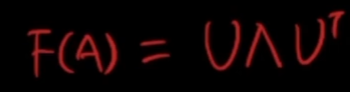
 那么我们定义图上的卷积操作

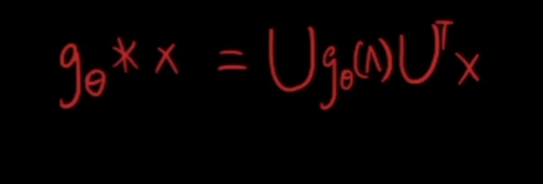
 先让X去新的域，再进行操作，最后用逆变换变回来

作出限制：gΘ（尖）是λ的多项式函数：

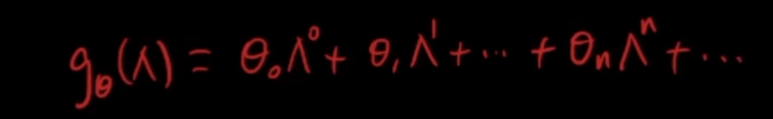
 2 限制的好处

 如果上述函数是多项式函数，那么就需要做特征分解了

 

 3 实际中使用了切比雪夫多项式，使用上述多项式会有梯度消失和爆炸的问题

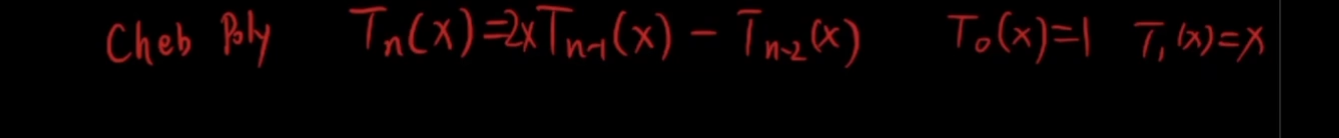
 切比雪夫多项式的优点：

 

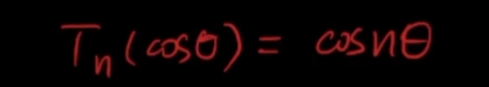
 不管n多大，数值摆动的趋势是稳定的

自变量必须在[-1，1]之间，就是矩阵的特征值再[-1.,1]

上述Lsym的特征值的范围是[1,2]，只要Lsym - E即可满足条件

F（A） = Lsym - E

卷积的定位写作：

 

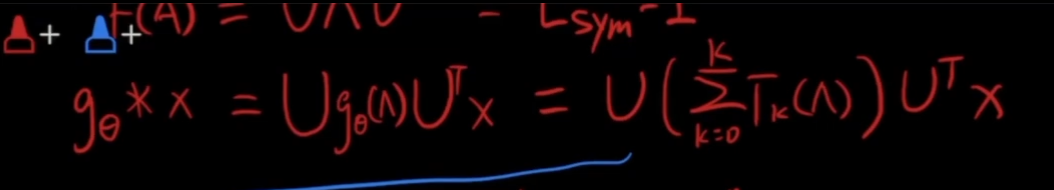
 化解为：

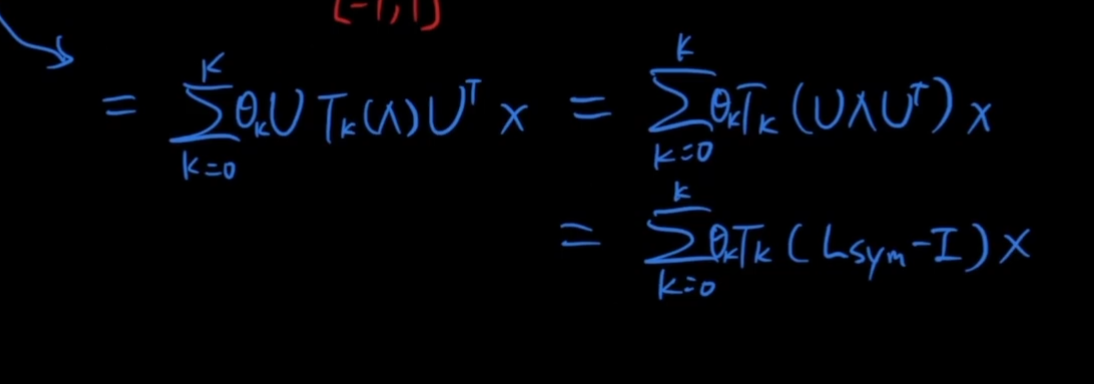
 θ：为学习的系数

以上公式的复杂度依然很高，需要计算K次方，GCN做了一个近似操作,K只要0和1

 

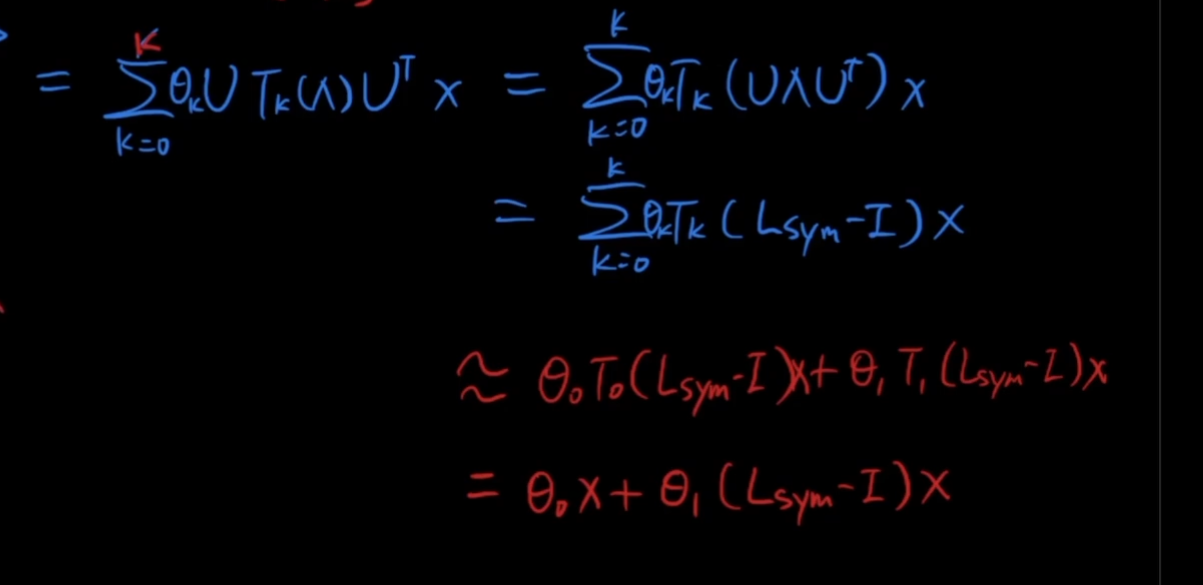
 Lsym的本质是：

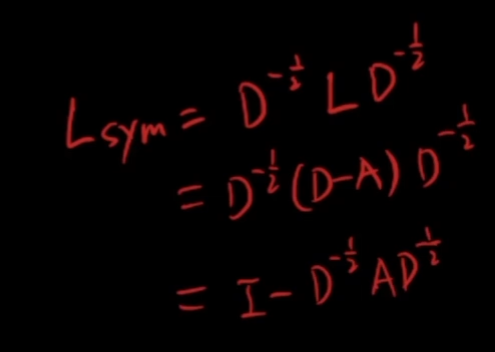
 将上述公式得到的Lsym-I的结果带入展开：

 

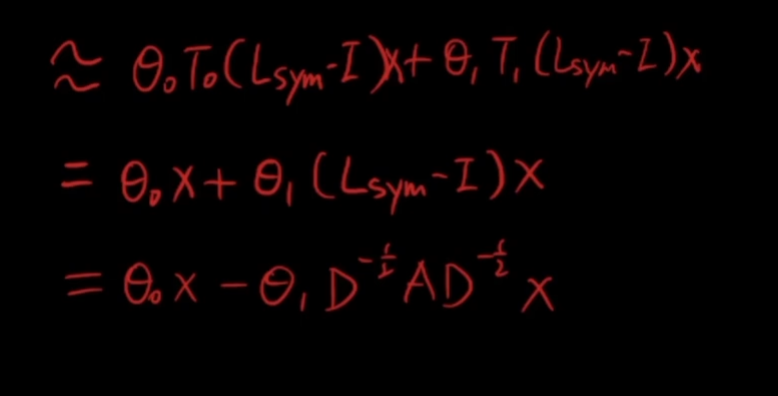
GCN在推导中使用了很多正则化和trick

（1）θ0和θ1共享参数

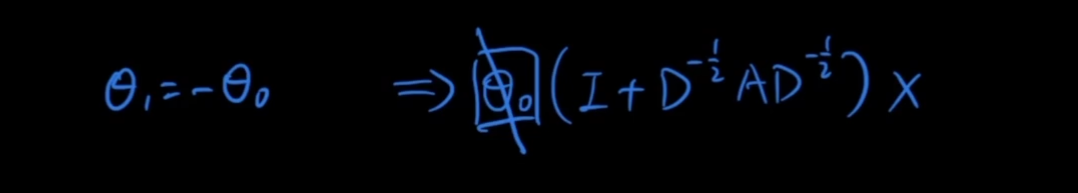
 （2）把I直接加到A中

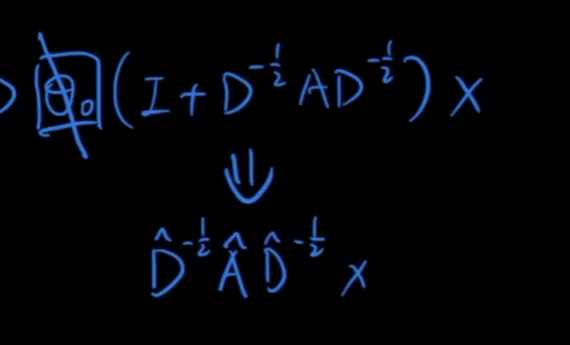
 使用原因是加入trick后效果很好：

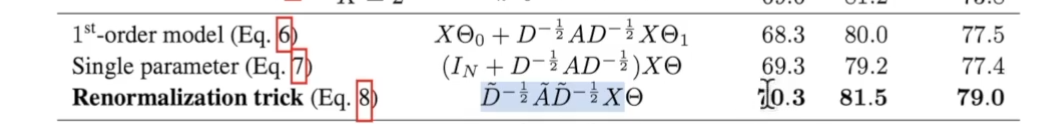
 后续的工作是一阶近似扩展到更高阶的近似方式