1 import matplotlib.pyplot as plt
2 import numpy as np
3 import xlrd
4
5 def sigmoid(x):
6 """
7 Sigmoid function.
8 Input:
9 x:np.array
10 Return:
11 y: the same shape with x
12 """
13 y =1.0 / ( 1 + np.exp(-x))
14 return y
15
16 def newton(X, y):
17 """
18 Input:
19 X: np.array with shape [N, 3]. Input.
20 y: np.array with shape [N, 1]. Label.
21 Return:
22 beta: np.array with shape [1, 3]. Optimal params with newton method
23 """
24 N = X.shape[0]
25 #initialization
26 beta = np.ones((1, 3))
27 #shape [N, 1]
28 z = X.dot(beta.T)
29 #log-likehood
30 old_l = 0
31 new_l = np.sum(-y*z + np.log( 1+np.exp(z) ) )
32 iters = 0
33 while( np.abs(old_l-new_l) > 1e-5):
34 #shape [N, 1]
35 p1 = np.exp(z) / (1 + np.exp(z))
36 #shape [N, N]
37 p = np.diag((p1 * (1-p1)).reshape(N))
38 #shape [1, 3]
39 first_order = -np.sum(X * (y - p1), 0, keepdims=True)
40 #shape [3, 3]
41 second_order = X.T .dot(p).dot(X)
42
43 #update
44 beta -= first_order.dot(np.linalg.inv(second_order))
45 z = X.dot(beta.T)
46 old_l = new_l
47 new_l = np.sum(-y*z + np.log( 1+np.exp(z) ) )
48
49 iters += 1
50 print "iters: ", iters
51 print new_l
52 return beta
53
54 def gradDescent(X, y):
55 """
56 Input:
57 X: np.array with shape [N, 3]. Input.
58 y: np.array with shape [N, 1]. Label.
59 Return:
60 beta: np.array with shape [1, 3]. Optimal params with gradient descent method
61 """
62
63 N = X.shape[0]
64 lr = 0.05
65 #initialization
66 beta = np.ones((1, 3)) * 0.1
67 #shape [N, 1]
68 z = X.dot(beta.T)
69
70 for i in range(150):
71 #shape [N, 1]
72 p1 = np.exp(z) / (1 + np.exp(z))
73 #shape [N, N]
74 p = np.diag((p1 * (1-p1)).reshape(N))
75 #shape [1, 3]
76 first_order = -np.sum(X * (y - p1), 0, keepdims=True)
77
78 #update
79 beta -= first_order * lr
80 z = X.dot(beta.T)
81
82 l = np.sum(-y*z + np.log( 1+np.exp(z) ) )
83 print l
84 return beta
85
86 if __name__=="__main__":
87
88 #read data from xlsx file
89 workbook = xlrd.open_workbook("3.0alpha.xlsx")
90 sheet = workbook.sheet_by_name("Sheet1")
91 X1 = np.array(sheet.row_values(0))
92 X2 = np.array(sheet.row_values(1))
93 #this is the extension of x
94 X3 = np.array(sheet.row_values(2))
95 y = np.array(sheet.row_values(3))
96 X = np.vstack([X1, X2, X3]).T
97 y = y.reshape(-1, 1)
98
99 #plot training data
100 for i in range(X1.shape[0]):
101 if y[i, 0] == 0:
102 plt.plot(X1[i], X2[i], 'r+')
103
104 else:
105 plt.plot(X1[i], X2[i], 'bo')
106
107 #get optimal params beta with newton method
108 beta = newton(X, y)
109 newton_left = -( beta[0, 0]*0.1 + beta[0, 2] ) / beta[0, 1]
110 newton_right = -( beta[0, 0]*0.9 + beta[0, 2] ) / beta[0, 1]
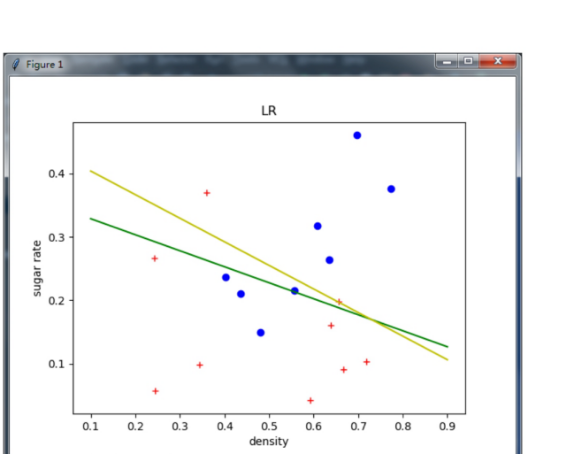
111 plt.plot([0.1, 0.9], [newton_left, newton_right], 'g-')
112
113 #get optimal params beta with gradient descent method
114 beta = gradDescent(X, y)
115 grad_descent_left = -( beta[0, 0]*0.1 + beta[0, 2] ) / beta[0, 1]
116 grad_descent_right = -( beta[0, 0]*0.9 + beta[0, 2] ) / beta[0, 1]
117 plt.plot([0.1, 0.9], [grad_descent_left, grad_descent_right], 'y-')
118
119 plt.xlabel('density')
120 plt.ylabel('sugar rate')
121 plt.title("LR")
122 plt.show()
