统计学习方法 二 感知机

感知机

（一）概念

　　　　　　　　

1，定义：

　　　　　　　　

（二），学习策略

1，线性可分 ：存在一个超平面将正实例和负实例划分开来，反之不可分

2，学习策略：寻找极小损失函数，通过计算误分点到超平面的距离

 　　　　　　　　　　

3，学习算法 即求解损失函数最优化的算法，借用随机梯度下降法

3.1 原始形式  学习率也叫步长（0,1]

　　　　　　　　　　　　

例题：

　　　　　　　　　　　　

　　　　　　　　

　　　　　　　　　　

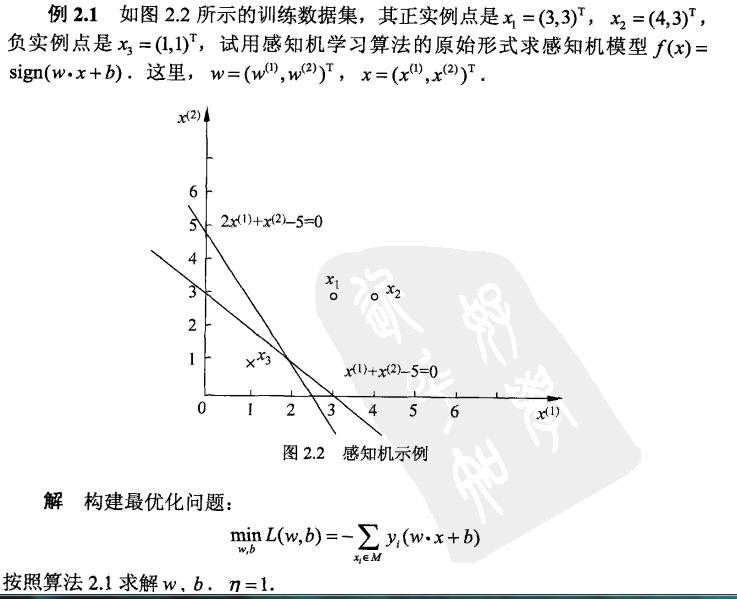
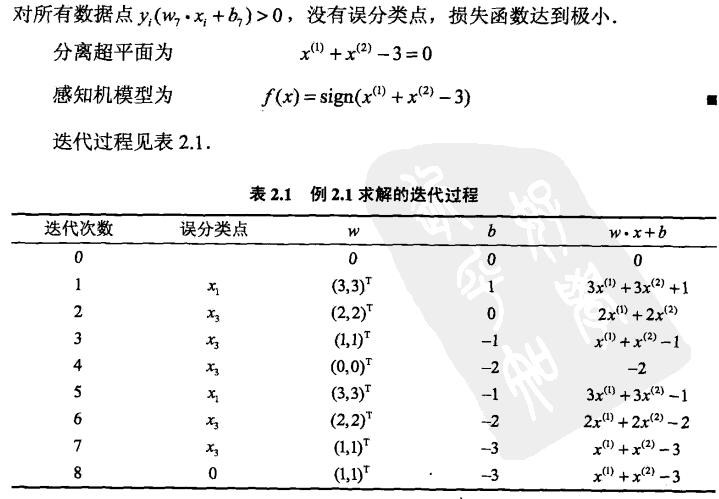
python代码：

#init w,b,
w=[0,0]
b=0
#init datasets
def createDatas():
    return[([3,3],1),([1,1],-1),([4,3],1)]
#updata w and b
def update(item):
    global w,b
    #w+=item[1]*item[0]
    w[0] += item[1] * item[0][0]
    w[1] += item[1] * item[0][1]
    b+=item[1]
    return w,b
#calculate the functional distance between 'item' an the dicision surface. output yi(w*xi+b).
def distance(item):
    dist=0
    for i in range(len(item[0])):
        dist+=w[i]*item[0][i]
    dist+=b
    dist*=item[1]
    return dist
# check if the hyperplane can classify the examples correctly
def check():
    flag=False
    # 计算形式不同：是每次更新w,b，接着就用更新的w,b去跟下个项计算判断
    #还是一直用更新的w,b与原先的项计算判断，哪个快些？，算法思路应该前者，（用if还是while来判断，哪个更快收敛？）
    for item in dataSets:
        if(distance(item=item)<=0):
            flag = True
            update(item=item)
    if not flag:
        print"Result w:",str(w),"b:",str(b)
    return flag
if __name__=="__main__":
    dataSets=createDatas()
    while check():
        pass
#result Result w: [3, 1] b: -5

特点：如果初值不同或步长或选取的误分类点顺序改变，都可能使最后求出的w和b结果不同，针对线性可分的数据

3.2 迭代次数的收敛性：当训练数据集线性可分时，感知机学习算法原始形式迭代是可以收敛

3.3 感知学习机算法对偶形式

          Gram计算：x1*x1,x1*x2,x1*x3 类似

          误分条件：(a1*y1...an*yn)*Gram中每一行 

　　　　　　　　　　　　

　　　　　　　　　　

　　　　　　　　　　

 

 　　　　　　　　　　

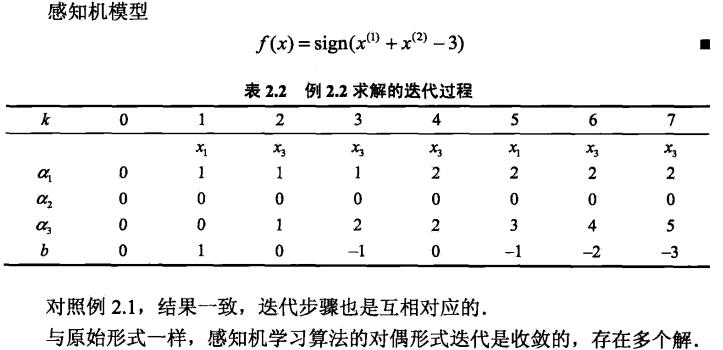
python代码：

import numpy as np
def createDataSets():
    return np.array([[[3,3],1],[[3,4],1],[[1,1],-1]])
#关键理解np.array trainsets[:,1]第二列，trainsets[i][0]指向[3,3],[3,4]这一列，dot内积
def cal_gram():
    g=np.empty((len(trainsets),len(trainsets)),np.int)
    for i in range(len(trainsets)):
        for j in range(len(trainsets)):
            g[i][j]=np.dot(trainsets[i][0],trainsets[j][0])
    return g
def cal(i):
    res=np.dot(alpha*y,Gram[i])
    res=(res+b)*y[i]
    return res
def update(i):
    global alpha,b
    alpha[i]+=1
    b+=y[i]
def check():
    flag=False
    for i in range(len(trainsets)):
        if cal(i)<=0:
            flag=True
            update(i)
    if not flag:
        w=np.dot(alpha*y,x)
        print "Result: w",str(w),"b",b
    return flag
if __name__=="__main__":
    trainsets=createDataSets()
    alpha=np.zeros(len(trainsets),np.float)
    b=0.0
    y=np.array(trainsets[:,1])
    x=np.empty((len(trainsets),2),np.float)
    for i in range(len(trainsets)):
        x[i]=trainsets[i][0]
        Gram=cal_gram()
    while check():
        pass

（四），总结

　　　　　　　　　　

　　　优化方法：但是用普通的基于所有样本的梯度和的均值的批量梯度下降法（BGD）是行不通的，原因在于我们的损失函数里面有限定，只有误分类的M集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降,只能采用随机梯度下降（SGD）或者小批量梯度下降（MBGD）。

　　　对偶使用更多：

　　　　缺陷：泛化能力不强，维度越高，准确率越低，只局限与线性可分的数据集，来寻找最优直线或超平面，但这是支持向量机和神经网络的重要基础，比如支持向量机可以通过核技巧来让数据在高维可分，神经网络可以通过激活函数和增加隐藏层来让数据可分。

　　　　参考目录：

　　　　http://www.cnblogs.com/MrLJC/p/4428443.html

　　　　http://www.cnblogs.com/MrLJC/p/4428443.html