组合数

拓展lucas定理转载自clove大佬

如果你不知道排列组合是什么东西......

排列 A(n,m)＝n(n-1)(n-2)……(n-m+1)＝n!/(n-m)!

组合 C(n,m)=A(n,m)/m!=n!/m!(n-m)!

基本公式

C(n,m)=C(n,n-m)

C(n,m)=C(n-1,m)+C(n-1,m-1)

范德蒙恒等式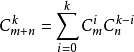

现在开始进入正题

什么？你以为我要讲OI题吗

Too young Too simple!

你还是自己去《五年高考，三年模拟》找几道排列组合题做做吧

组合数1

 t组询问，求C(n,m)%p

 t<=10^5，n,m<=10^6

 p是质数

  预处理出1~n的逆元，直接计算n!*inv[m!]*inv[(n-m)!]

如果你不会求逆元

组合数2

t<=10^5，n,m<=10^3

p不一定是质数

因为p不是质数，所以不能递推求逆元

可以利用公式C(n,m)=C(n-1,m)+C(n-1,m-1)预处理

组合数3

t<=10^5，n,m<=10^18，p<=10^6

p是质数

wow，n,m怎么这么大

这里我们要介绍一个新的定理——lucas定理

假如p为质数，那么：C(n,m)=C(n div p,m div p)*C(n%p,m%p)

直接按照上述规则不断迭代即可

在做组合4之前，推荐你看一下中国剩余定理求模线性方程

 

 

 

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
#define LL long long

LL n,m,MOD,ans;

LL fast_pow(LL a,LL p,LL Mod)
{
    LL ans=1LL;
    for (;p;p>>=1,a=a*a%Mod)
        if (p&1)
            ans=ans*a%Mod;
    return ans;
}
void exgcd(LL a,LL b,LL &x,LL &y)
{
    if (!b) x=1LL,y=0LL;
    else exgcd(b,a%b,y,x),y-=a/b*x;
}
LL inv(LL A,LL Mod)
{
    if (!A) return 0LL;
    LL a=A,b=Mod,x=0LL,y=0LL;
    exgcd(a,b,x,y);
    x=((x%b)+b)%b;
    if (!x) x+=b;
    return x;
}
LL Mul(LL n,LL pi,LL pk)
{
    if (!n) return 1LL;
    LL ans=1LL;
    if (n/pk)
    {
        for (LL i=2;i<=pk;++i)
            if (i%pi) ans=ans*i%pk;
        ans=fast_pow(ans,n/pk,pk);
    }
    for (LL i=2;i<=n%pk;++i)
        if (i%pi) ans=ans*i%pk;
    return ans*Mul(n/pi,pi,pk)%pk;
}
LL C(LL n,LL m,LL Mod,LL pi,LL pk)
{
    if (m>n) return 0LL;
    LL a=Mul(n,pi,pk),b=Mul(m,pi,pk),c=Mul(n-m,pi,pk);
    LL k=0LL,ans;
    for (LL i=n;i;i/=pi) k+=i/pi;
    for (LL i=m;i;i/=pi) k-=i/pi;
    for (LL i=n-m;i;i/=pi) k-=i/pi;
    ans=a*inv(b,pk)%pk*inv(c,pk)%pk*fast_pow(pi,k,pk)%pk;
    return ans*(Mod/pk)%Mod*inv(Mod/pk,pk)%Mod;
}
int main()
{
    scanf("%I64d%I64d%I64d",&n,&m,&MOD);
    for (LL x=MOD,i=2;i<=MOD;++i)
        if (x%i==0)
        {
            LL pk=1LL;
            while (x%i==0) pk*=i,x/=i;
            ans=(ans+C(n,m,MOD,i,pk))%MOD;
        }
    printf("%I64d\n",ans);
}