浅谈向量

本人学艺不精，如有错误，敬请指出……

---

基本知识

定义

指具有大小方向的量，它可以形象化地表示为带箭头的线段。 ——百度百科

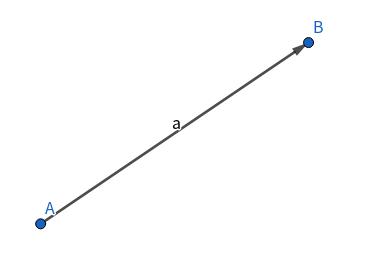
就像上图，就是一个向量的表示形式。

那我们怎么表示一个向量呢？

就是在量上加一个箭头，比如\(\vec{a}\)，在印刷体中也可以记作粗体，比如\(\textbf{a}\)。

当然，在几何中，因为线段是有起点和终点的，我们可以用\(\vec{AB}\)来表示向量。

而向量的坐标表示则如下：

首先先让向量的起点在坐标系的原点，然后设终点的坐标为\(A(a_1,a_2,\cdots,a_n)\)，则向量\(\vec{a}\)用矩阵可以表示为：

\[\vec{a}=\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} \]

相关用法

向量的模

向量\(\vec{a}\)的大小我们用\(|\vec{a}|\)来表示，而向量的大小是一个非负实数。

注意：向量因为带有方向，所以不能比较大小。而向量的模是一个非负实数，所以可一比较大小。

零向量

如果\(|\vec{a}|=0\)，那么我们就把\(\vec{a}\)叫做零向量。

负向量

如果\(|\vec{a}|=|\vec{b}|\)，且\(\vec{a}\)与\(\vec{b}\)的方向相反，那么我们就把\(\vec{b}\)叫做\({\vec{a}}\)的负向量。

相等向量

如果\(|\vec{a}|=|\vec{b}|\)，且\(\vec{a}\)与\(\vec{b}\)方向一样，那么我们把这两个叫做相等向量，可以写作\(\vec{a}=\vec{b}\)。

规定：所有的零向量都相等，

自由向量

如果一个向量起点不固定，那么他可以任意的平行移动。注意不能旋转或翻折，如果旋转或翻折的话方向会改变。

平行四边形法则

设\(\vec{a}=(x_1,y_1)\)，\(\vec{b}=(x_2,y_2)\)。

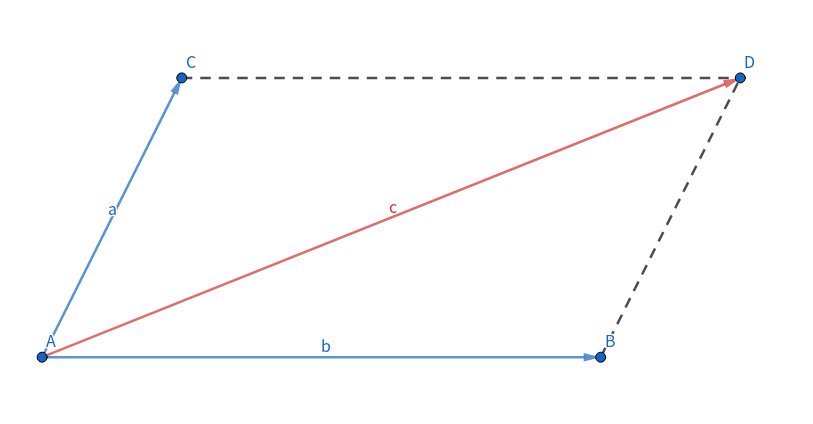
如图，四边形\(ABCD\)为平行四边形，此时\(D(x_1+x_2,y_1+y_2)\)，\(\vec{c}=(x_1+x_2,y_1+y_2)\)，\(\vec{c}=\vec{a}+\vec{b}\)。

这在物理合力的时候会用到。