区块链网络中矿池选择的进化博弈

本文是对《Evolutionary Game for Mining Pool Selection in Blockchain Networks》进行中文翻译、

摘要：

　　在基于工作量证明的区块链网络中，区块矿工参加加密难题解决方案竞赛，以赢得发布（即挖掘）新区块的奖励。 由于加密难题的巨大难度，单个矿工倾向于加入矿池以确保稳定的利润。 我们研究了区块链网络中矿池选择的动力学，其中矿池可以选择任意的区块挖矿策略。 我们将难题解决的哈希率和块传播延迟确定为决定采矿竞争结果的两个主要因素。 然后，我们将个体矿工的策略演变建模为进化博弈。 我们提供了两池案例池选择动力学中进化稳定性的理论分析。 数值模拟支持了我们的理论发现，并证明了一般情况下矿工策略演变的稳定性。

1.介绍

　　一个公共的区块链网络被构建为一个覆盖的点对点（P2P）网络，用于分散的防暴数据记录，可信赖的时间戳或通用的分布式自治组织[1]。 Nakamoto共识协议[2]被用来在经济上激励整个节点（区块矿工）遵守“最长链规则”以维护区块链状态。 遵循该协议，区块挖掘器将任意一组经过验证的交易打包到一个数据结构中，称为候选“区块”，并将其广播到整个网络。 区块链状态被保持为由散列指针[2]以松散同步方式链接的线性块列表。 即，矿工始终保持最长的观察链作为其本地区块链副本。

　　 Nakamoto协议的激励机制包括两个部分[2]：（a）计算密集型密码难题解决过程，使Sybil攻击在经济上难以承受，以及（b）奖励确认过程，以在矿工获得奖励时给予奖励它们发布的块被网络识别。密码难题解决过程被实现为工作量证明（PoW）竞赛[2]，在此过程中，矿工详尽查询可信赖的随机预言，例如SHA-256哈希函数，以找到满足原像的随机字符串根据自己的整体提案的条件。在授予过程中，首先在网络上分发其候选区块的矿工因其在验证新交易中的努力而获得了数字令牌的奖励[1]。与移动网络中普遍的激励机制[3]，[4]相比，Nakamoto协议的特点是在其块确认功能中嵌入了分散式令牌发行方案。每块有固定的奖励，节点加入共识过程的意愿主要受预期的能源消耗成本影响。

　　赢得PoW竞赛的可能性取决于矿工的哈希率（即，矿工每秒对哈希函数的查询次数）与整个网络的总哈希率之间的比率[2]。同时，P2P网络中的区块传播时间决定了一个共识回合内区块确认的最终结果，因为只有传播到大多数节点的第一个区块才被接受为区块链的新头[5]，[6 ]。实际上，由于网络中大量的哈希率，单个矿工赢得PoW竞赛的机会微不足道。结果，现实世界的区块链网络由代表矿工联盟的代理节点所主导，这些矿工被称为矿池[1]。挖掘池通过将前映像搜索任务划分为较小的子任务，然后根据其专门/报告的哈希率将其分配给池中的矿工，从而充当任务调度程序。通过汇总许多矿工的哈希率，采矿池赢得区块奖励的可能性变得非常大。然后，单个矿工可以根据其在池中的哈希率份额来确保获得少量但稳定的回报。

　　在本文中，我们研究了基于PoW的区块链网络中的矿池选择问题。 我们认为个体矿工是有限理性的，矿池采用任意采矿策略[7]。 我们将网络中的池选择动态建模为一个演化游戏。 我们关注哈希率和传播延迟对策略演化的影响，并研究在两个采矿池的情况下池选择动力学的演化稳定性。

2.问题表述

 A.具有工作量证明的财务激励性区块挖掘

　　我们考虑具有N个个体矿工的基于PoW的区块链网络[2]，这些矿工将自己组织到M个矿池中，其集合由M = {1,2，…，M}表示。 我们假设密码难题解决过程是ASIC抵抗[1]。 换句话说，矿工将通用计算单元用于哈希查询，并且具有大致相同的哈希效率，即每瓦特的哈希率。 采矿池i要求每个加入该池的矿工提供一定的哈希率ωi。 令表示哈希率向量。 此外，令表示各个池的人口分数矢量，以使x处于（M-1）-单复数，即 那么，第i池赢得采矿比赛的概率为[1]

 

 　　池i将一个挖出的块广播到对等端，以将其传播到整个网络。 块传播时间由每个链路上的传输延迟和每个中继节点上的事务验证时间确定。 对于大小为s的块，可以将传输延迟建模为，其中γ是与网络规模相关的参数，而c是每个链路的平均有效信道容量[5]。 同时，由于验证交易需要固定的计算量，因此块验证时间可以建模为线性函数，其中β是由网络规模和每个节点的平均验证速度确定的参数 。 然后，大小为s的块在网络上传播的平均时间为

 

 　　由于传播延迟而放弃（即孤立）有效候选块的事件遵循平均速率为1 / T的泊松过程，该过程由网络维持为固定的平均挖掘速率[2]。 因此，孤立一个大小为s的有效块的概率为

 

 然后，池i最终以si的大小块赢得采矿比赛的概率为：

 

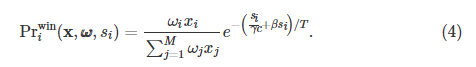
 　　区块奖励包括固定的令牌发行奖励和打包在新区块中的交易费用[1]。 考虑区块链用户为每笔交易支付固定费用，并且交易记录的大小相同。 令R表示发行令牌的奖励，ρ表示每单位数据大小的交易确认价格。 然后，交易费用可以表示为ρsi[6]。 由于哈希计算，矿工还必须考虑能源成本。 令p表示在T期间保持单位哈希率的能源价格。 能量成本可以表示为pωi。 根据（4），矿工在矿池i中的预期收益可以表示为

 

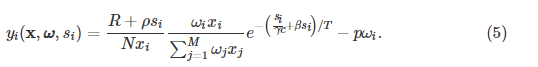
 B.矿池选择作为一种进化游戏

考虑到每个单独的矿工都是有限理性的，其目标是使（5）中给出的收益最大化。 然后，我们可以将用于选择矿池的演化博弈定义为4元组：，其中（a）N是种群 个体矿工的| N | = N，（b）M = {1,2，…，M}是采矿池的集合，（c）x∈X是人口状态的向量，（d）{ yi（x，ωω，si）}i∈M是每个采矿池中单个矿工收益的集合。 我们注意到，ωi和si构成了池i的预定策略。 然后，通过成对比例模仿协议[8]，用于种群进化的复制器动力学可以表示为以下系统的常微分方程（ODE），∀i∈M[8]：

 

 

 其中是池i的大小随时间的增长率，是矿工在该区域的平均收益 池。 令表示所有采矿池的收益向量。 G的纳什均衡（NE）可以定义如下：

定义1（NE[9]）：

如果对所有可行状态的不等式成立，总体状态在游戏G的NE E（Y）集中。

显而易见，NE是（6）中给出的ODE的固定点，即∀i∈M，[8]。 然后，我们需要进一步研究NE状态x ∗∈E（Y）的稳定性，以进行池选择。 假设存在另一种人口状态x'，试图通过吸引矿工人口中的一小部分ϵ∈（0,1）进入x'来入侵状态x ∗。 然后，如果满足所有条件的以下条件，则x ∗是进化稳定策略（ESS）：

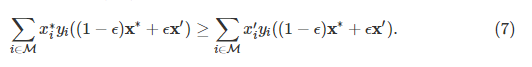
基于（7），我们可以如下正式定义ESS。

定义2（ESS[9]）

 人口状态x ∗是游戏G的ESS，如果存在邻域B∈X，使得∀x∈B−x ∗，则条件（x−x ∗）⊤Y（x ∗）= 0意味着（ x ∗ -x）⊤Y（x）≥0。

我们在算法1中提出了遵循成对比例模仿协议的N个矿工的策略演变[8]。 随着种群的增加，协议代表了（6）描述的复制器动态。

矿池选择的算法1成对比例模仿协议

 

 

 

 C.两个矿池的案例研究

由于空间的限制，我们研究了两个采矿池（M = 2）的情况，以举例说明在池选择游戏中对NE进行稳定性分析的过程。 令每个池的人口分数为x1 = x和x2 = 1-x。 从定义1并通过求解，i∈[1,2]，我们可以得到（6）给出的ODE的三个休止点，形式为（x ∗，1-x ∗） ：

 

 

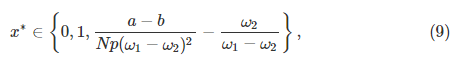
 经过一些数学运算后，我们得到a =（R +ρs1）ω1e−（s1γc+βs1）/ T和b =（R +ρs2）ω2e−（s2γc+βs2）/ T。 值得注意的是，a和b分别代表矿池1和矿池2中单个矿工的预期奖励。 为了满足x在（M-1）-simplex中的条件，我们也有

 

 

 现在，我们准备研究这三个固定点的进化稳定性。 在x ∗ = 0和x ∗ = 1的情况下，总体状态分别为（0，1）和（1，0）。 我们知道这两个固定点具有相似的形式，因为每个采矿池的单独收益函数都相似。 因此，我们只需要检查x1 = x ∗ = 0的情况。

引理1：

对于具有两个挖矿池的游戏G，1）如果x ∗ = 0，则剩余点为ESS，如果

 

 

 2）如果的休止点是ESS

 

 

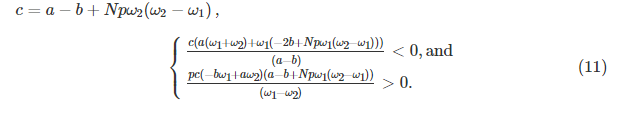
 证明：

通过[8，定义2.6]，可以保证（6）中的ODE的渐近稳定状态是一个ESS。 当复制器动力学是连续时间时，如果平衡时动力学系统的雅可比矩阵是负定的，则它是渐近稳定的[10]。 对于（6）中的ODE，具有两个挖掘池的网络的雅可比矩阵为

 

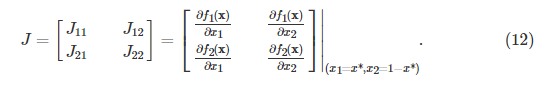
此外，（12）中的元素派生如下：

 

 

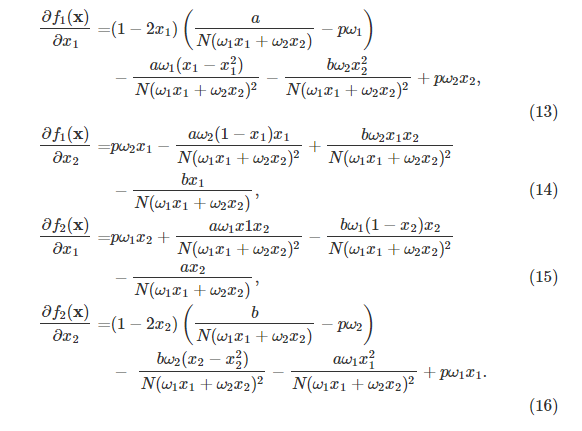
 基于（13）–（16），我们有

1.经过一些标准的数学操作后，如果x * = 0时其主要未成年人的行列式满足以下两个条件，则J为负定额：

 

 

 

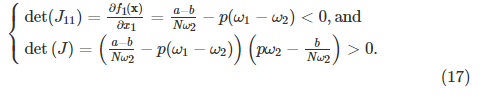
2.相似的，在可以得到以下两个条件，以使J为负定：

 

 

 

 

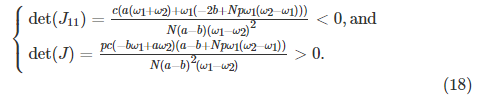
 （17）和（18）中的不等式分别分别是引理1给出的（10）和（11）中的条件。 因此，引理1的证明完成。

在实际情况下，区块链网络由大量矿工组成。 然后，从引理1中，我们可以采用渐近分析，并获得关于其余点的演化稳定性的以下定理。

定理1：

假设人口规模N足够大。 那么，x ∗∈{0,1}的其余点都不是演化稳定的。剩下的点满足以下条件的ESS：

 

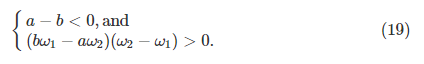
 证明：

在余数1处x ∗ = 0的休止点处，如果ω1≤ω2，则对于雅可比行列式，可以得到limN→+∞det（J11）≥0，则雅可比行列式不是负定的。 或者，如果ω1>ω2，则limN→+∞det（J11）<0和limN→+∞det（J）<0。 同样，雅可比矩阵也不是负定的。 然后，x ∗ = 0的休息点不是ESS。 遵循相同的过程，我们可以证明x ∗ = 1的静止点也不是演化稳定的。

同时，我们知道X内部的任何静止点都是NE [10]。 然后，对于的NE，遵循引理1，我们得到

 

 

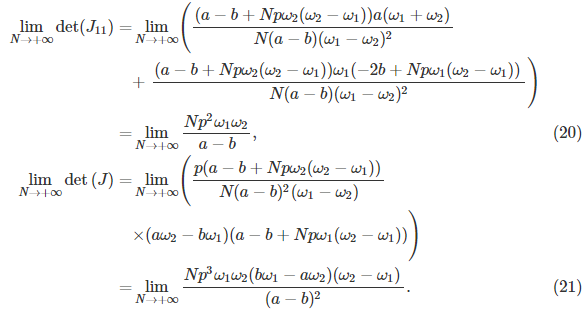
 通过（20）和（21），如果满足（19）中给出的条件，雅可比矩阵为负定。 因此，NE（x ∗，1-x ∗）是ESS。 然后，完成了对定理1的证明。