动态规划——背包问题小结

·好巨的一玩意儿，一口气停下来脑子混的一锅粥（此处一万个艹）

·现在的小可爱在干嘛呢？当然是在山东济南集训的啦~这就为day4宝宝觉得很难的一个小内容~

 

一、小数背包

没展开，目前我也不知道什么东东。

---

 二、完全背包

·特征：n种物品，v容量背包，每件物品有无限次使用权,从前往后.

·状态转移方程式：

（Ps/ C[ ]---物品的费用；W[ ]---物品的价值。）

·边界条件： 

 

f[0][v]=-∞原因：使用前0个物品并且v恰好被用完的价值，为了保证f[v][0]不会作为最优解输出 。

·时间改进：

f[k][v]=max{ f[k-1][v-c[k]*x]+w[k]*x (0<=x<=v/c[k]) }

把上面的v换成v-c[k]得
f[k][v-c[k]]=max{ f[k-1][v-c[k]*(x+1)]+w[k]*x (0<=x<=v/c[k]-1) }

上式令x右移
f[k][v-c[k]]
=max{ f[k-1][v-c[k]*x]+w[k]*(x-1) (1<=x<=v/c[k]) }
=max{ f[k-1][v-c[k]*x]+w[k]*x (1<=x<=v/c[k]) } - w[k]

单独拿出f[k-1][v]得
f[k][v]
=max{ f[k-1][v-c[k]*x]+w[k]*x (0<=x<=v/c[k]) }
=max( f[k-1][v] , max{ f[k-1][v-c[k]*x]+w[k]*x (1<=x<=v/c[k]) } )
=max( f[k-1][v] , f[k][v-c[k]] + w[k] )

·空间改进：

f[k-1]前面的解再也没有用到（昙花一现），故可以只存当前的f[k].

所以去掉数组一维度，即省去k的部分.

·

---

 三、01背包

·特征：n件物品，v容量背包，每一件物品只有唯一使用权，从后往前.

·空间改进：

---

·代码比较：

---

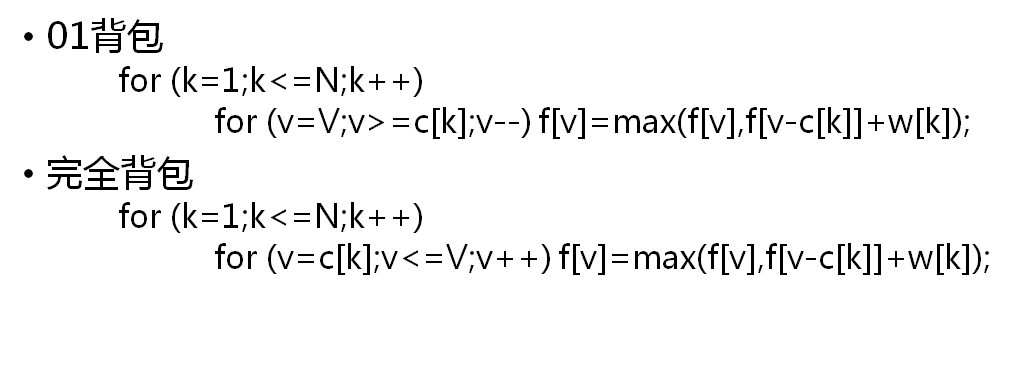
 四、多重背包

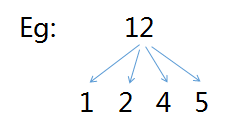
·特征：n种物品，v容量背包，每件物品有对应数量可用.

·思路：

---

五、分组背包

·特征：n件物品，v容量背包，每组中只能选出其中一个物品. 

---

 六、有依赖的背包

---

 

七、混合背包

·示例：一个旅行者有一个最多能装V公斤的背包，现在有n件物品，它们的重量分别是W1，W2，...,Wn，它们的价值分别为C1,C2,...,Cn。 
有的物品只可以取一次（01背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背包）。 
求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。 

#include<iostream>
#include<cstdio>
using namespace std;
int n,v,c[20001],w[20001],p[20001],f[20001];
int main()
{
	cin>>v>>n;
	for(int i=1;i<=n;i++)
	cin>>w[i]>>c[i]>>p[i];
	for(int i=1;i<=n;i++)
	{
		if(p[i]==0)
		{
			for(int j=w[i];j<=v;j++)
			f[j]=max(f[j],f[j-w[i]]+c[i]);//完全背包 
			}
		else
		{
			for(int k=1;k<=p[i];k++)
			for(int j=v;j>=w[i];j--)
			f[j]=max(f[j],f[j-w[i]]+c[i]);//01背包和多重背包 
			}
		}
	cout<<f[v]<<endl;
	return 0;
}

---

八、分层的动态规划

---

九、滚动数组