树状数组

lowbit运算

树状数组，又名二叉索引树，主要用于解决数据变化，其前缀和的变化，它的实现要依赖于lowbit数组，而lowbit函数的建立方法有许许多多种，这边就不一一列举，有兴趣的可以自己百度。这边来列举一个lowbit运算实现操作。

lowbit(44)=lowbit((101100)₂)=(100)₂=4

以这个例子为例，lowbit运算是将一个非负整数n在二进制表示下最低位的1以及其后面的0构成的数值，作为lowbit数值。
因为计算机数据存储用的是补码，且正数的补码和原码相同，负数则为反码+1。

1 0 1 1 0 0(补码) => 44
0 1 0 1 0 0(取反加一) => -44

观察上面的二进制，我们可以发现一个正数的补码和它负数的补码在最低位1之后相同，如果我把它进行与运算时，那么我们是不是可以得到一个二进制数。

0 0 0 1 0 0

它就是我们要的lowbit值，因此我们也可以推到出一个计算lowbit值的公式。

~n+1=-n(~表示取反)
lowbit(n)=n&(~n+1)=n&-n

树状数组

说了这么多，那树状数组到底有什么用，那lowbit运算有什么用。lowbit运算，是将一个数组，转化为一棵二叉树，这也是它名字的由来，如果对二叉树不是很懂的话，建议百度。
由于文字很难说明树状数组的奇妙性，所以我会用图片来表示树状数组的形式。

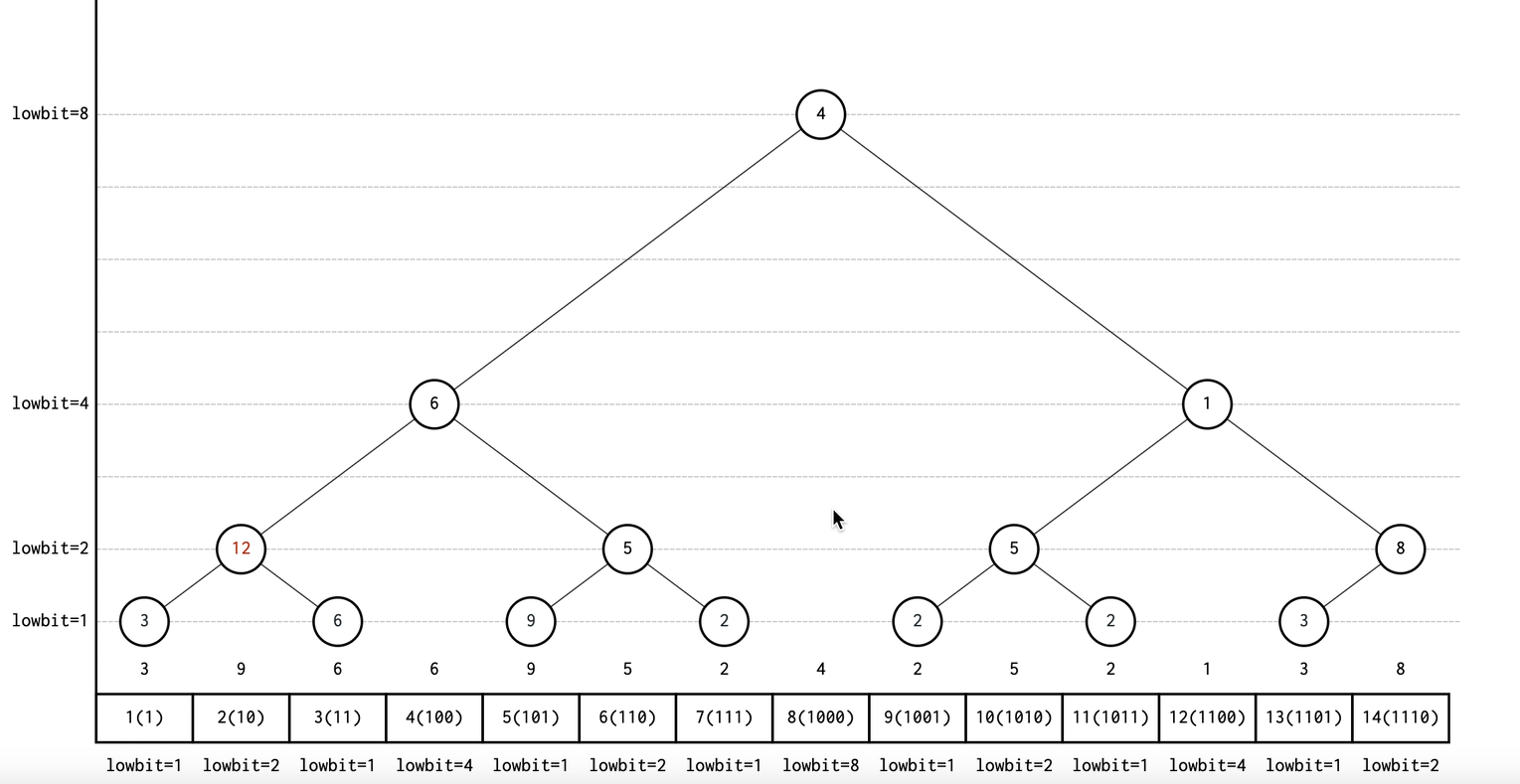
由上面的图片我们可以看到，每个结点值对应数组的值，当我们要查找区间的和时，它的时间复杂度为O(n)。
但是，当我们将这数组转化为树状数组时，如下图

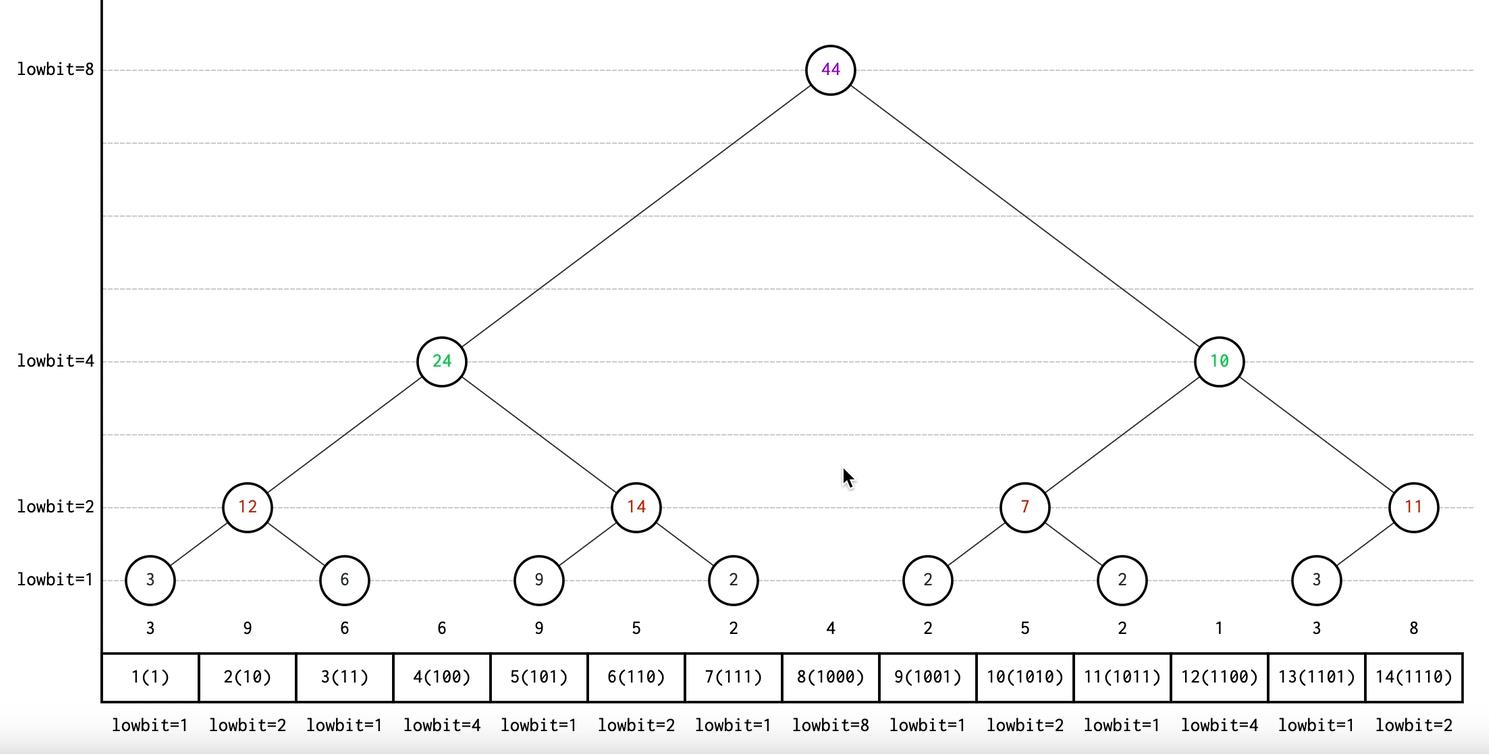
可以看到，根据lowbit值，将相同的lowbit值分层，同时一个数组也转化为树形结构，可以说lowbit值的引入，使得数组可以像二叉树一样。
如果在仔细一点，我们就可以发现它的规律，lowbit不等于1的结点的数值等于左孩子结点值、左孩子的右孩子值（右孩子不为空）和本身结点之和，这就是前缀和了。
而对树状数组进行区间和查询时，它的时间复杂度降为O(log₂n)。

树状数组分析

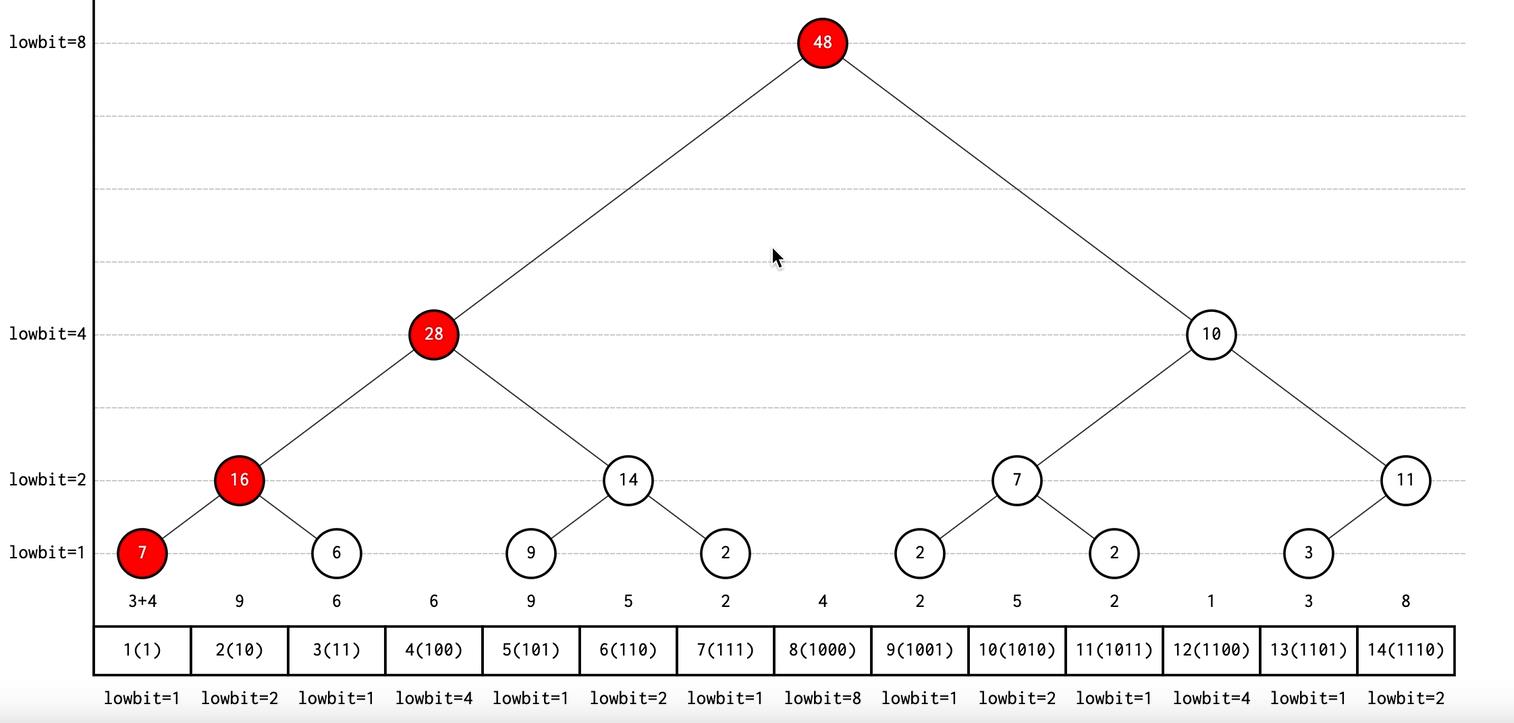
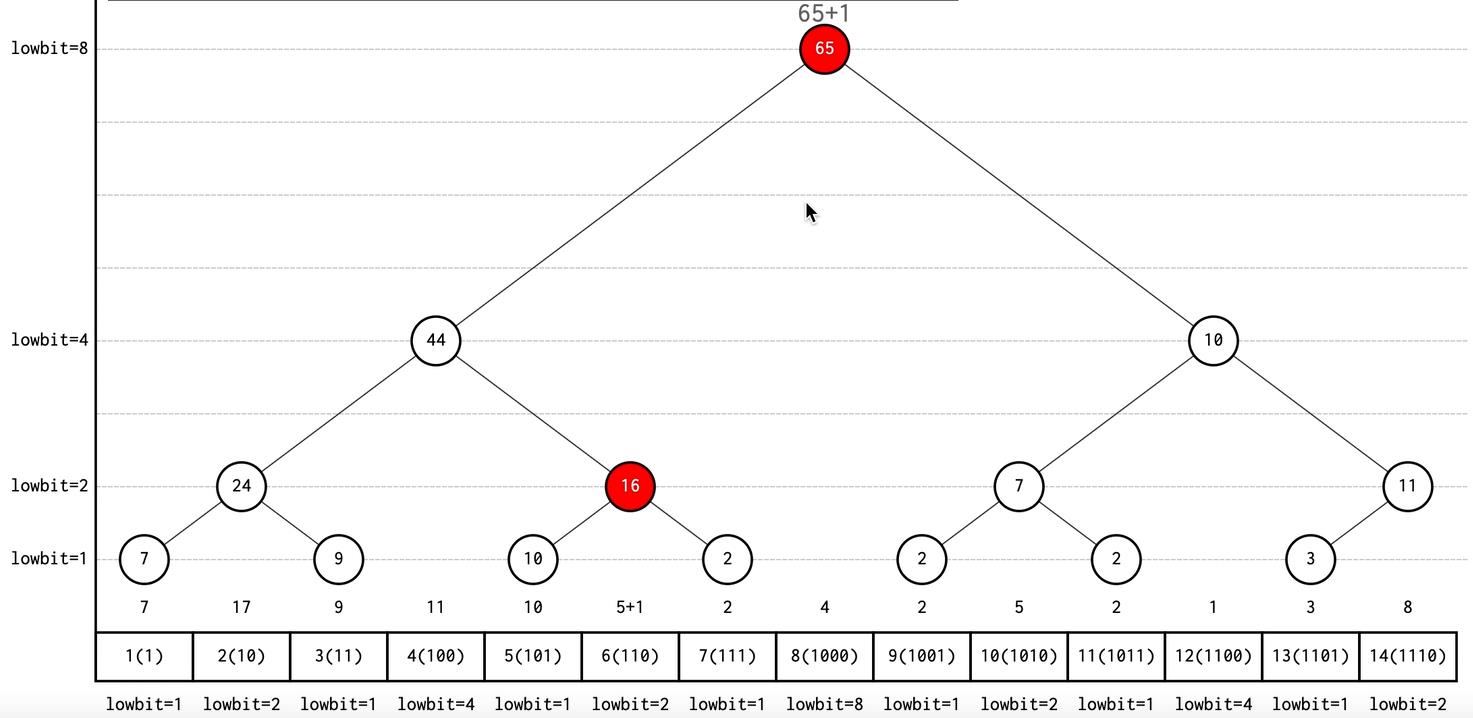
如果我们修改树状数组的值，那么比它后的结点的数值也会发生改变，那么我们应该如何改变他们的值呢，既然我们是通过lowbit的值来创建树状数组，相应的，我们也可以通过lowbit的值来改变整个数组。
像上面两张图一样，我左孩子1结点加一后，数值下标加上lowbit后去变化其他结点的值，同样的，我改变右孩子6结点值，数组下标加上lowbit值就可以改变其他结点的值。
即改变某个结点，改变之后，就要加上该结点的lowbit值去改变相应相应结点的值。

代码实现

//单点修改
//添加函数，x为变化结点，k为增加数值，该结点变化，同时其他对于结点变化
void add(int x,int k)
{
	for(;x<=n;x+=x&-x) t[x]+=k;
}
//前缀和
int ask(int x)
{
	int sum=0;
	for(;x;x-=x&-x) sum+=t[x];
	return sum;
}

修改和查询

单点修改： add(x，k)
单点查询： ask(x)-ask(x-1)
区间查询： ask(r)-ask(l-1)

总结

树状数组能解决的问题其实很少，局限性大，仅仅只是作用于前缀和的计算而已，这就不得不提及另一个数据结构，线段树，它能做树状数组可以解决的事情，但是代码长，编写难度大。