第七章 离散傅里叶变换
离散时间傅里叶变换(DTFT),频域分布是连续频率变量\(w\)的函数,周期为\(2\pi\)。
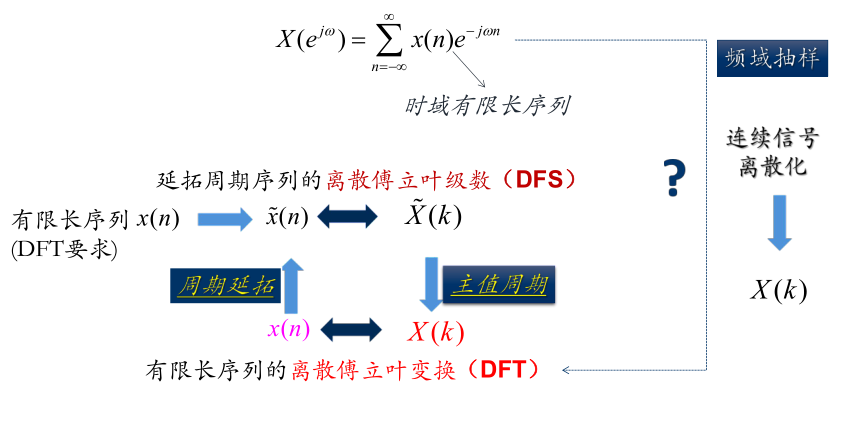
离散傅里叶变换(DFT)是研究时域有限长离散序列与频域有限长离散序列之间所对应的分析工具。
将时域N个独立值变换为频域N个独立值
离散傅里叶变换
思路:周期延拓,借助离散周期信号的离散时间傅里叶级数(DFS)表示DFT(取DFS的主值周期



离散傅里叶变换性质
线性性质
不多bb
圆周移位
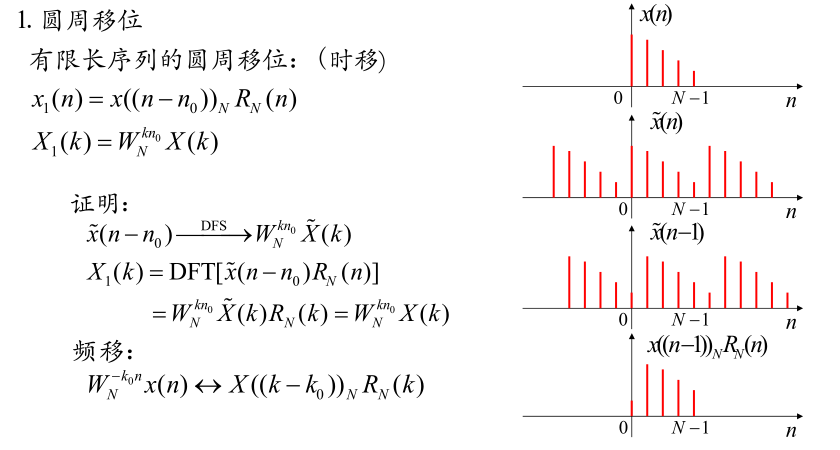
说的很玄乎,其实就是周期性吧
周期卷积与圆周卷积
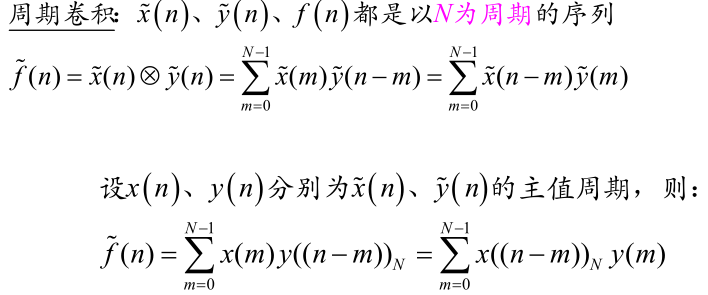

也是进行周期延拓计算后取主值周期
时域与频域卷积
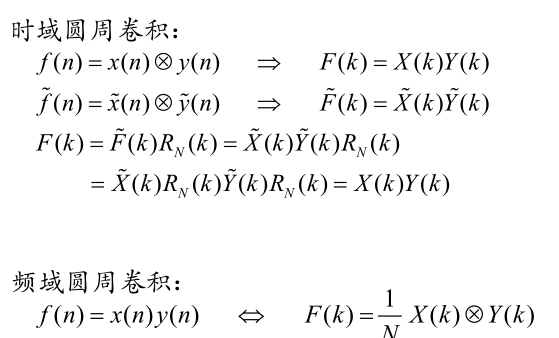
有限长序列线性卷积和圆周卷积

如何计算
?补零!


共轭对称性
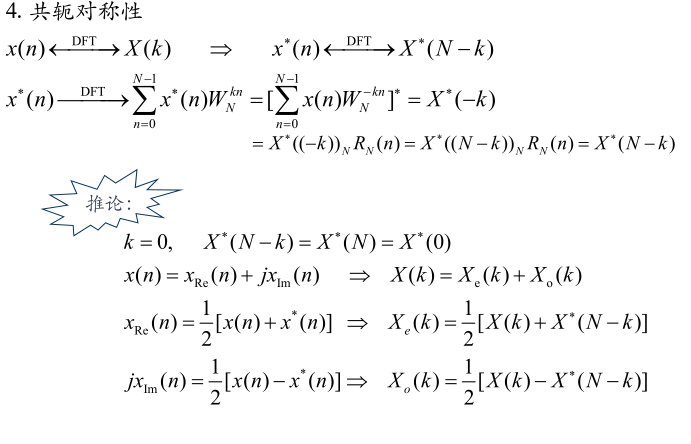

结论:有限长序列的实部对应于\(X(k)\)的圆周共轭偶部,虚部对应于\((k)\)的圆周共轭奇部
帕斯瓦尔定理
快速傅里叶变换(FFT)
DFT运算特点
N点有限长序列一个点计算需要N次复数乘法和N-1次复数加法,计算N个点要\(N^2次复数乘和N(N-1)次复数加\)
- DFT运算特点

思想:
将长序列DFT逐步分解成短序列的DFT,再利用这些性质进行某些组合,来减少运算量

按时间抽取的FFT算法
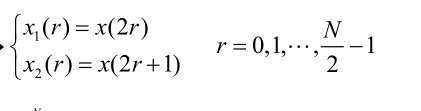
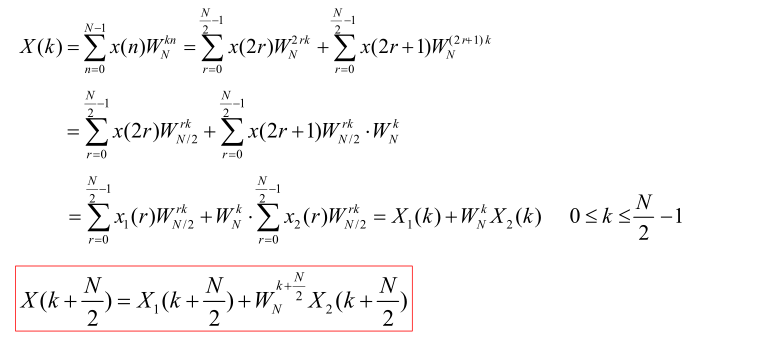
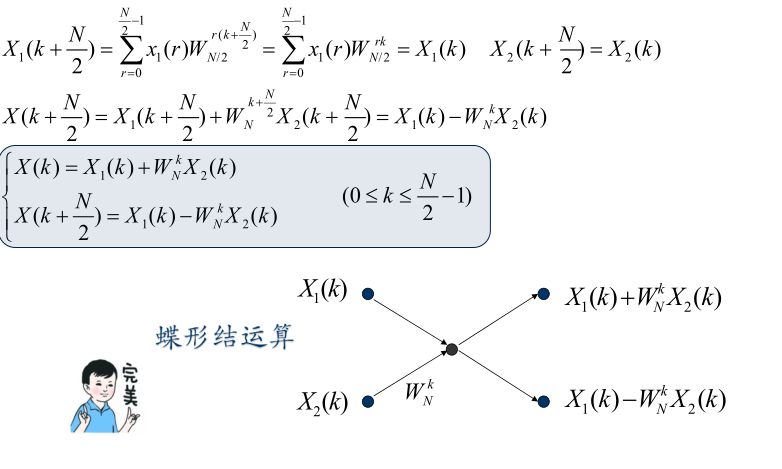

- 图示运算过程
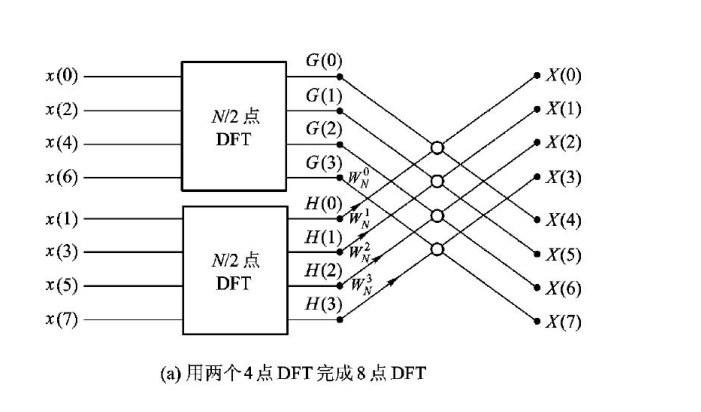
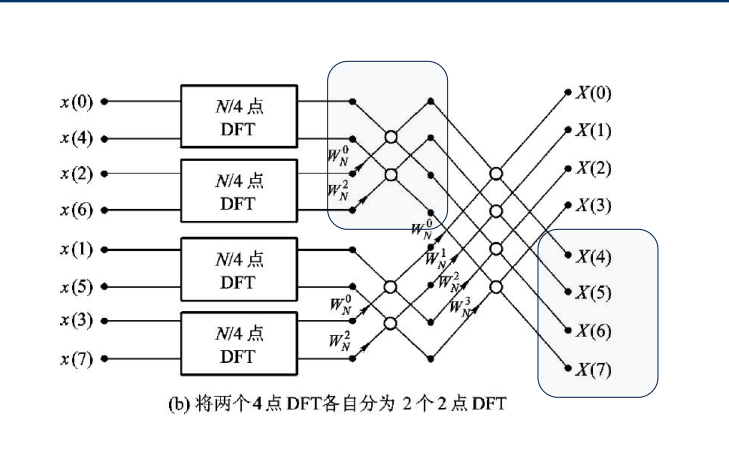
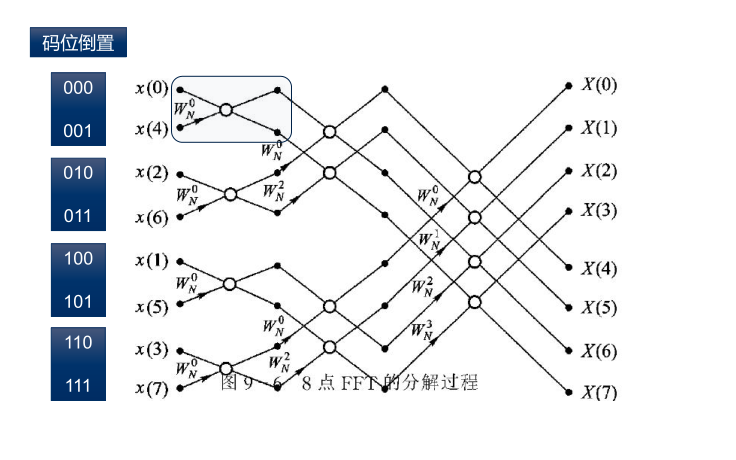
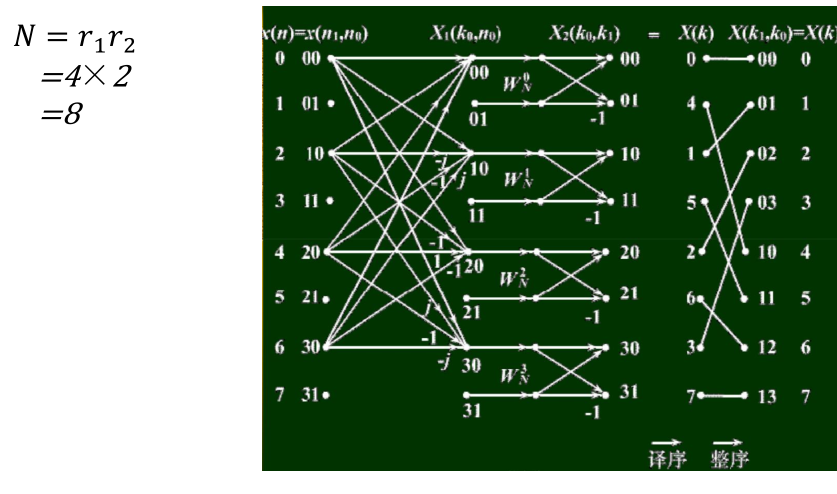
复合数(码位倒置)(这部分蛮晦涩,多做题理解一下)



- 举个栗子--图解更清晰

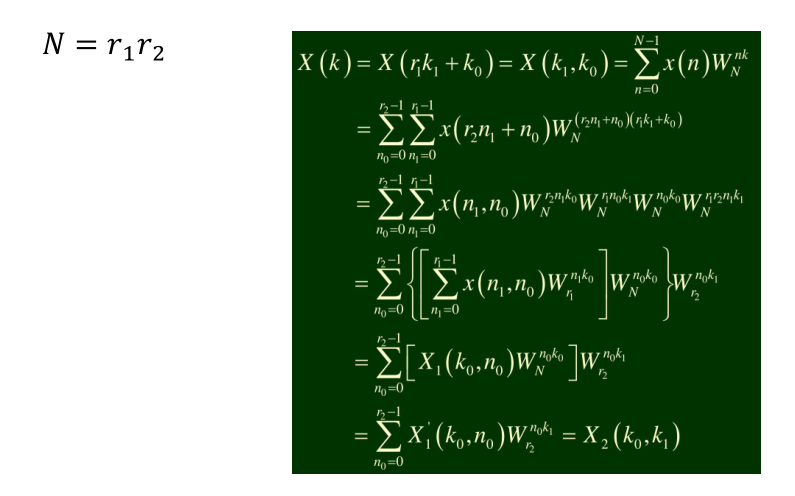




 浙公网安备 33010602011771号
浙公网安备 33010602011771号