分治思想解决算法问题
逆序对

思路一:两层for循环
不多bb,\(O(N^2)\)
- 代码实现
#include <iostream>
using namespace std;
void solve()
{
int a[5000]={0};
int f[5000]={0};
int m;
cin >> m;
for (int i = 0; i < m; i++)
cin >> a[i];
f[0] = 0;
for (int i = 1; i < m; i++)
{
int sum = 0;
for (int j = 0; j < i; j++) {
if (a[j] > a[i]) sum++;
}
f[i] = f[i - 1] + sum;
}
cout << f[m - 1] << endl;
}
int main() {
int m;
cin >> m;
for (int i = 0; i < m; i++)
{
solve();
}
return 0;
}
思路二:分治思想,借助归并排序
- 分治思想:将一组数分为两个部分,所有的逆序对主要有三个来源:
1.左半区间的逆序对
2.右半区间的逆序对
3.右半区间比左半区间大的一对数构成的逆序对
归并排序回顾
- 三个步骤:
-
分解:\(待排序的区间为 [l, r],令 m =\lfloor \frac{l + r}{2} \rfloor 我们把 [l, r] 分成 [l, m]和 [m + 1, r]\)
-
解决:用递归排序递归地排序两个子序列
-
合并:把两个子序列进行合并
-
在待排序序列长度为 1 的时候,递归开始「回升」,因为我们默认长度为 1 的序列是排好序的。
- 思路

rPtr指针所指向的数对逆序对贡献为rPtr
\(O(nlog_n)\) - 代码实现
#include <iostream>
using namespace std;
int mergeSort(int *nums, int *tmp, int l, int r) {
if (l >= r) {
return 0;
}//左指针超出右指针,循环结束
int mid = (l + r) / 2;
int inv_count = 0;
inv_count+=mergeSort(nums, tmp, l, mid) + mergeSort(nums, tmp, mid + 1, r);//递归循环
int i = l, j = mid + 1, pos = l;//i,j为左右指针,pos为临时数组tmp的指针
while (i <= mid && j <= r) {
if (nums[i] <= nums[j]) {//左半区间数比右半区间数小,就把l指针左移,并把数放入tmp数组
tmp[pos] = nums[i];
++i;
inv_count += (j - (mid + 1));//每当左半区间归并入tmp时,就要计算右半区间数对逆序对的贡献
}
else {
tmp[pos] = nums[j];
++j;
}
++pos;
}
for (int k = i; k <= mid; ++k) {
tmp[pos++] = nums[k];
inv_count += (j - (mid + 1));//while循环结束后,左半区间还有剩余情况
}
for (int k = j; k <= r; ++k) {//右半区间还有剩余
tmp[pos++] = nums[k];
}
for(int i=l;i<=r;i++){
nums[i]=tmp[i];
}
//copy(tmp.begin() + l, tmp.begin() + r + 1, nums.begin() + l);//这里是把排序好的tmp数组复制给nums
return inv_count;
}
void solve()
{
int n;
cin>>n;
int *a=new int [n];
int *sum=new int [n];
int i;
for( i=0;i<n;i++)
{
cin>>a[i];
}
cout << mergeSort(a,sum,0,n-1) << endl;
}
int main() {
int m;
cin >> m;
for (int i = 0; i < m; i++)
{
solve();
}
return 0;
}
思路三:树状数组
-
树状数组是一种动态维护数组前缀和的数据结构,功能有
- 单点更新
update(i, v): 把序列 ii 位置的数加上一个值 v,这题 v = 1 - 区间查询
query(i): 查询序列 [1 \(\cdots\) i] 区间的区间和,即 i 位置的前缀和
两个操作都是\(O(log_n)\)
- 单点更新
-
思路

1.求逆序对数量,我们只要求每个数后面有多少个数比这个数小,采用树状数组解决
2.将每个数离散化,用二分查找找到每个数对应的离散后的值
3,求解时,从后往前枚举,先统计后面有多少个数比这个数小,然后在把它加到树中 -
代码实现(用vector比较好写,这里就不写了)
最大子数组和

思路一:两层for循环
不赘述
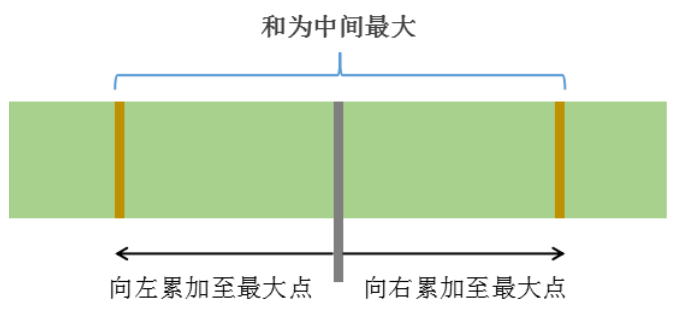
思路二:分治法



 浙公网安备 33010602011771号
浙公网安备 33010602011771号