概率论与随机过程学习笔记 一

随机向量与概率分布

二维随机向量联合分布

二维随机向量联合分布函数

• \(\Omega={\omega}是随机实验E的样本空间，X{\omega},Y{\omega}是两个随机变量,(X,Y)称为E的一个二维随机向量。\)
• \(F(x,y)=P(X\le x,Y\le y)称为(X,Y)的联合分布函数\)
• \(P(x_1< X\le x_2,y_1<Y \le y_2)=F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)\)
  
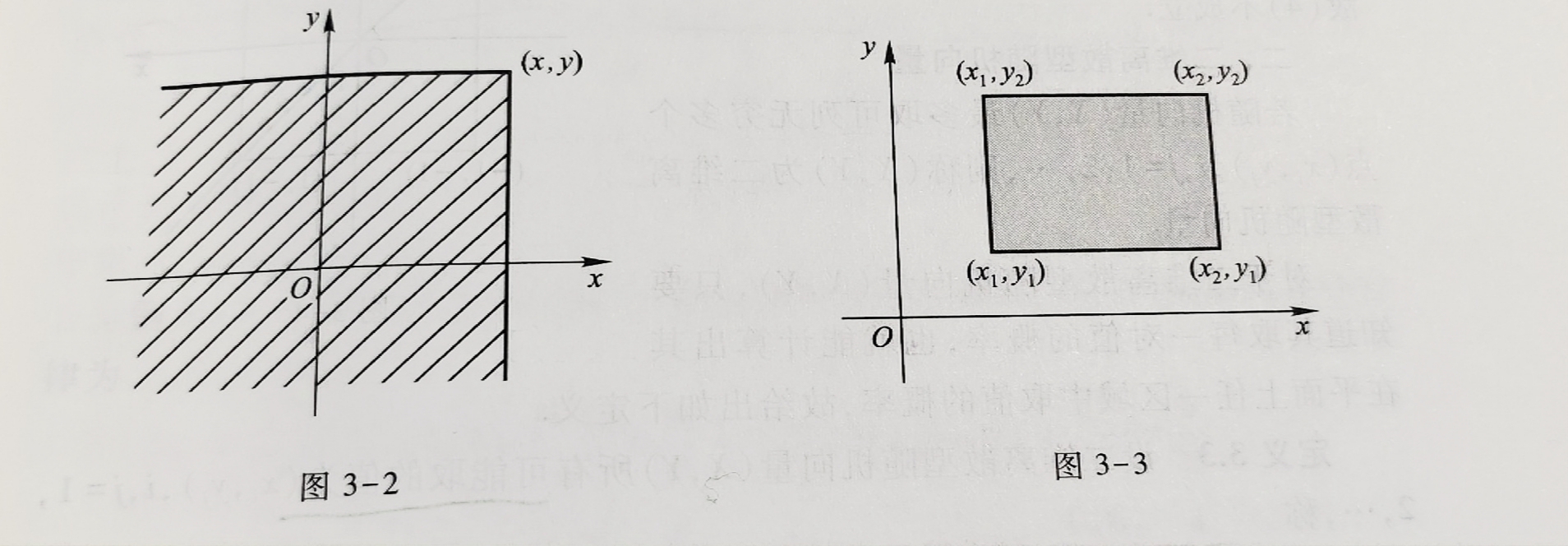
  *\(0\le F(x,y)\le 1\)
  \(F(x,y)关于x,y不降 ，且右连续\)
  \(F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)\ge 0\)

二维离散型随机向量

• $P(X=x_i,Y=y_i)=p_{ij} $
• 可以用表格表示分布律

二维连续型随机向量

• \(F(x,y)=\int_{-\infty}^{y}\int_{-\infty}^xf(x,y)\mathrm{d}x\mathrm{d}y, -\infty\le x,y\le +\infty\)
• \(f(x,y)\)称为(X,Y)的联合概率密度函数
• \(f(x,y) \ge 0\)
  \(\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}x\mathrm{d}y=1\)
  \(若f(x,y)在(x，y)处连续，f(x,y)=\frac{\partial^2F(x,y)}{\partial x\partial y}\)
  \(设G是xy平面上的区域，点(X,Y)落在G内的概率为 P((X,Y)\in G)=\iint_Gf(x,y)\mathrm{d}x\mathrm{d}y\)
• 二维均匀分布
  二维正态分布

边缘分布

边缘分布函数

• \(F_1(x)=F(x,+\infty),F_2(y)=F(+\infty,y) 分别称为(X,Y)关于X和关于Y的边缘分布函数\)
• 边缘分布函数实际上就等于一维变量的分布函数

边缘分布律

• \(P(X=x_i,Y=y_j)=p_{ij}\)
  \(记p_{~i. }=\sum_{j=1}^{\infty}p_{ij}=P(X=x_i)\)

  $p_{.j }=\sum_{i=1}^{\infty}p_{ij}=P(X=y_j) $
  称为边缘分布律