自动控制原理学习笔记 一 连续控制系统分析与设计

连续控制系统分析与设计

线性定常系统，常用的分析方法有：

• 时域分析法
• 根轨迹分析法
• 频率响应分析法

系统响应性能指标与输入信号

• 瞬态响应
  一般用初始条件为零的情况下对单位阶跃输入信号的响应来衡量
• 稳态响应
  t->\(\infty\),系统输出状态

瞬态响应指标：

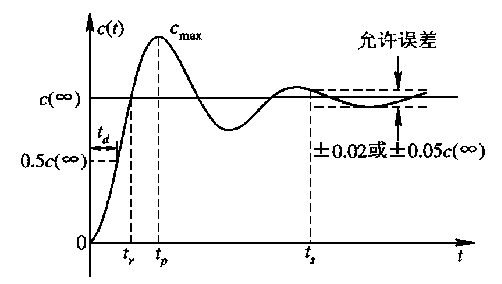
• 超调量 \(\delta\)%
• 延迟时间 \(t_d\)
• 上升时间 &t_r$
• 峰值时间 \(t_p\)
• 调节时间 \(t_s\)
• 稳态误差 \(e_{ss}\)
• 震荡次数 N

典型输入信号：

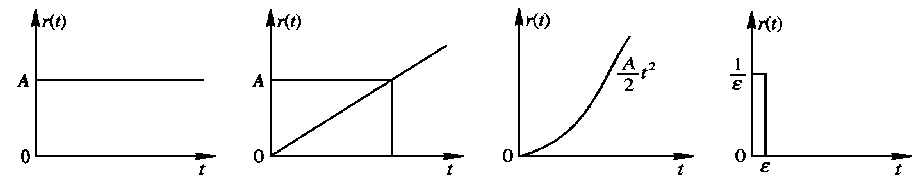
• 阶跃信号
• 斜坡信号
• 抛物线信号
• 脉冲信号

连续控制系统时域分析法：

系统的阶跃响应分析：

一阶系统的阶跃响应

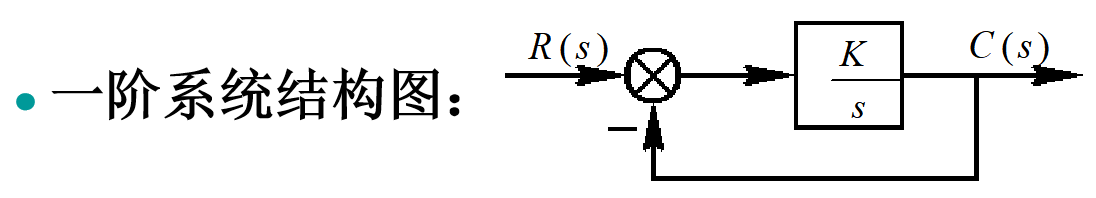
闭环传递函数：\(\Phi(s)\)=\(\frac{C(s)}{R(s)}\)=\(\frac{1}{\frac1ks+1}\)=\(\frac{1}{Ts+1}\) 其中，T为时间常数
单位阶跃输入的拉式变换为：R\((s)\)=\(\frac1s\)
故\(C(s)=\Phi(s) \cdot R(s)=\frac1{Ts+1}\cdot\frac1s\)
取\(C(s)\)的拉氏反变换，可得单位阶跃响应
\(c(t)=L^{-1}[C(s)]\)=\(L^{-1}[\frac1{Ts+1} \cdot \frac1s]\) =\(L^{-1}[\frac1s - \frac1{s+ \frac1T}]\)
故\(c(t)=1-e^{-\frac1Tt}\)
最终稳态： \(c(\infty)=\lim\limits_{x\rightarrow\infty}c(t) =1\)
稳态误差： \(e_{ss}=1 -c（\infty)=0\)

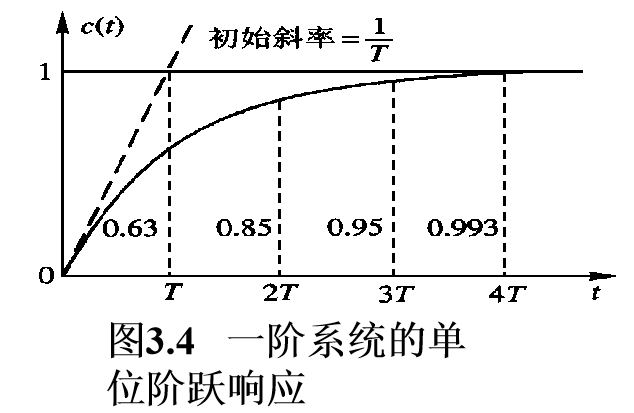
调节时间\(t_s\) 为3T

二阶系统单位阶跃响应

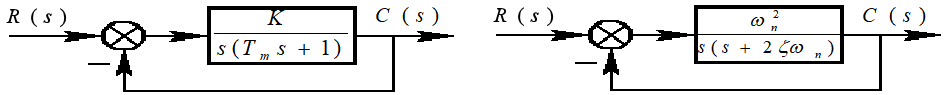
闭环传递函数：： \(\Phi(s)=\frac{C(s)}{R(s)}=\frac K{T_m s^2+s+K}\)
标准形式： \(\Phi(s)=\frac{\omega_n^2}{s^2+2 \zeta \omega_ns+\omega_n^2}\)
典型形式 \(\Phi(s)=\frac{1}{T^2s^2+2 \zeta Ts+1}\)
式中，\(T=\frac1{\omega_n}=\sqrt{\frac K{T_m}}\) \(~~~\) \(\zeta=\frac1{2\sqrt{KT_m}}\)
系统的闭环特征方程为： \(s^2+2\zeta \omega_ns+ \omega^2=0\)
特征根为（系统闭环极点） \(s_{1,2}=-\zeta \omega_n+\omega_n\sqrt{\zeta^2-1}\)
阻尼比不同，特征根性质不同，系统的响应特性也就不同

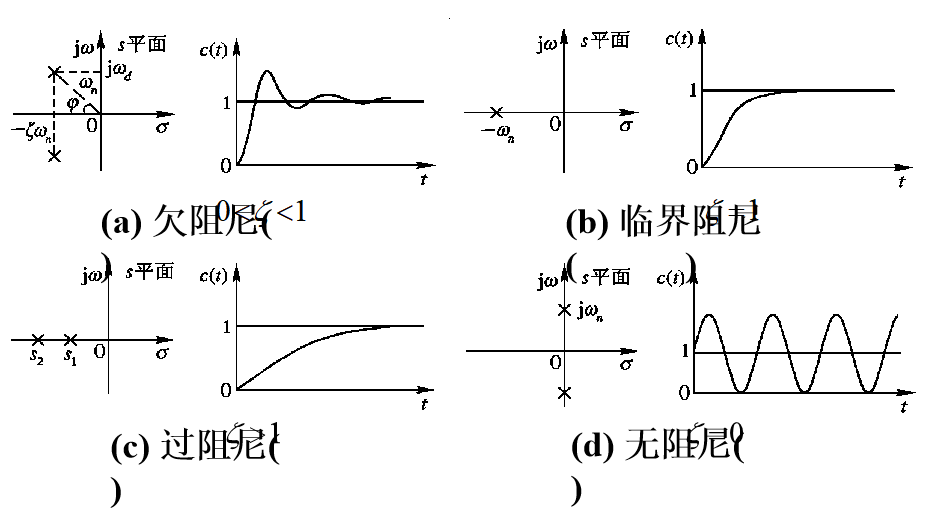
二阶系统的响应性能指标

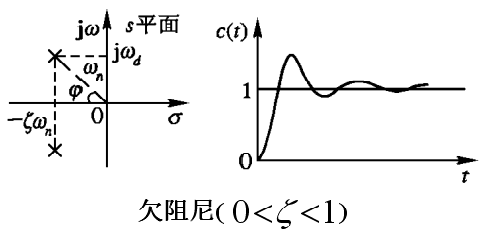
工程实际中常把二阶系统调整为欠阻尼系统；

• 上升时间\(t_r=\frac{\pi-\theta}{\omega_d} ~~ tan(\theta)=\frac{\sqrt{1- \zeta^2}}{\zeta} ~~\omega_d=\omega_n \sqrt{1-\zeta^2}\) \(~~~~~~~~~~\)

• 峰值时间\(t_p=\frac{\pi}{\omega_d}\)

• 超调量\(\delta\)% (懒得打了）

• 调节时间\(t_s\)

• 稳态精度 \(t\rightarrow \infty\) ，稳态误差\(e_{ss}=0\)

控制系统稳定性

当系统的所有输入信号为零时，在非零初始条件下，如果系统的输出信号随时间的推移而趋于0，则称系统是稳定的。

线性定常系统稳定的充分必要条件

• 线性定常系统的微分方程的一般形式：
  \(a_n\frac{d^n}{dt^n}c(t)+a_{n-1}frac{d^{n-1}}{dt^{n-1}}c(t)+\cdots+a_1\frac{d}{dt}c(t)+a_0c(t) =b_m\frac{d^m}{dt^m}r(t)+b_{m-1}\frac{d^{m-1}}{dt^{m-1}}+\cdots+b_1\frac{d}{dt}r(t)+b_0r(t)\)

• 考虑初始条件取上式拉氏变换
  \(C(s)=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{a_ns^n++a_{n-1}s^{n-1}+\cdots+a_1s+a_0}R(s) +\frac1{a_ns^n++a_{n-1}s^{n-1}+\cdots+a_1s+a_0}N_0(s)\)
  \(N_0\)为非0初始信号

• 根据稳定性定义，r(t)=0时系统响应
  \(C_0(s)=\frac1{a_ns^n++a_{n-1}s^{n-1}+\cdots+a_1s+a_0}N_0(s)\)
  

• 线性定常系统稳定的充分必要条件： 系统的闭环极点（特征根）全部具有负实部。即所有极点分布在s平面的左半部。

劳斯稳定判据：

• 必要条件：控制系统的特征方程的所有系数均为正值，且特征方程不缺项。
• 劳斯表：
  
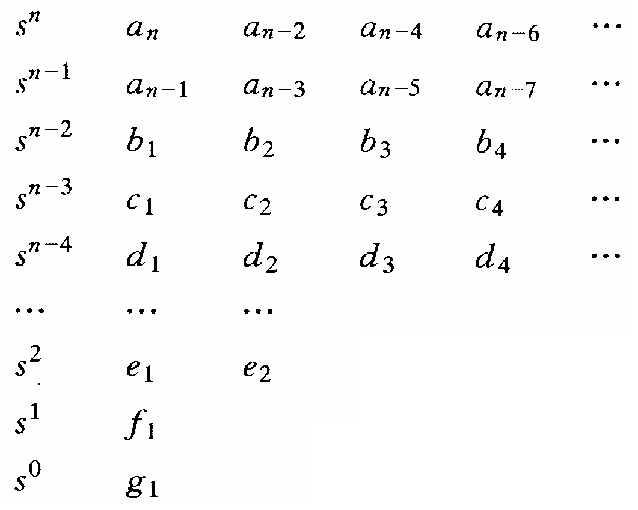
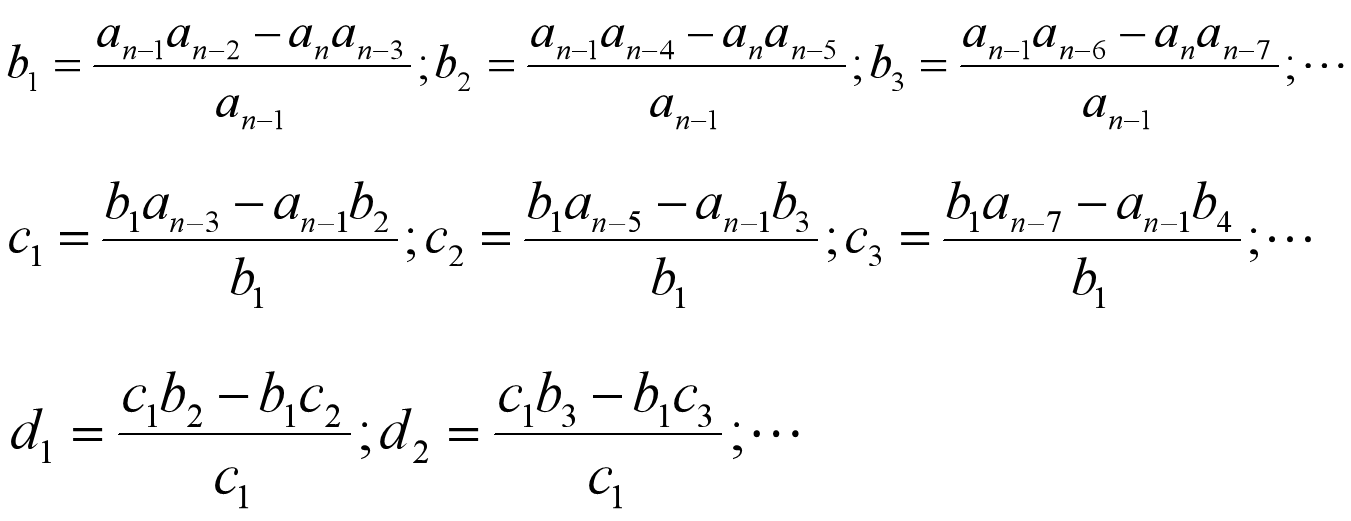
• 劳斯稳定判据是劳斯表的第一列各项元素均为正数

反馈控制系统的稳态误差

• 稳态误差是对系统精度的一种衡量，它表示系统实际输出值与希望输出值之间的最终误差
• 稳态误差的概念
  
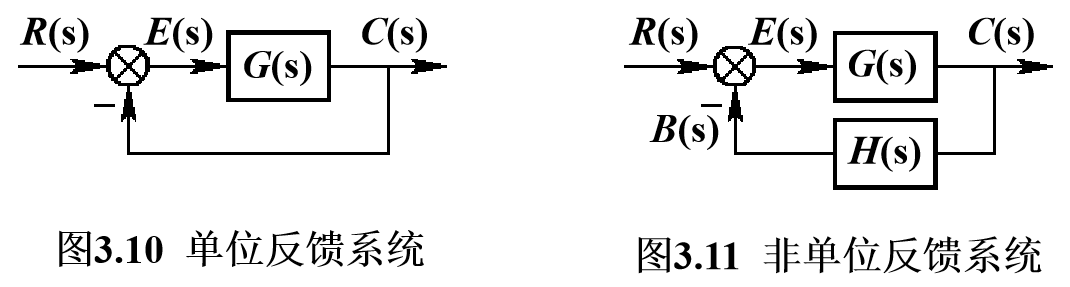
• \(e_{ss}=e(\infty)=\lim\limits_{t\rightarrow\infty}e(t)=\lim\limits_{t\rightarrow\infty}[r(t)-b(t)](对于单位反馈系统，c(t)=b(t))\)
• 误差信号e(t)与输入信号r(t)之间的传递函数为
  \(\Phi(s)=\frac{E(s)}{R(s)}=\frac1{1+G(s)H(s)}\)
• 根据终值定理，稳定系统稳态误差为
  \(e_{ss}=\lim\limits_{t\rightarrow\infty}e(t)=\lim\limits_{t\rightarrow\infty}sE(s)=\lim\limits_{s\rightarrow 0}\frac{sR(s)}{1+G(s)H(s)}\)

稳态误差的计算

• 稳态误差可分为由给定信号引起的误差和由扰动信号引起的误差
  

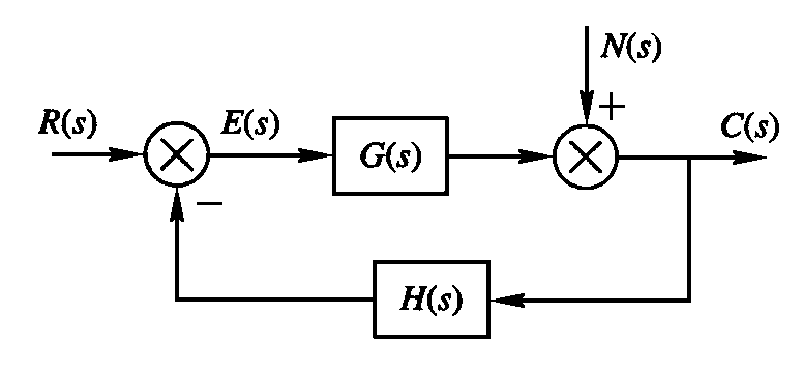
给定信号作用下的稳态误差及误差系数

• 扰动信号D(s)=0;
• \(e_{ss}=\lim\limits_{t\rightarrow\infty}e(t)=\lim\limits_{t\rightarrow\infty}sE(s)=\lim\limits_{s\rightarrow 0}\frac{sR(s)}{1+G(s)H(s)}\)
• 系统输入的一般表达式为：
  \(R(S)=\frac{A}{s^N}~~~\) N为输入信号的阶次
• 系统开环传递函数的一般表达式
  \(G(s)H(s)=\frac{K\prod_{j=1}^m(\tau_j s+1)}{s^v\prod^{n-v}_{i=1}(\Tau_is+1)}\triangleq \frac{K}{s^v} \cdot G_0(s),n \ge m\)
  \(s^v表示系统在原点处有v重极点，也就是包含v个串联积分环节,称为v型系统\)
  \(系统的稳态误差与v，K有关\)

单位阶跃输入的稳态误差

• $R(s)=\frac1s $
• 稳态误差 $e_ss= \lim\limits_{s\rightarrow 0}\frac{s}{1+G(s)H(s)}\cdot\frac1s=\frac1{1+G(0)H(0)}=\frac1{1+K_p} $
• \(K_p=G(0)H(0),称为静态位置误差参数\)
• \(对于0型系统： K_p=K ,此时稳态误差 e_{ss}=\frac1{1+K}\)
• \(对于v（v\ge1） 型系统，K_p=\infty ,e_{ss}=0.\)
• 若要求系统对阶跃输入稳态误差为0 ，则系统型号至少为1 ，即前向通道中必须有积分环节

单位斜坡输入

单位抛物线输入

总结

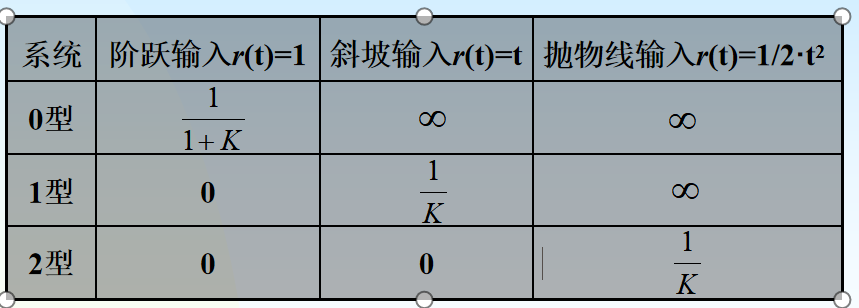
• K为系统的开环增益

扰动信号引起的稳态误差

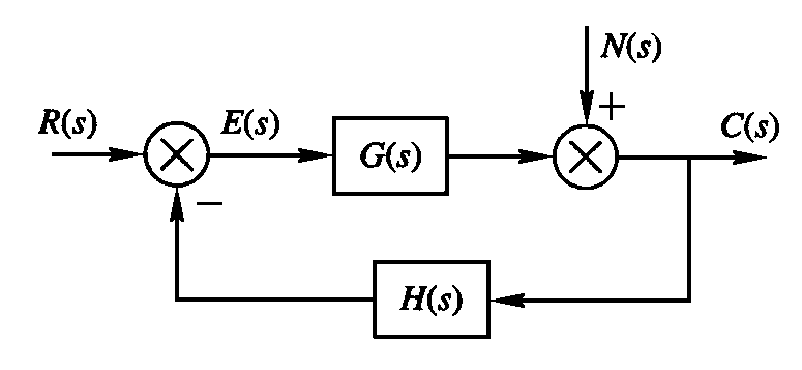
• 主要扰动为N(s)
• 系统输出 \(C(s)=\Phi_n(s)N(s)=\frac1{1+G(s)H(s)}\cdot N(s)\)
• 误差与输出和扰动之间的关系
  \(E(s)=-H(s)C(s)=-\frac{H(s)}{1+G(s)H(s)} \cdot N(s)\)
• 稳态误差
  \(e_{ss}=\lim\limits_{s\rightarrow 0}sE(s)=\lim\limits_{s\rightarrow 0}\frac{-H(s)}{1+G(s)H(s)} \cdot sN(s)\)
• 若扰动为单位阶跃信号， 即n(0)=1 ,且G(0)H(0)>>1
  \(e_{ss}=\frac{-H(0)}{1+G(0)H(0)}\approx -\frac1{G(0)}\)

降低稳态误差

1）增大系统开环放大系数可以增强系统对参考输入的跟随能力；增大扰动作用点以前的前向通道放大系数可以降低扰动引起的稳态误差
2）增加前向通道中积分环节数，使系统型号提高，可以消除不同输入信号时的稳态误差。

• 增加前向通道中积分环节数，或增大系统开环放大系数，都使闭环传递函数的极点发生变化，从而降低系统的稳定性，甚至造成系统不稳定。
  3）采用复合控制系统，对误差信号进行补偿，提高稳态精度，也称为前馈控制。

按扰动信号复合的控制系统

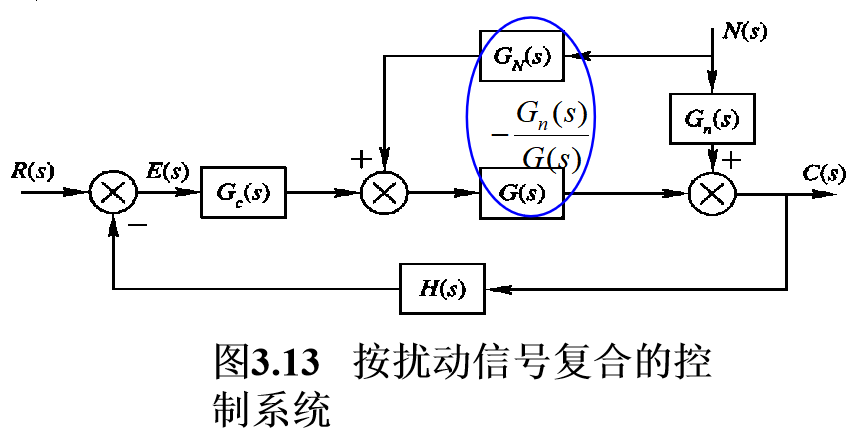
频域分析法

奈奎斯特判据

• 预备知识：映射定理
  \(设F(s)为两个s的多项式之比，在s平面上一封闭曲线内F(s)的极点数为P，零点数为Z。当变量s顺时针通过封闭曲线时，相应的轨迹顺时针包围F(S)的原点总次数等于Z-P\)

奈奎斯特稳定性判据（充要条件）

若系统开环传递函数在s右半平面内无任何极点，则为保证系统稳定性，\(G(s)H(s)\)(开环幅相频率特性曲线）的轨迹必须不包围\(-1+0j\)点

相角裕度与幅值裕度（了解）

开环频率特性与系统稳态性能的关系