常见数据挖掘算法的Map-Reduce策略(2)
接着上一篇文章常见算法的mapreduce案例(1)继续挖坑,本文涉及到算法的基本原理,文中会大概讲讲,但具体有关公式的推导还请大家去查阅相关的文献文章。下面涉及到的数据挖掘算法会有:Logistict 回归,SVM算法,关联规则apriori算法,SlopeOne推荐算法,二度人脉社交推荐算法
logistict regression的map-reduce
逻辑回归作为经典的分类算法,工业界也是应用的非常广泛(点击率预估,广告投放等),貌似大部分互联网公司都会用吧,关于logistict regression的应用研究主要分两块:1)用什么样的正则(L2,L1); 2)使用什么优化算法;关于第一点,如果维度超级多选L1较好,L1天然具有特征选择的优势,另外常用的优化算法有:梯度下降,LBFGS、随机梯度下降,以及微软针对L1提出的OWLQN算法;原本的logisitc回归,是针对线性可分的的,业界的一淘企业的工程师扩展了Logistic回归,用它来处理非线性的问题。
针对多种优化算法,梯度下降,LBFGS,OWLQN都是可以无损的并行化(执行结果与串行的一样),而基于随机梯度下降的只能进行有损的并行化。
以梯度下降为例:梯度下降的核心步骤![]() ,每一次迭代的个过程可以转换成一个map-reduce过程,按行或者按列拆分数据,分配到N各节点上,每个节点再通过计算,最后,输出到reduce,进行合并更新W权重系数,完成一次迭代过程。下图文献1中也提到LR的并行,不过用的优化方法是
,每一次迭代的个过程可以转换成一个map-reduce过程,按行或者按列拆分数据,分配到N各节点上,每个节点再通过计算,最后,输出到reduce,进行合并更新W权重系数,完成一次迭代过程。下图文献1中也提到LR的并行,不过用的优化方法是
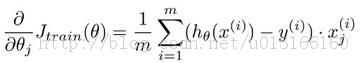 ,每一次迭代的个过程可以转换成一个map-reduce过程,按行或者按列拆分数据,分配到N各节点上,每个节点再通过计算,最后,输出到reduce,进行合并更新W权重系数,完成一次迭代过程。下图文献1中也提到LR的并行,不过用的优化方法是
,每一次迭代的个过程可以转换成一个map-reduce过程,按行或者按列拆分数据,分配到N各节点上,每个节点再通过计算,最后,输出到reduce,进行合并更新W权重系数,完成一次迭代过程。下图文献1中也提到LR的并行,不过用的优化方法是Newton-Raphson,节点需要计算海森矩阵。

针对随机梯度的并行,下图文献2中提到


算法1是基本的SGD算法,算法2,3是并行的SGD, 可以看出每台worker分配T个数据,利用这些数据来SGD优化更新W,然后输出W由reduce端进行归约。
SVM的map-reduce
支持向量机,最近十五年机器学习界的明星算法,学术界也是各种研究,现今已经达到一个瓶颈,屋漏偏逢连夜雨,随着深度学习的雄起,SVM弄的一个人走茶凉的境遇(也许正是90年代神经网络的感受吧,呵呵),现在讲一讲关于SVM的并行,由于原算法较难应用并行策略,而它的另一个算法变种-pegasos 适合并行,下面是该算法的过程。
初始化W=0(向量形式)
for i in t:
随机选择K个样本
for j in K:
if 第j个样本分错
利用该样本更新权重
累加W的更新
end for
下面是基于mrjob的map-reduce版
1 class MRsvm(MRJob): 2 3 DEFAULT_INPUT_PROTOCOL = 'json_value' 4 5 #一些参数的设置 6 7 def __init__(self, *args, **kwargs): 8 9 super(MRsvm, self).__init__(*args, **kwargs) 10 11 self.data = pickle.load(open('data_path')) 12 13 self.w = 0 14 15 self.eta = 0.69 #学习率 16 17 self.dataList = [] #用于收集样本的列表 18 19 self.k = self.options.batchsize 20 21 self.numMappers = 1 22 23 self.t = 1 # 迭代次数 24 25 26 def map(self, mapperId, inVals): 27 28 #<key,value> 对应着 <机器mapperID,W值或者样本特征跟标签> 29 30 if False: yield 31 32 #判断value是属于W还是样本ID 33 34 if inVals[0]=='w': 35 36 self.w = inVals[1] 37 38 elif inVals[0]=='x': 39 40 self.dataList.append(inVals[1]) 41 42 elif inVals[0]=='t': self.t = inVals[1] 43 44 45 def map_fin(self): 46 47 labels = self.data[:,-1]; X=self.data[:,0:-1]#解析样本数据 48 49 if self.w == 0: self.w = [0.001]*shape(X)[1] #初始化W 50 51 for index in self.dataList: 52 53 p = mat(self.w)*X[index,:].T #分类该样本 54 55 if labels[index]*p < 1.0: 56 57 yield (1, ['u', index])#这是错分样本id,记录该样本的id 58 59 yield (1, ['w', self.w]) #map输出该worker的w 60 61 yield (1, ['t', self.t]) 62 63 64 def reduce(self, _, packedVals): 65 66 for valArr in packedVals: #解析数据,错分样本ID,W,迭代次数 67 68 if valArr[0]=='u': self.dataList.append(valArr[1]) 69 70 elif valArr[0]=='w': self.w = valArr[1] 71 72 elif valArr[0]=='t': self.t = valArr[1] 73 74 labels = self.data[:,-1]; X=self.data[:,0:-1] 75 76 wMat = mat(self.w); wDelta = mat(zeros(len(self.w))) 77 78 for index in self.dataList: 79 80 wDelta += float(labels[index])*X[index,:] #更新W 81 82 eta = 1.0/(2.0*self.t) #更新学习速率 83 84 #累加对W的更新 85 86 wMat = (1.0 - 1.0/self.t)*wMat + (eta/self.k)*wDelta 87 88 for mapperNum in range(1,self.numMappers+1): 89 90 yield (mapperNum, ['w', wMat.tolist()[0] ]) 91 92 if self.t < self.options.iterations: 93 94 yield (mapperNum, ['t', self.t+1]) 95 96 for j in range(self.k/self.numMappers): 97 98 yield (mapperNum, ['x', random.randint(shape(self.data)[0]) ]) 99 100 101 def steps(self): 102 103 return ([self.mr(mapper=self.map, reducer=self.reduce, 104 105 mapper_final=self.map_fin)]*self.options.iterations)
关联规则Apriori的map-reduce
啤酒跟尿布的传奇案例,相信大家都应该非常熟悉了,但是很悲剧的是这个案例貌似是假的,呵呵,超市的管理者一般会把这两个放在相差很远的位置上摆放,拉长顾客光顾时间,或许就不止买尿布跟啤酒了。前段时间看到一个东北笑话也许会更容易理解关联规则,“一天,一只小鸡问小猪说:主人去哪了? 小猪回答说:去买蘑菇去了;小鸡听完后,立马撒腿就跑了,小猪说你走这么急干啥,小鸡回头说:主人如果买粉条回来,你也照样急。。。。”很形象生动的讲述了关联规则,好了,又扯远了了,现在回到关联规则的并行上来吧,下面以一个例子简述并行的过程。
假设有一下4条数据
id,交易记录
1,[A,B]
2,[A,B,C]
3,[A,D]
4,[B,D]
首先,把数据按行拆分,搞到每个worker上面,key=交易id,value=交易记录(假设1,2在第一个mapper上,3,4在第二个mapper上)
其次,每个worker,计算频次(第一个mapper生成<A,1>,<B,1>,<A,1>,<B,1>,<C,1> ;第二个mapper 就会生成<A,1>,<D,1>,<B,1>,<D,1>)
接着,进行combine操作(减轻reduce的压力)(第一个mapper生成<A,2>,<B,2>,<C,1> ;第二个mapper 就会生成<A,1>,<B,1>,<D,2>)
最后,送到reduce上面进行归约,得到1-频繁项集
然后再重复上面的动作,知道K-频繁项集
总结:这是对Apriori的并行实现,但是该算法的一个缺点是需要多次扫描数据,性能是个问题,对此,韩教授设计了另外一个更巧妙的数据结构fp-tree,这个在mahout里面是有实现的(0.9的版本里面貌似把这算法给kill了。。),总体来说关联规则这个算法是一个听起来是一个很实用的算法,实际操作过程中要仔细调节支持度、置信度等参数,不然会挖掘出很多很多的价值低的规则。
SlopeOne推荐算法的map-reduce
有关这个算法的原理可以参考网上或者本博客的另外一篇文章(http://www.cnblogs.com/kobedeshow/p/3553773.html ),关于这个算法的并行最关键的,计算item跟item之间的评分差异,下面以一个例子开始:
例如一个评分矩数据(用户,物品,评分)如下所示
A,one ,2
A,two ,3
A,three,1
B,one ,3
B,two ,5
C,one ,4
C,three,2
首先把该数据集打成{用户,[(物品1,评分),(物品2,评分),....,(物品n,评分)]}形式,很简单的一个map-reduce操作
物品one 物品two 物品three
用户A 2 3 1
用户B 3 5 ?
用户C 4 ? 2
当然真是的数据集肯定是非常稀疏的,这里只为讲清原理,接着对数据分片,分到不同的worker里面,这里假设3个,输入是[A,(one,2),(two,3),(three,1)],[B,(one,3),(two,5)],[C,(one,4),(three,2)]。
每一个map的操作输出<key,value> 对应了<(物品1,物品2),(评分1-评分2,1)> 最后面的1,是为了对(物品1,物品2) 计数1,上面第1个节点<(one,two),(-1,1)>,<(one,three),(1,1)>,<(two,three),(1,1)>; 第2个节点<(one,two),(-2,1)>,<(one,three ),(2,3,1)>; 第3个节点<(one,three ),(2,1)>。
接着可以进行一下combine操作,把key相同的value,评分差值相加,计数相加
最后进行reduce操作,得到物品跟物品之间的评分差
总结:slopeone在mahout0.9版本里面也被kill掉了,悲剧,难道太简单啦??关于该算法有另外一个变种就是weighted slopeone,其实就是在计算物品跟物品之间评分差的时候,进行了加权平均。
人脉二度推荐的map-reduce
最近社交类网站非常流行的给你推荐朋友/感兴趣的人,利用好社交关系,就不愁找不到好的推荐理由了,举个例子,假设A的好友是B,C,D,然而B的好友有E,C的好友有F,D的好友有E,那么如果要给A推荐好友的话,那么就会首推E了,因为B,C跟E都是好友,而F只是和C好友(有点关联规则里面支持度的味道)。OK,下面详解给A用户推荐好友的map-reduce过程
首先输入文件每行是两个id1,id2,假设id1认识id2,但是id2不认识id1,如果是好友的话,得写两行记录(方便记录单项社交关系)
A,B //A认识B
B,A //B认识A
A,C
C,A
A,D
D,A
B,E
E,B
C,F
F,C
D,E
E,D
第一轮map-reduce(为简单书写,下面只对与A有关的行为进行演示)
输入上面数据,输出<id,[(该id认识的人集合),(认识该id的人集合)]>
输出:<B,[(A),(E)]>,<C,[(A),(E)]>,<D,[(A),(F)]>
第二轮map-reduce
map输入上面数据,输出<[(该id认识的人),(认识该id的人)],id>
输出:<[(A),(E)],B>,<[(A),(E)],C>,<[(A),(F)],D>
reduce输入上面数据,输出<[(该id认识的人),(认识该id的人)],[id集合]>
输出:<[(A),(E)],[B,C]>,<[(A),(F)],[D]>
OK这样算法挖完了,id集合的长度作为二度人脉的支持度,可以从上面看到,A认识E,比A认识F更靠谱一点。
总结:还有很多其他的推荐算法诸如基于近邻的CF,模型的CF(矩阵分解),关于矩阵分解的,前段时间,LibSvm团队发表的Libmf,针对矩阵分解的并行化方面做出了非常好的贡献
参考资料:
1,《Parallelized Stochastic Gradient Descent》Martin A. Zinkevich、Markus Weimer、Alex Smola and Lihong Li
2,《Map-Reduce for Machine Learning on Multicore NG的一篇nips文章》
2,《Map-Reduce for Machine Learning on Multicore NG的一篇nips文章》
3,http://wenku.baidu.com/view/623ba70902020740be1e9b27.html
4,http://www.csdn.net/article/2014-02-13/2818400-2014-02-13
4,http://www.csdn.net/article/2014-02-13/2818400-2014-02-13
5,Pegasos:primal estimated sub-gradient solver for svm
6,machine learning in action
7,http://my.oschina.net/BreathL/blog/60725



 浙公网安备 33010602011771号
浙公网安备 33010602011771号