组合数学练习题

球盒问题总结：https://zhuanlan.zhihu.com/p/429815465

排列组合

知识补充

例题

除非有方法限制，否则从简单的排列组合模型开始尝试
难以下手的思路（主要是因为\(m,n\)固定了）：

• 用容斥则会简单问题复杂化，比这里(36题)还复杂.
• 用递推式：\(a_{m,n}=a_{m,n-1}+a_{m-1,n-1},\quad a_{0,0}=1,a_{x,0}=0,a_{0,x}=1\)

多重集的所有组合方式的计数，实际上可以用生成函数证明
上述题目的所有组合数即\((1+x+x^2+x^3)(1+x+x^2)(1+x)\)的系数，即可令\(x=1\)，得到\(4\times3\times2=24\)，至少有数即\(24-1=23\)

\(n\)个相同元素构成的线排列中取\(k\)个不相邻元素的不同取法是多少？环排列时取法又是多少？元素间隔不小于\(d\)时取法又是多少？

答案：线排列时的组合数是\(\begin{pmatrix}n+1-k\\k\end{pmatrix}\)，环排列时的组合数是\(\frac{n}{n-k}\begin{pmatrix}n-k\\k\end{pmatrix}\)，线排列而元素间间隔不小于\(d\)的组合数是\(\begin{pmatrix}n-(d-1)k+d-1\\k\end{pmatrix}\)
先讨论线排列的情况：
在这\(n\)个元素的左边添加\(2\)个元素，右边添加\(1\)个元素，即\(<n\times\cdot>\rightarrow<\cdot\cdot\quad n\times\cdot\quad\cdot>\)
然后放入\(k+1\)个隔板，每个隔板左边至少有\(2\)个元素，且末尾始终有\(1\)个隔板，比如当\(n=10\)时可以这样放\(<\cdot\cdot|\cdot\cdot|\cdot\cdot\cdot\cdot|\cdot\cdot\cdot|\cdot\cdot|>\)
于是这\(k+1\)个隔板将该线排列划分成\(k+1\)份，令第\(i\)份的数量为\(x_i\)，则\(\sum\limits_{i=1}^{k+1}x_i=n+3\quad(x_i\geq2)\)
所以原问题的组合数等于\(\sum\limits_{i=1}^{k+1}x_i=n+1-2k\quad(x_i\geq0)\)的解的个数，即\(\begin{pmatrix}n+1-k\\k\end{pmatrix}\)
再来讨论环排列的情况：
实际上环排列就是线排列的基础上去掉同时取首尾的情况
同时取首尾时，第\(2\)位和倒数第\(2\)位就不能取到，而剩下的中间部分可以看成是长度为\(n-4\)的线排列取\(k-2\)个不相邻元素的情况
故结果为\(\begin{pmatrix}n-k+1\\k\end{pmatrix}-\begin{pmatrix}(n-4)-(k-2)+1\\k-2\end{pmatrix}=\frac{n}{n-k}\begin{pmatrix}n-k\\k\end{pmatrix}\)
元素间隔不小于\(d\)时的情况：
第一问实际上是线排列而元素间间隔不小于\(2\)的组合数，所以第三问是第一问的扩展
实际上思路跟第一问相同，问题转化为\(\sum\limits_{i=1}^{k+1}x_i=n-dk+d-1\quad(x_i\geq0)\)的解的个数，即\(\begin{pmatrix}n-(d-1)k+d-1\\k\end{pmatrix}\)

鸽巢原理

知识补充

例题

参考Ramsey定理的使用和证明思路

关键点：\(n\)个数可以产生\(n-1\)个不同的差.

生成排列和组合

知识补充

例题

字典序的下一排列

• 右往左找第一个降的a
• a往右找比a大的最小数b
• 替换a和b，然后b后边的数升序排列

中介数就是大于\(1\)的从大到小的数的逆序数（顺序是从小到大），比如中介数\((120)\)意思是该排列有4个数（不妨设是\(\{1,2,3,4\}\)），其中\(4\)的逆序数是\(0\)，\(3\)的逆序数是\(2\)，\(2\)的逆序数是\(1\).

二项式系数

知识补充

\(\begin{pmatrix}-n\\k\end{pmatrix}=(-1)^{k}\begin{pmatrix}n-1+k\\n-1\end{pmatrix}\quad n\in\text{N}^+,k\in\text{N}\)
上述式子通常用在对项\((1+x+x^2+x^3+\cdots+x^{n-1})\)的化简，方便生成函数求系数（本质上是使用未展开的母函数取代对应的幂级数）
具体来说\(\left(\sum\limits_{i=0}^{n-1}x^i\right)=(1-x^n)(1-x)^{-1}\)，而当有\(t\)项时\((1-x)^{-t}\)的系数处理就可以使用上述式子

第二类斯特林数\(S(n,n-1)=\begin{pmatrix}n\\2\end{pmatrix}\)

例题

直接看成球盒模型，套第二类斯特林数
或者使用生成函数也很快得到答案

答案是780，使用乘除\((1-x)\)技巧简化运算的典型题目

容斥原理

知识补充

\[\begin{align*} P_k&=\sum\limits_{I\in C(n,k)}\left|\bigcap\limits_{i\in I}A_i\right|\\ Q_k&=\sum\limits_{I\in C(n,k)}\left|\left(\bigcap\limits_{i\in I}A_i\right)\cap\left(\bigcap\limits_{j\in\overline{I}}\overline{A_j}\right)\right|\\ Q_k&=\sum\limits_{i=0}^{n-k}(-1)^i\begin{pmatrix}k+i\\k\end{pmatrix}P_{k+i} \end{align*} \]

广义容斥原理：

• 定义：集合\(U\)是全集，\(U\)的元素有若干性质（每个元素包含的性质可能不同），现在有\(n\)个目标元素，\(A_i\)是至少包含第\(i\)个目标性质的元素的集合，\(P_k\)是至少包含\(k\)个目标性质的元素的集合，\(Q_k\)是恰好包含\(k\)个目标性质的元素的集合
• 关系：\(Q_0=U－Q_1\)即一般的容斥原理，它描述的是恰好包含\(0\)个目标性质的元素的集合（或只包含不具有目标性质的元素的集合）

错排、限排、禁排的基础都参考斯特林公式的思路（全集减补集得到目标集）

• 第二类Stirling数（\(n\)元集合的\(r\)-划分数，\(n\)个不同的球放入\(r\)个相同的盒）：\(S(n,r)=\frac{1}{r!}\sum\limits_{i=0}^{r}(-1)^{i}\begin{pmatrix}r\\i\end{pmatrix}(r-i)^{n}\)
• 错排：\(D_n=\sum\limits_{k=0}^{n}(-1)^{k}\begin{pmatrix}n\\k\end{pmatrix}(n-k)!=n!\sum\limits_{k=0}^n\frac{(-1)^k}{k!}\)，\(\lim\limits_{n \to \infty}D_n=\frac{n!}{e}\)
  \(D_n=(n-1)(D_{n-1}+D_{n-2})\)
• 限排：\(Q_n=\sum\limits_{k=0}^{n-1}(-1)^k\begin{pmatrix}n-1\\k\end{pmatrix}(n-k)!\)
  \(Q_n=D_n+D_{n-1}\)
• 禁排：\(p(X_{1},X_{2},\cdots,X_{n})=\sum\limits_{k=0}^n(-1)^{k}r_k(n-k)!\).（禁排是错排和限排的扩展）
  其中\(r_k\)表示选的\(i_1,i_2,\cdots,i_k\)行的所在列分别属于\(X_{i_1},X_{i_2},\cdots,X_{i_k}\)的方案数

若在棋盘\(C\)中，\(r_k(C)\)可以考虑使用棋盘多项式求解，即\(R(C)=\sum\limits_{k=0}^nr_k(C)x^k\).
\(r_k(C)\)的性质：

• \(r_0(C)=1\)
• \(r_1(C)\)等于\(C\)中的方格数
• \(r_k(C_1)=r_k(C_2)\)，其中\(C_1\)旋转或翻转可得到\(C_2\)
• \(r_k(C)=r_{k-1}(C_i)+r_k(C_l)\quad (k\geq1)\)，其中\(C_i\)为\(C\)去掉指定格所在的行和列之后剩余的棋盘，\(C_l\)是从棋盘去掉指定格之后剩余的棋盘
  通常用法是\(R(C)=R(C_i)+xR(C_l)\)
• \(r_k(C){=}\sum\limits_{i=0}^kr_i(C_1){\cdot}r_{k-i}(C_2)\)，其中棋盘\(C\)能拆成两个棋盘\(C_1\)和\(C_2\)，且它们的布棋方案相互独立
  通常用法是\(R(C)=R(C_1)R(C_2)\)

例题

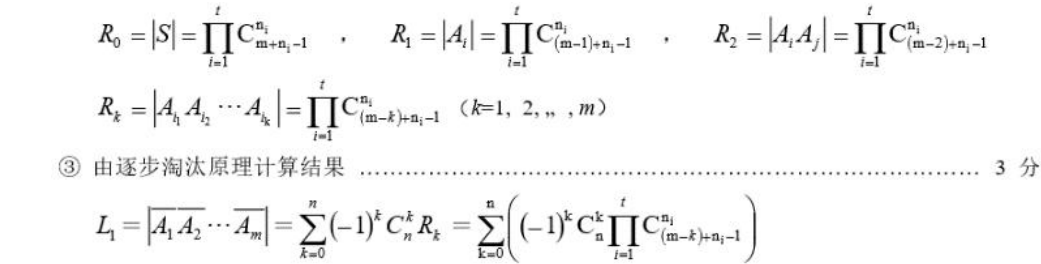
勘误：第③步\(\sum\limits_{k=0}^n\)应该是\(\sum\limits_{k=0}^m\)
直接排列组合难下手：
将题目转换，即对所有球做全排列，然后对每个排列进行划分（排列内空隙插入隔板，最后一个球后面固定放一个隔板，这样每个隔板左边的球就是各小盒装的球）
令\(n=\sum\limits_{i=1}^tn_i\)，计算全排列数\(p\)，\(p=\frac{n!}{\prod\limits_{i=1}^tn_i!}\)
然后内部间隔放\(m-1\)个隔板，固定最后放1个隔板，所以结果为\(\sum\limits_{k=0}^{C_{n-1}^{m-1}}\frac{p}{\prod\limits_{i=0}^m x_{k_i}}\)，其中\(x_{k_i}\)表示第\(k\)次划分时第\(i\)个盒子的球的数量.
PS：条件是多重不同球+不同盒子时，先做全排列再划分会有盒内球重复的情况，而盒子条件改为相同的话重复的情况会更多，因为盒子之间的球交换后不影响结果.

有难度的一题，关键点是计算\(k\)个\(A_i\)的交集的排列数
\(n\)个相邻数对中选择\(k\)个并再在其中选择不同的\(k\)个数的方案数\(\Leftrightarrow\)将\(n\)个相邻数对按顺序循环拼接起来选取不相邻的\(k\)个数的方案数
此外要求男女相间，否则答案是\(\sum\limits_{k=0}^n(-1)^kC_n^k2^k(2n-k-1)!\)

使用广义容斥原理

求重集\(B=\{4\cdot a,3\cdot b,4\cdot c,5\cdot d\}\)的\(r\)-组合数，其中\(r=12\)

上述答案用排列组合中全集减补集的思路，还可以用生成函数和直接排列组合方式去做
直接排列组合做法（分情况讨论）：

• \(a\)分别选\(0,1,2,3\)个的时候，即要从\(b,c,d\)里分别选出\(12,11,10,9\)个，即从\(b,c,d\)里分别筛掉\(0,1,2,3\)个，因此这里的方案数有\(F(3,0)+F(3,1)+F(3,2)+F(3,3)=1+3+6+10=20\)
• \(a\)选\(4\)个时，继续分情况讨论：
  • \(c\)分别选\(0,1,2,3\)个的时候，即要从\(b,d\)里分别选出\(8,7,6,5\)个，即从\(b,d\)里分别筛掉\(0,1,2,3\)个，因此这里的方案数有\(F(2,0)+F(2,1)+F(2,2)+F(2,3)=1+2+3+4=10\)
  • \(c\)选\(4\)个的时候，剩下只能让\(b\)分别选\(0,1,2,3\)个，对应\(d\)选\(4,3,2,1\)个，这里的方案数只有\(4\)种

综上方案数有\(20+10+4=34\)种
使用生成函数方法（可以配合乘除\((1-x)\)技巧优化运算）：

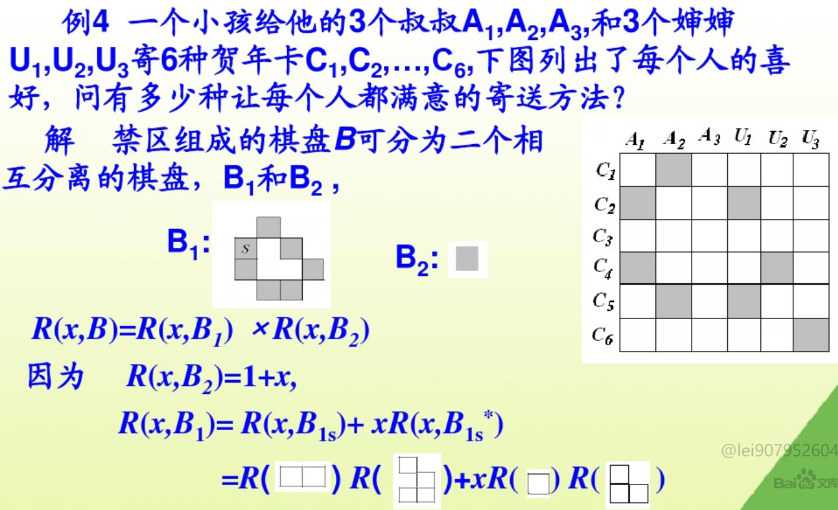
棋盘禁排的技巧：
棋盘的乘法拆解只要两个棋盘相互独立不要求在原棋盘上连续
交换行和列不影响答案，故棋盘的加法拆解或乘法拆解之后进行行列的移动有助于计数

递推关系和生成函数

知识补充

解方程求递推关系式通项公式：

• 解齐次方程：
  
  
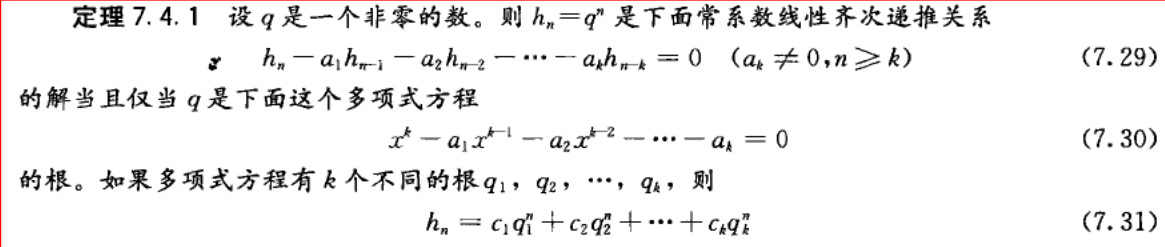
• 解非齐次方程：
  

类似于\(a_n=a_{n-1}+n^t\)的递推关系，会遇到齐次通解得到\(1\)而非齐次的特解却无解的情况
此时可令特解为\(\sum\limits_{i=0}^{t+1}c_in^i\)，继续求解
或者反复使用递推关系把非齐次变齐次再重新求解

生成函数求递推关系式通项公式：

• 令母函数\(G(x)=\sum\limits_{i=0}^\infty a_ix^i\)
• 代入初始值\(a_0,a_1,\cdots,a^t\)
• 假设递推关系为\(\sum\limits_{i=0}^{t+1}k_ia_{n-i}=0\)，则求得\(\left(\sum\limits_{i=0}^{t+1}k_ix^i\right)G(x)=\sum\limits_{i=0}^{t}\left(\sum\limits_{j=0}^{i}k_ja_{i-j}\right)x^i\)
• 求解\(G(x)=\frac{\sum\limits_{i=0}^{t}\left(\sum\limits_{j=0}^{i}k_ja_{i-j}\right)x^i}{\sum\limits_{i=0}^{t+1}k_ix^i}\)，结果表示为幂级数形式，\(a_n\)即第\(x^n\)的系数表达式

使用生成函数时排列和组合的区分：

• 根本在于选取的物件是否有区别
• 球盒模型中（把\(n\)个球放到\(m\)个盒）：
  盒不同的条件下，若球不同则是排列问题，若球相同则是组合问题.
  盒相同则是对应在盒不同的条件下除以盒的排列.
• 一列木块染色中，各染色数量相同情况下交换两个染色是不同的方案，故是排列问题.

例题

该题用容斥原理也能做，但得到的答案为：\(5^n-\sum\limits_{d=2}^n\left[(-1)^n\sum\limits_{k=1}^{\left\lceil\frac{n}{d}\right\rceil}4^{n-kd}\begin{pmatrix}(n-(d-1))-(d-1)k+d-1\\k\end{pmatrix}\right]=5^n-\sum\limits_{d=2}^n\left[(-1)^n\sum\limits_{k=1}^{\left\lceil\frac{n}{d}\right\rceil}4^{n-kd}\begin{pmatrix}n-(d-1)k\\k\end{pmatrix}\right]\)
如果是直接用排列组合的话，应该是这个形式：\(5^n-\sum\limits_{d=2}^n\sum\limits_{k=1}^{\left\lceil\frac{n}{d+1}\right\rceil}4^{n-dk}\begin{pmatrix}(n-(d-1))-dk+d\\k\end{pmatrix}=5^n-\sum\limits_{d=2}^n\sum\limits_{k=1}^{\left\lceil\frac{n}{d+1}\right\rceil}4^{n-dk}\begin{pmatrix}n-dk+1\\k\end{pmatrix}\)

求\(S_n=1^2+2^2+\cdots+n^2\)的通项

齐次通解得到\(1\)而非齐次的特解却无解的情况

对于求\(F_n-F_{n-1}=n^k\)的通项，有两种做法
第一种：反复使用递推关系把非齐次变齐次再重新求解：

• 先得到齐次\(\sum\limits_{i=0}^{k+2}\begin{pmatrix}k+2\\i\end{pmatrix}F_{n-i}=0\)
• 因为特征值全为1，不妨令\(F_n=\sum\limits_{i=0}^{k+1}c_i\begin{pmatrix}n\\i\end{pmatrix}\)
• 求解\(c\)，实际上\(c_i=F_i-\sum\limits_{j=0}^{i-1}c_j\)

第二种：

• 直接令特解为\(\sum\limits_{i=0}^{t+1}c_in^i\)，回代\(F_n-F_{n-1}=n^k\)求特解
• 最后再求通解

求\(a_n=a_{n-1}+2(n-1)\quad(n\geq2),a_1=2\)的通项

齐次通解得到\(1\)而非齐次的特解却无解的情况

答案：\(\begin{cases}f\left(n\right)=\left(k-1\right)f\left(n-2\right)+\left(k-2\right)f\left(n-1\right)\left(n\geq4\right)\\f\left(2\right)=k\left(k-1\right),f\left(3\right)=k\left(k-1\right)\left(k-2\right)\end{cases}\)

求从\(n\)个不同物体中允许重复地选取\(r\)个物体，但每个物体出现偶数次的方式数

使用生成函数求解：

也可以直接使用无限重集的组合求法一步到位，即一次取两个相同的物体，取\(\frac{r}{2}\)次，则\(\begin{pmatrix}n+\frac{r}{2}-1\\\frac{r}{2}\end{pmatrix}\)

经典的单色奇偶染色限制问题.

勘误：\(a_n=\frac{1}{2}\left(7\cdot8^{n-1}+9\cdot10^{n-1}\right)\)
之所以会有这个错误，是因为在建立递推公式时\(a\)的下标和\(x\)的次数未统一，实际上如果按照递推公式那样（即\(a_1=8\)），\(a_n\)应该取\(x^{n-1}\)的系数才对
如果递推公式中统一\(a\)的下标和\(x\)的次数，则应该这样推：

\[\begin{align*} (1-8x)A(x)&=a_1x+\sum\limits_{k=2}^\infty\left(a_k-8a_{k-1}\right)x^k\\ (1-8x)A(x)&=8x+\sum\limits_{k=2}^\infty\left(9\times10^{k-2}\right)x^k\\ A(x)&=\frac{1}{2}\sum\limits_{k=1}^\infty\left(7\times8^{n-1}+9\times10^{n-1}\right)x^n \end{align*} \]

另外，递推公式的\(a_n=8a_{n-1}+9\times10^{n-2}\)应该这样理解：

• 令\(b_n\)是\(n\)位正整数中含有奇数个\(5\)的正整数个数，\(a_n^*,b_n^*\)是数字串，与\(a_n,b_n\)不同的是它们考虑最高位为\(0\)的情况
• 则显然有这些等式成立：
  • \(a_n+b_n=9\times10^{n-1}\)
  • \(a_n=a_n^*-a_{n-1}^*\)
  • \(b_n=b_n^*-b_{n-1}^*\)
  • \(a_n=8a_{n-1}^*+b_{n-1}^*\)
• 利用这些等式进行推导：
  \[\begin{align*} a_n&=8a_{n-1}^*+b_{n-1}^*\\ &=8(a_{n-1}+a_{n-2}^*)+(b_{n-1}+b_{n-2}^*)\\ &=8a_{n-1}+(8a_{n-2}^*+b_{n-2}^*)+b_{n-1}\\ &=8a_{n-1}+a_{n-1}+b_{n-1}\\ &=8a_{n-1}+9\times10^{n-1} \end{align*} \]

最后实际上该题直接使用组合做会更快：

\[\begin{align*} a_n^*是多项式&\sum\limits_{k=0}^nC_n^k9^{n-k}中k为偶数的项的总和\\ b_n^*是多项式&\sum\limits_{k=0}^nC_n^k9^{n-k}中k为奇数的项的总和\\ 故a_n^*+b_n^*&=(9+1)^n=10^n\\ a_n^*-b_n^*&=(9-1)^n=8^n\\ 即a_n^*&=\frac{10^n+8^n}{2}\\ a_n&=a_n^*-a_{n-1}^*\\ &=\frac{1}{2}\left(7\times8^{n-1}+9\times10^{n-1}\right) \end{align*} \]

也可以考虑使用生成函数，参考上一题做法.

一列有\(n\)个木块，染成\(A,B,C,D\)四种中的一种颜色，其中\(A\)占奇数个，\(B\)占偶数个，\(C\)占\(3\)的倍数个，\(D\)没有限制，问一共有几个方案

答案：

\[\begin{align*} A(x)&=\frac{e^x-e^{-x}}{2}\\ B(x)&=\frac{e^x+e^{-x}}{2}\\ C(x)&=\sum\limits_{k=0}^{\infty}\frac{x^{3k}}{(3k)!}=\frac{1}{3}\left(e^x+e^{e^{\frac{2\pi}{3}i}x}+e^{e^{\frac{4\pi}{3}i}x}\right)\\ D(x)&=e^x\\ A(x)B(x)C(x)D(x)&=\frac{\left(e^{3x}-e^{-x}\right)\left(e^x+e^{e^{\frac{2\pi}{3}i}x}+e^{e^{\frac{4\pi}{3}i}x}\right)}{12}\\ &=\sum\limits_{n=1}^{\infty}\frac{4^n+\left(\frac{5}{2}+\frac{\sqrt{3}}{2}i\right)^n+\left(\frac{5}{2}-\frac{\sqrt{3}}{2}i\right)^n-\left(-\frac{3}{2}+\frac{\sqrt{3}}{2}i\right)^n-\left(-\frac{3}{2}- \frac{\sqrt{3}}{2}i\right)^n}{12}\cdot\frac{x^n}{n!}\ \end{align*} \]

故答案为：
\(\frac{4^n+\left(\frac{5}{2}+\frac{\sqrt{3}}{2}i\right)^n+\left(\frac{5}{2}-\frac{\sqrt{3}}{2}i\right)^n-\left(-\frac{3}{2}+\frac{\sqrt{3}}{2}i\right)^n-\left(-\frac{3}{2}-\frac{\sqrt{3}}{2}i\right)^n}{12}\)

Polya计数

知识补充

通用解法步骤：

• 通过旋转和反射(翻转)遍历每种置换，写出它们的类型单项式\(z_1^{e_1}z_2^{e_2}\cdots z_n^{e_n}\)或直接写成\(1^{e_1}2^{e_2}\cdots n^{e_n}\)，其中\(z_i^{e_i}\)代表\(i\)阶循环的个数
• 写出置换集\(G\)的循环指数\(P_G(z_{1},z_{2},\cdots,z_{n})=\frac{1}{|G|}\sum\limits_{f\in G}z_{1}^{e_{1}}z_{2}^{e_{2}}\cdots z_{n}^{e_{n}}\)
• 根据求解任务使用循环指数
  • 若任务是用\(k\)种颜色染色，每种颜色没有染色次数限制，则方案数为\(P_G(k,k,\cdots,k)\)
  • 若任务是用\(k\)种颜色染色，限制第\(i\)种颜色只能染色\(t_i\)次，则先用\(z_{j}=u_{1}^{j}+\cdots+u_{k}^{j}\quad(j=1,2,\cdots,n)\)进行代换，展开\(P_G(z_{1},z_{2},\cdots,z_{n})\)后，\(u_1^{t_1}u_2^{t_2}\cdots u_k^{t_k}\)的系数即为所求

例题

二分图

知识补充

定义：

• 点覆盖\(S\)：给定图\(G=(V,E)\)，\(S\subseteq V\)，且每一条边至少有一个端点在\(S\)中
  最小点覆盖即\(|S|\)最少的\(S\)
• \(X,Y\)：假设二分图是左右两排结点的形式，这里分别特定为二分图中的左边的结点和右边的结点
• \(M\)：二分图中的一个匹配.
• 标注：运用算法过程中，从\(X\)端的\(x_i\)连到\(Y\)端的\(y_i\)则给\(y_i\)标注\((x_i)\)，从\(Y\)端的\(y_i\)连到\(X\)端的\(x_i\)则给\(x_i\)标注\((y_i)\)
• 突破：\(Y\)中有一个已标注但不与\(M\)中任意边相遇的顶点
• 非突破：算法停止，突破没有出现，即\(Y\)中的每一个已标注顶点与\(M\)中的某条边相遇

匹配算法流程：

• 找一次\(M\)的交错路径:
  • 开始从\(X\)端的不与\(M\)相遇的结点出发（没有就结束）
  • 在\(X\)端和\(Y\)端反复跳动标注（找不到结点标注就结束）。从\(X\)端出发则找\(Y\)端未标记且连线不属于\(M\)的结点，从\(Y\)端出发则找\(X\)端未标记且连线属于\(M\)的结点，每次找到结点都要进行标注
• 不断尝试找\(M\)的交错路径\(M_\gamma\)以得到新匹配代替\(M\)。若结束时存在突破则存在交错路径\(M_\gamma\)且新的匹配是\((M-M_\gamma)\cup\overline{M_\gamma}\)，若结束时没有突破出现，则算法结束。

最小覆盖和最大匹配关系定理：假设在匹配算法中非突破发生。设\(X^{un}\)是由\(X\)中所有没有被标注的顶点组成的，\(Y^{lab}\)是由\(Y\)中所有已标注顶点组成的，且令\(S=X^{un}\cup Y^{lab}\)，则下面两个结论都成立：

• \(S\)是二分图\(G\)的最小覆盖
• \(|M|=|S|\)且\(M\)是最大匹配

例题