Fisher判别准则
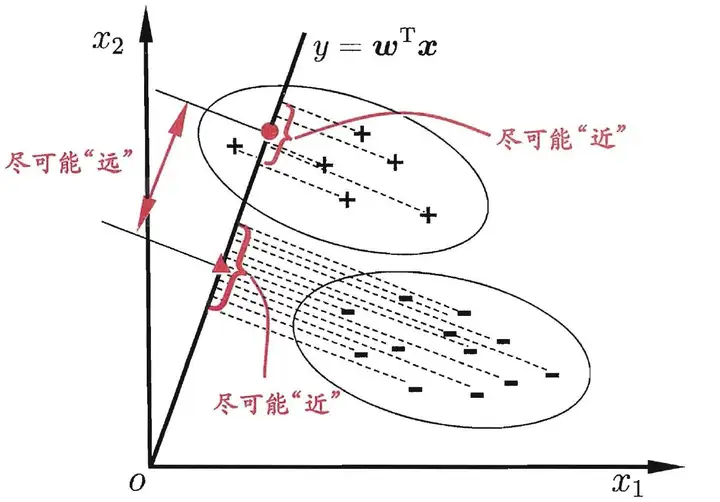
Fisher判别分析的思想:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、不同类样例的投影点尽可能远离。在对新样本进行分类时,将其投影到同样的这条直线上,再根据新样本投影点的位置来确定它的类别。
Fisher准则得到的结果是“次优”,而非“最优”。这与Fisher算法的“小样本问题”和“次优性问题”有关。
最优分界面的求解步骤
假设有\(n\)个样本\(X\in\textbf{R}^{k\times n}\)及其标签\(y\in\textbf{R}^{1\times n}\),\(X_i\)和\(y_i\)分别代表第\(i\)个样本及其标签
由Fisher准则得到的分界面函数为:
\[\begin{gather}
g\left(x\right)=W\cdot x+b=0,\quad x\in\textbf{R}^{k\times 1}
\end{gather}
\]
该最优分界面的目标函数为:
\[\begin{gather}
\begin{split}
s.t.\quad y_i\cdot(\begin{array}{c}W\cdot X_i+b\end{array})-1\geq0\\
f(W)=\frac{1}{2}(W\cdot W^T)
\end{split}
\end{gather}
\]
用多元Lagrange函数求极值:
(只考虑约束条件中等号成立的情况,不成立的情况直接对目标函数求偏导得到的\(W=0\)无意义)
\[\begin{gather}
L(W,b,\alpha)=\frac12(W\cdot W)-\sum\limits_{i=1}^n\alpha_i\left[y_i(W\cdot X_i+b)-1\right]
\label{Lagrange-ori}
\end{gather}
\]
对\(L(W,b,\alpha)\)的\(W\)和\(b\)分别求偏导:
\[\begin{gather}
\left.\left\{
\begin{aligned}
&\frac{\partial L}{\partial W}=W-\sum_{i=1}^n\alpha_iy_iX_i=0\\
&\frac{\partial L}{\partial b}=\sum_{i=1}^n\alpha_i y_i=0
\end{aligned}
\right.\right.
\label{Lagrange-ori-d}
\end{gather}
\]
即
\[\begin{gather}
\left.\left\{
\begin{aligned}
&W=(\alpha\odot y)X^T\\
&y\alpha^T=0
\end{aligned}
\right.\right.
\label{Lagrange-ori-d2}\\
where\quad\odot\;is\;Hadamard\;Product\notag
\end{gather}
\]
将\((\ref{Lagrange-ori-d})\)回代到式\((\ref{Lagrange-ori})\)中,转化为参数\(\alpha\)的优化问题:
(在得到不考虑\(\alpha\)偏导的原函数极值\(L(\alpha)\)后,再求\(L(\alpha)\)关于\(\alpha\)的极值,即部分极值后再求极值)
\[\begin{equation}
\begin{split}
s.t.\quad\sum_{i=1}^n\alpha_iy_i&=0,\quad\alpha_i\geq0\\
A(\alpha)=L\left(W(\alpha),b(\alpha),\alpha\right)&=\sum\limits_{i=1}^{n}\alpha_{i}-\frac{1}{2}\left(\sum\limits_{i=1}^{n}\alpha_{i}y_{i}X_{i}\right)^2\\
&=\sum\limits_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum\limits_{1\leq i\leq n\atop 1\leq j\leq n}Z_{ij}\alpha_{i}\alpha_{j}\\
&=\sum\limits_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum\limits_{i=1}^nZ_{ii}\alpha_{i}^2-\sum\limits_{1\leq i < j\leq n}Z_{ij}\alpha_{i}\alpha_{j}\\
where\quad Z&=(X^TX)\odot(y^Ty)
\end{split}
\end{equation}
\]
对\(A(\alpha)\)求偏导,同时考虑约束条件\(\sum_{i=1}^n\alpha_iy_i=0\):
\[\begin{gather}
\left.\left\{
\begin{aligned}
&\sum_{i=1}^n\alpha_iy_i=0\\
&\frac{\partial A(\alpha)}{\partial\alpha_i}=1-\sum\limits_{j=1}^nZ_{ij}\alpha_j=0\\
&\cdots
\end{aligned}
\right.\right.
\end{gather}
\]
即
\[\begin{gather}
\begin{bmatrix}y\\Z\end{bmatrix}\alpha^T=\begin{pmatrix}0\\1\\1\\\cdots\\1\end{pmatrix}
\end{gather}
\]
再确保约束条件\(\alpha_i\geq0\)和\(y\alpha^T=0\)的情况下,找到剩下矛盾的等式拆成不同的等式联立,尝试求解\(\alpha\)
(通常有多种联立方式,而每种联立方式又有多个解,找到其中一种满足约束条件的\(\alpha\)解即可)
将\(\alpha,X,y\)代回到式\((\ref{Lagrange-ori-d2})\)中,解出\(\hat{W}\)
找出\(\alpha\)中所有大于0的\(\alpha_p\)及其对应样本\(X_p\)和标签\(y_p\),并保证标签不重复(随机去除重复的)
从支持向量的约束条件\(\begin{aligned}y_i\cdot(W\cdot X_i+b)-1=0\end{aligned}\)有
\[\begin{gather}
\begin{aligned}
\hat{b_p}&=y_p^{-1}-\hat{W}X_p,\quad y_i\neq 0\\
\hat{b}&=\frac{1}{P}\sum\limits_{p=1}^P\hat{b_p}\\
where\quad &P\;is\;the\;number\;of\;all\;the\;\hat{b_p}
\end{aligned}
\end{gather}
\]
最后得到最优分界面\(\hat{g}\left(x\right)=\hat{W}\cdot x+\hat{b}=0,\quad x\in\textbf{R}^{k\times 1}\)
小结
计算顺序:\(Z\to\alpha\to\hat{W}\to\hat{b}\)
\[\begin{aligned}
Z&=(X^TX)\odot(y^Ty)\\
\begin{bmatrix}y\\Z\end{bmatrix}\alpha^T&=\begin{pmatrix}0\\1\\1\\\cdots\\1\end{pmatrix}\\
\hat{W}&=(\alpha\odot y)X^T\\
\hat{b}&=\frac{1}{P}\sum\limits_{p=1}^P\left(\frac{1}{y_p}-\hat{W}X_p\right)
\end{aligned}
\]
例题
\[\begin{gather*}
X=\begin{pmatrix}0 &1 &2 &0 \\0 &0 &0 &2 \\\end{pmatrix},\quad y=(1,1,-1,-1)\\
令Q=\begin{pmatrix}0 &1 &-2 &0 \\0 &0 &0 &-2 \\\end{pmatrix},则\\
Z=Q^TQ=\begin{pmatrix}0 &0 &0 &0 \\0 &1 &-2 &0 \\0 &-2 &4 &0 \\0 &0 &0 &4 \\\end{pmatrix}\\
\begin{bmatrix}y &0 \\Z &1 \\\end{bmatrix}=\begin{pmatrix}1 &1 &-1 &-1 &0 \\0 &0 &0 &0 &1 \\0 &1 &-2 &0 &1 \\0 &-2 &4 &0 &1 \\0 &0 &0 &4 &1 \\\end{pmatrix}\\
去掉无法操作的行(这里是第二行),确保约束条件(第一行)然后拆开线性相关部分(第三、四行)\\
(PS:这里的线性相关部分从X入手比较快,此外解方程时可以考虑待定最右列的值)\\
\begin{pmatrix}1 &1 &-1 &-1 &0 \\0 &1 &-2 &0 &1 \\0 &0 &0 &4 &1 \\\end{pmatrix},\quad\begin{pmatrix}1 &1 &-1 &-1 &0 \\0 &-2 &4 &0 &1 \\0 &0 &0 &4 &1 \\\end{pmatrix}\\
指定\alpha_1=0则,又由于约束条件\alpha_i\geq0,所以只有第二个拆开的部分满足要求,并解得\alpha=(0,1,\frac{3}{4},\frac{1}{4})\\
\begin{aligned}
\hat{W}=(\alpha\odot y)X^T&=\left((0,1,\frac{3}{4},\frac{1}{4})\odot (1,1,-1,-1)\right)X^T\\
&=(0,1,-\frac{3}{4},-\frac{1}{4})\begin{pmatrix}0 &0\\ 1 &0\\ 2 &0\\ 0 &2 \\\end{pmatrix}\\
&=(-\frac{1}{2},-\frac{1}{2})\\
\end{aligned}\\
选取\alpha_2和\alpha_3所代表的样本,则\\
\begin{aligned}
\hat{b}=\frac{1}{P}\sum\limits_{p=1}^P\left(\frac{1}{y_p}-\hat{W}X_p\right)&=\frac{1}{2}\left(\frac{1}{y_2}-\hat{W}X_2+\frac{1}{y_3}-\hat{W}X_3\right)\\
&=\frac{1}{2}\left(1-(-\frac{1}{2})+(-1)-(-1)\right)\\
&=\frac{3}{4}\\
\end{aligned}\\
因此,\hat{g}\left(x\right)为:\\
\begin{aligned}\hat{W}\cdot x+\hat{b}&=0\\
(-\frac{1}{2},-\frac{1}{2})x+\frac{3}{4}&=0\\
2x_1+2x_2-3&=0
\end{aligned}\\
\end{gather*}
\]
练手:
\[\begin{gather*}
X=\begin{pmatrix}0 &1 &0 &2 &0 \\0 &0 &1 &0 &2 \\\end{pmatrix},\quad y=(1,1,1,-1,-1),\quad 3x_1+3x_2-4=0\\
X=\begin{pmatrix}0 &0 &3 &0 \\0 &1 &0 &3 \\\end{pmatrix},\quad y=(1,1,-1,-1),\quad x_1+x_2-2=0\\
X=\begin{pmatrix}0 &1 &1 &0 &0 &0 \\0 &0 &0 &0 &1 &1 \\0 &0 &1 &1 &0 &1 \\\end{pmatrix},\quad y=(1,1,1,-1,-1,-1),\quad 2x_2-2x_6+1=0
\end{gather*}
\]
参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号