分类与回归

分类与回归

分类：对数据集进行学习并构造一个拥有预测功能的分类模型，用于预测未知样本的类标号
回归：可以对预测变量和响应变量之间的联系建模（包括线性回归、非线性回归、逻辑回归等）

分类与回归的区别：

• 分类预测的输出为类标号，回归预测的输出为连续属性值
• 分类是监督学习，回归是无监督学习

分类算法有：

• 基于决策树分类
• 贝叶斯分类
• K-最近邻分类
• *神经网络
• *支持向量机
• *集成学习

基于决策树分类

相关概念

决策树：是一种树型结构，包括决策节点(内部节点)、分支和叶节点三个部分

• 决策节点：通常对应于待分类对象的某个属性，在该属性上的不同测试结果对应一个分支
• 分支：决策结点不同取值
• 叶节点：表示一种可能的分类结果

决策树：

构建决策树

两个问题：属性选择、树大小合适
经典的构建算法：ID3、C4.5、CART等

决策树的属性选择

常见的选择标准：信息增益、Gini系数

获得大小合适的树

两种获取方法：定义树的停止生长条件、对完全生长决策树进行剪枝

• 定义停止生长条件：
  最小划分实例数：划分的子集大小小于该数时停止
  划分阈值：父节点与划分的子节点的值的差小于阈值时停止
  最大树深度
• 剪枝：对子树评估，若去掉子树后整个决策树表现更好，则剪掉该子树

节点划分

• 离散属性：每个可能取值一个分支
• 连续属性：给定阈值，小于等于阈值为一个分支，大于阈值为另一个阈值
• 离散属性构成二叉树：取属性的可能取值为一个集合，属于该集合为一个分支yes，不属于该集合为另一个分支no

ID3分类算法

概念：使用信息增益作为属性的选择标准

信息熵

概念：属性信息量的度量（或不确定性的度量），信息量越大熵越大
熵越小表示样本对目标属性的分布越纯，熵越大表示样本对目标属性分布越混乱

$$E(S)=E(p_{1},p_{2},...,p_{m})=-\sum_{i=1}^{m}p_{i}log_{2}p_{i} \\E是Entropy的缩写，E()即Entropy()，是训练集S对目标属性C的信息熵 \\目标属性C有m个可能类标号值 \\p_{i}为C_{i}类在样本中出现的概率$$

信息增益

概念：样本划分前后的信息熵差值（越大越好）

$$G(S,A)=E(S)-E_{A}(S) \\E_{A}(S)=\sum_{i=1}^{k}\frac{|S_{i}|}{|S|}E(S_{i}) \\G()即Gain()，是按属性A划分样本集S的信息增益 \\E_{A}(S)是S按属性A划分后的k个样本子集的熵 \\|S_{i}|和|S|分别是集合S_{i}和S的大小$$

ID3建立决策树

步骤：

1. 检测所有属性，选择信息增益最大的属性产生决策树结点，由该属性的不同取值建立分支
2. 对各分支的子集递归调用该方法建立决策树结点的分支，直到所有子集仅包含同一个类别的数据为止

*缺失值处理

方法一：抛弃数据集中具有缺失值的数据
方法二：以某种方式填充缺失的数据（如使用属性的平均值代替）

*特点

优点：简单，学习能力强
缺点：只能处理分类属性数据，无法处理连续型数据；生成决策树时偏向选择具有较多分枝的属性

C4.5分类算法

概念：使用信息增益率作为属性的选择标准

与ID3相比，算法步骤中除了属性选择依据由信息增益变为信息增益率外，其余一样

信息增益率

相比信息增益，不仅考虑信息增益的大小，还兼顾为获得信息增益所付出的“代价”（消除属性取值数目所带来的影响），但同样是越大越好

$$GR(A)=\frac{G(A)}{SE(A)} \\SE(A)=-\sum_{i=1}^{k}\frac{|S_{i}|}{|S|}log_{2}\frac{S_{i}}{S} \\GR()即GainRatio()，是数据集S关于属性A的信息增益率 \\G(A)即G(S,A)，是数据集S关于属性A的信息增益 \\SE()即SplitE()，是数据集S关于属性A的分裂信息$$

*处理数值型属性

步骤：

1. 对属性进行递增排序，把每对相邻值的中值点看作可能的分裂点
2. 计算每个分裂点的$E_A{S}$，选择最小的$E_A{S}$对应的分裂点作为最佳分类点

*缺失值处理

与ID3不同，采用概率的方法，而不是简单地将最常见的值替代该缺失值

假设S为训练集，属性A存在缺失值，属性A的信息增益计算方法改为：

$$G(A)=r_{A}\times(E(S)-E_{A}(S)) \\SE(A)=-\left ( \sum_{i=1}^{k}\frac{|S_{i}|}{|S|}log_{2}\frac{|S_{i}|}{|S|} \right )-\frac{|S_{unknow}|}{|S|}log_{2}\frac{|S_{unknow}|}{|S|} \\r_{A}是属性A在样本集中不空值的比率 \\把A的属性类别值未知的样本子集作为类别S_{unknow}$$

*C4.5剪枝

C4.5采用的是后剪枝，即决策树得到充分生长，再根据一定规则，剪去那些不具有代表性的的子树或叶子节点（如使用子树中最频繁的类B代替整个子树）

CART分类算法

概念：使用Gini系数作为属性的选择标准，采用二元递归划分方法，构造二叉树

Gini系数

Gini系数：度量对某个属性变量测试输出的两组取值的差异性
对于节点t，G(t)越小越好（Gini系数越小不纯度越高）

$$G(t)=1-\sum_{j=1}^{k}p^{2}(j|t) \\G(t)是节点t的Gini系数 \\k为当前属性下测试输出的类别数 \\p(j|t)为节点t中样本测试输出取类别j的概率$$

节点在分枝条件ξ下的差异性损失$\Delta G(\xi ,t)$越大越好（越大则节点越纯），即$G_{\xi}(t)$越小越好

$$\Delta G(\xi ,t)=G(t)-G_{\xi}(t) \\G_{\xi}(t)=\frac{|S_{R}|}{|S_{L}|+|S_{R}|}G(t_{R})+\frac{|S_{L}|}{|S_{L}|+|S_{R}|}G(t_{L}) \\\Delta G(\xi ,t)为条件\xi 下t节点的差异性损失 \\\xi 为节点t的一个属性分支条件，该条件将t节点分到左分支S_{L}和右分支S_{R}$$

属性选择

计算每个属性在最佳取值划分下的差异性损失，选择差异性损失最大的属性作为节点，最大的不止一个属性时选择最先出现的属性
一个节点只能代表一个属性，一个属性只能出现在一个节点中（不管属性有多少类别取值）

属性的最佳划分：

• 数值属性：
  1. 先升序排序
  2. 取相邻数值的中间值作为分裂点，将样本分为两组
  3. 选择Gini系数值最小的分裂点作为属性的最佳分裂点
• 分类属性：
  1. 将属性的多类别合并成两个类别，形成超类
  2. 选择Gini系数值最小的合并方式作为该属性的最佳超类划分

属性划分得到的决策树：

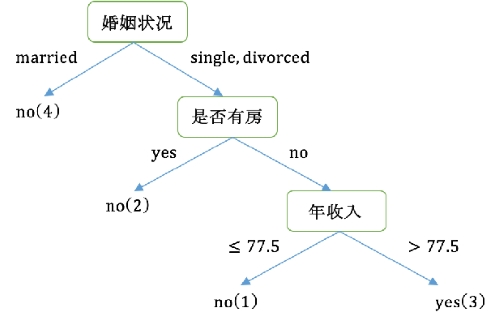
贝叶斯分类

概念：利用概率统计进行学习分类的方法
主要算法有：朴素贝叶斯分类算法、贝叶斯信念网络分类算法

原理

贝叶斯定理：$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(X|Y)P(Y)}{P(X)}$

设数据集为D，对应属性集$U=\{A_{1},A_{2},...,A_{n},C\}$，$A_{1},A_{2},...,A_{n}$是样本的属性变量，C是类标号属性变量，可取$C_{1},C_{2},...,C_{m}$

则贝叶斯的作用是将样本X分配给$C_{i}$，当且仅当$P(C_{i}|X)>P(C_{j}|X)$，$(1\leq j \leq m,i\neq j)$
即求$P(C_{i}|X)=\frac{P(X|C_{i})P(C_{i})}{P(X)}$的最大值，等价于求$P(X|C_{i})P(C_{i})$的最大值
假设属性相互独立，即有$P\left ( X\mid C_{i} \right )=P\left ( X_{1},X_{2},...,X_{n}\mid C_{i} \right )=\prod _{k=1}^{n}P(X_{k}\mid C_{i})$

步骤（伪代码）

for j=1 to m
	计算X属于每一个类别Cj的概率P(X|Cj);
	计算训练集中每个类别Cj的概率P(Cj);
	计算概率值P(X,Cj)=P(X|Cj)P(Cj);
end for
选择概率值P(X,Cj)最大的Cj作为类别输出

*条件概率的Laplace估计

作用：处理条件概率$P(X|C_{j})$为0或很小的情况

两种Laplace估计定义：

1. 当存在某个条件概率很小时使用Laplace估计，让每个需要的计数加1，然后再计算每个条件概率
2. 条件概率改变为：

$$P(X_{i}\mid C_{j})=\frac{n_{c}+l \times p}{n+l} \\n是类C_{j}的训练样本总数，n_{c}是类C_{j}的训练样本中属性变量A_{i}取值为X_{i}的样本数 \\l是称为等价样本大小的参数，p是用户指定的参数$$

ps：按照一般题目来看，可以有$l=n$，$p=\frac{1}{l}$

*连续属性的解决方法

可以把连续属性离散化
可以假设连续的变量服从某种概率分布（如正态分布），可以用均值和方差来计算条件概率

*朴素贝叶斯分类算法的特点

优点：易于实现、大多数结果比较好
缺点：算法成立前提是假设各属性之间相互独立

k-最近邻分类算法（KNN）

概念：基于实例的学习算法，直接用训练集对数据样本进行分类，确定其类别标号

基本思想：对于未知类标号的样本，按欧式距离找出它在训练集中的k个最近邻，将未知样本赋予k最近邻中出现次数最多的类别号

算法步骤

设训练集D，测试集Z，最近邻数目为k
每个样本可以表示为$(x,y)$的形式，即$(x_{1},x_{2},...,x_{n},y)$
其中$(x_{1},x_{2},...,x_{n})$表示样本的n个属性，y表示样本的类标号

1. 对每个测试样本$z=(x',y')\in Z$，计算z与每个训练样本$(x,y)\in D$间的距离$d=(x',x)$
2. 选择离Z最近的k个近邻集合$D_{Z}\in D$
3. 得到$D_{Z}$中样本的多数类的类标号作为结果

*KNN算法的特点

优点：思路简单，易于实现
缺点：对每个属性都要指定相同的权重；时间复杂度为$O(n^{2})$