概率论笔记(4)
第四章 随机变量的数字特征
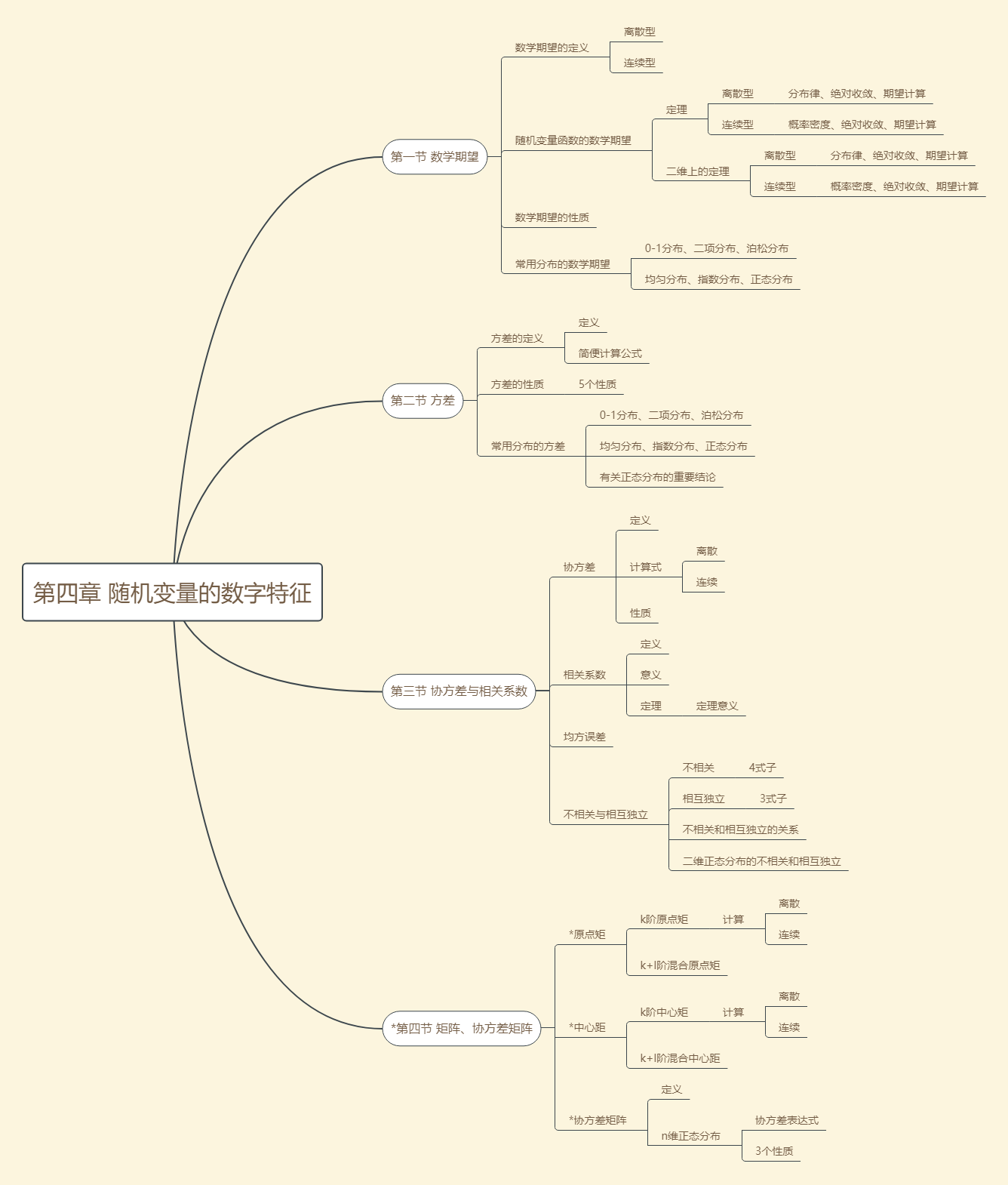
第一节 数学期望
数学期望的定义
离散型随机变量的数学期望:
设离散型随机变量\(X\)的分布律为\(P\left \{ X=x_{k} \right \}p_{k}, k=1,2,...\),若级数
\(\sum_{k=1}^{\infty}x_{k}p_{k}\)
绝对收敛,则称该级数的和为随机变量\(X\)的数学期望,记为\(E(X)\),即
\(E(X)=\sum_{k=1}^{\infty}x_{k}p_{k}\)
连续型随机变量的数学期望:
设连续型随机变量\(X\)的概率密度为\(f(x)\),若积分
\(\int_{-\infty}^{+\infty}xf(x)dx\)
绝对收敛,则称该积分的值为随机变量\(X\)的数学期望,记为\(E(X)\),即
\(E(X)=\int_{-\infty}^{+\infty}xf(x)dx\)
随机变量函数的数学期望
定理:
设\(Y\)是随机变量\(X\)的函数\(P\left \{ X=x_{i},Y=y_{i} \right \}=p_{ij}(i,j = 1,2,...)\)(\(g\)是连续函数)
- \(X\)是离散型随机变量:
分布律为\(P\left \{ X=x_{i} \right \}=p_{k},k=1,2,...\)
若\(\sum_{k=1}^{\infty}g(x_{k})p_{k}\)绝对收敛,则有
\(E(Y)=E[g(X)]=\sum_{k=1}^{\infty}g(x_{k})p_{k}\) - \(X\)是连续型随机变量:
概率密度为\(f(x)\)
若\(\int_{-\infty}^{+\infty}g(x)f(x)dx\)绝对收敛,则有
\(E(Y)=E[g(X)]=\int_{-\infty}^{+\infty}g(x)f(x)dx\)
推广到二维随机变量的定理:
- \((X,Y)\)是二维离散型随机变量:
分布律为\(P\left \{ X=x_{i},Y=y_{i} \right \}=p_{ij}(i,j=1,2,...)\)
若\(\sum_{i}\sum_{j}g(x_{i},y_{i})p_{ij}\)绝对收敛,则有
\(E(Z)=E[g(X,Y)]=\sum_{i}\sum_{j}g(x_{i},y_{i})p_{ij}\) - \((X,Y)\)是二维连续型随机变量:
概率密度为\(f(x,y)\)
若\(\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)\cdot f(x,y)dxdy\)绝对收敛,则有
\(E(Z)=E[g(X,Y)]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)\cdot f(x,y)dxdy\)
数学期望的性质
设随机变量\(X,Y\)的数学期望\(E(X),E(Y)\)存在,则
- \(E(c)=c\)其中\(c\)是常数
- \(E(cX)=cE(X)\)
- \(E(X+Y)=E(X)+E(Y)\)
- 若\(X,Y\)是相互独立的,则有\(E(XY)=E(X)E(Y)\)
常用分布的数学期望
0-1分布:\(E(X)=p\)
二项分布:\(E(X)=np\)
泊松分布:\(E(X)=\lambda\)
均匀分布:\(E(X)=\frac{a+b}{2}\)
指数分布:\(E(X)=\frac{1}{\lambda }\)
正态分布:\(E(X)=\mu\)
第二节 方差
方差的定义
定义:
设\(X\)是一个随机变量,若
\(E[X-E(X)]^{2}\)存在,
则称\(E[X-E(X)]^{2}\)为\(X\)的方差,记为\(D(X)\),即
\(D(X)=E[X-E(X)]^{2}\)
称\(\sqrt{D(X)}\)为随机变量\(X\)的标准差或均方差,记为\(\sigma (X)\)
(方差是随机变量\(X\)的函数\(g(X)=[X-E(X)]^{2}\)的数学期望)
计算方差的简便公式:\(D(X)=E(X^{2})-[E(X)]^{2}\)
(能看出随机变量\(X\)和其自身不相互独立)
方差的性质
定理:
设随机变量\(X\)与\(Y\)的方差存在,则
- 设\(c\)为常数,则\(D(c)=0\)
- 设\(c\)为常数,则\(D(cX)=c^{2}D(X)\)
- \(D(X\pm Y)=D(X)+D(Y)\pm 2E[(X-E(X))(Y-E(Y))]\)
- 若\(X,Y\)相互独立,则\(D(X\pm Y)=D(X)+D(Y)\)
- 对任意的常数\(c\neq E(X)\),有\(D(X)<E[(X-c)^{2}]\)
常用分布的方差
- (0-1)分布:\(D(X)=p(1-p)\)
- 二项分布:\(D(X)=np(1-p)\)
- 泊松分布:\(D(X)=\lambda\)
- 均匀分布:\(D(X)=\frac{(b-a)^{2}}{12}\)
- 指数分布:\(D(X)=\frac{1}{\lambda ^{2}}\)
- 正态分布:\(D(X)=\sigma ^{2}\)
重要结论:
\(\mu\)和\(\sigma\)分别是正太分布的数学期望和均方差,根据这一性质有:
\(c_{1}X_{1}+c_{2}X_{2}+...+c_{n}X_{n}\sim N(\sum_{i=1}^{n}c_{i}\mu _{i},\sum_{i=1}^{n}c_{i}^{2}\sigma _{i}^{2})\)
(\(X_{1},X{2},...,X_{n}\)相互独立)
第三节 协方差与相关系数
协方差:
- 定义:\(cov(X,Y)=E\left \{ [X-E(x)][Y-E(Y)] \right \}\)
(称\(cov(X,Y)\)为二维随机变量\(X,Y\)的协方差) - 计算式:\(cov(X,Y)=E(XY)-E(X)E(Y)\)
离散型:\(cov(X,Y)=\sum_{i}\sum_{j}[x_{i}-E(X)][y_{i}-E(Y)]p_{ij}\)
连续型:\(cov(X,Y)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}[x-E(X)][y-E(Y)]f(x,y)dxdy\) - 性质:
1):若X与Y独立,则\(cov(X,Y)=0\)
2):\(cov(X,Y)=cov(Y,X)\)
3):\(cov(aX,bY)=abcov(X,Y)\)
4):\(cov(X_{1}+X_{2},Y)=cov(X_{1},Y)+cov(X_{2},Y)\)
相关系数:
- 定义:\(\rho _{XY}=\frac{cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\)
(称\(\rho _{XY}\)为二维随机变量\(X,Y\)的相关系数或标准协方差) - 意义:\(\rho _{XY}=\frac{cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}=\frac{E\left \{ [X-E(x)][Y-E(Y)] \right \}}{\sqrt{D(X)}\sqrt{D(Y)}}=E\left \{ \frac{[X-E(x)]}{\sqrt{D(X)}}\frac{[Y-E(Y)]}{\sqrt{D(Y)}} \right \}=E(X^{*}Y^{*})\)
其中\(X^{*}\)和\(Y^{*}\)分别是\(X\)和\(Y\)的标准化随机变量,它们均是期望为0方差为1的随机变量,所以也有
\(cov(X^{*},Y^{*})=\rho _{X^{*}Y^{*}}=E(X^{*}Y^{*})\) - 定理:(具体推导思路是利用最小二乘法)
设\(D(X)>0,D(Y)>0\),\(\rho _{XY}\)为\((X,Y)\)的相关系数,则
1):若\(X,Y\)相互独立,则\(\rho _{XY}=0\)
2):\(\left | \rho _{XY} \right |\leq 1\)
3):\(\left | \rho _{XY} \right |= 1\)的充要条件是存在常数\(a,b\),使
\(p\left \{ Y=aX+b \right \}=1, a\neq 0\)
其中\(a=\frac{cov(X,Y)}{D(X)}, b=E(Y)-\frac{E(X)cov(X,Y)}{D(X)}\)
(该定理说明:相关系数描述了随机变量X,Y的线性相关程度,为1时严格符合线性相关,为0时均方误差达到最大值)
均方误差:\(e=\left \{ [Y-(ax+b)]^{2} \right \}\)(刻画线性拟合的近似程度)
X和Y不相关:
- \(E(XY)=E(X)E(Y)\)
- \(D(X\pm Y)=D(X)+D(Y)\)
- \(cov(X,Y)=0\)
- \(\rho _{XY}=0\)
X和Y相互独立
- \(f(x,y)=f_{X}(x)f_{Y}(y)\)
- \(P_{ij}=P_{i\cdot }P_{\cdot j}\)
- \(F(x,y)=F_{X}(x)F_{Y}(y)\)
X和Y不相关与X和Y相互独立:
- 相互独立是不相关的充分不必要条件
- 在二维正态随机变量X,Y下,不相关等价于相互独立
\(cov(X,Y)=\rho \sigma _{1}\sigma _{2}\)的证明可以看出
*第四节 矩阵、协方差矩阵
原点矩:
- \(E(X^{k}), k=1,2,...\):X的k阶原点矩,简称k阶矩
- \(E(X^{k}Y^{l}), k=1,2,...\):X和Y的k+l阶混合原点矩
- 计算:
离散型:\(E(X^{k})=\sum_{i=1}^{\infty}x_{i}^{k}p_{i}\)
连续型:\(E(X^{k})=\int_{-\infty}^{+\infty}x^{k}f(x)dx\)
中心距:
- \(E[X-E(X)]^{k}, k=1,2,...\):X的k阶中心距
- \(E[X-E(X)]^{k}[Y-E(Y)]^{l}, k=1,2,...\):X和Y的k+k阶混合中心距
离散型:\(E[X-E(X)]^{k}=\sum_{i=1}^{\infty}[X-E(X)]^{k}p_{i}\)
连续型:\(E[X-E(X)]^{k}=\int_{-\infty}^{+\infty}[X-E(X)]^{k}f(x)dx\)
协方差矩阵:
设n维随机变量\((X_{1},X_{2},...,X_{n})\)的1+1阶混合中心距
\(\sigma _{ij}=cov(X_{i},X_{j})=E\left \{ [X_{i}-E(X_{i})][X_{j}-E(X_{j})] \right \}, i,j=1,2,...,n\)
都存在,则称矩阵
\(\Sigma =\begin{pmatrix}\sigma _{11} & \sigma _{12} & ... & \sigma _{1n}\\ \sigma _{21} & \sigma _{22} & ... & \sigma _{2n}\\ ... & ... & & ...\\ \sigma _{n1} & \sigma _{n2} & ... & \sigma _{nn}\end{pmatrix}\)
为n维随机变量\((X_{1},X_{2},...,X_{n})\)的协方差矩阵
(不难看出协方差矩阵是对称矩阵)
n维正态随机变量\((X_{1},X_{2},...,X_{n})\)的概率密度:
\(f(x_{1},x_{2},...,x_{n})=\frac{1}{(2\pi )^{\frac{n}{2}}\sqrt{|\Sigma|}}exp\left \{ -\frac{1}{2}(X-\mu)^{T}\Sigma ^{-1}(X-\mu) \right \}\)
其中\(\Sigma\)是\((X_{1},X_{2},...,X_{n})\)的协方差矩阵
n维正态随机变量\((X_{1},X_{2},...,X_{n})\)的性质:
- n维正态随机变量\((X_{1},X_{2},...,X_{n})\)服从n维正态分布的充要条件是\((X_{1},X_{2},...,X_{n})\)的任意线性组合
\(l_{1}X_{1}+l_{2}X_{2}+...+l_{n}X_{n}\)
服从一维正态分布,其中\(l_{1},l_{2},...,l_{n}\)不全为0 - 若\((X_{1},X_{2},...,X_{n})\)服从n维正态分布,设\((Y_{1},Y_{2},...,Y_{n})\)是\((X_{1},X_{2},...,X_{n})\)的线性函数,则\((Y_{1},Y_{2},...,Y_{n})\)服从k维正态分布
- 设\((X_{1},X_{2},...,X_{n})\)服从n维正态分布,则\((X_{1},X_{2},...,X_{n})\)相互独立的充要条件是\((X_{1},X_{2},...,X_{n})\)两两不相关


 浙公网安备 33010602011771号
浙公网安备 33010602011771号