数据库系统概论笔记（6）

第6章关系数据理论

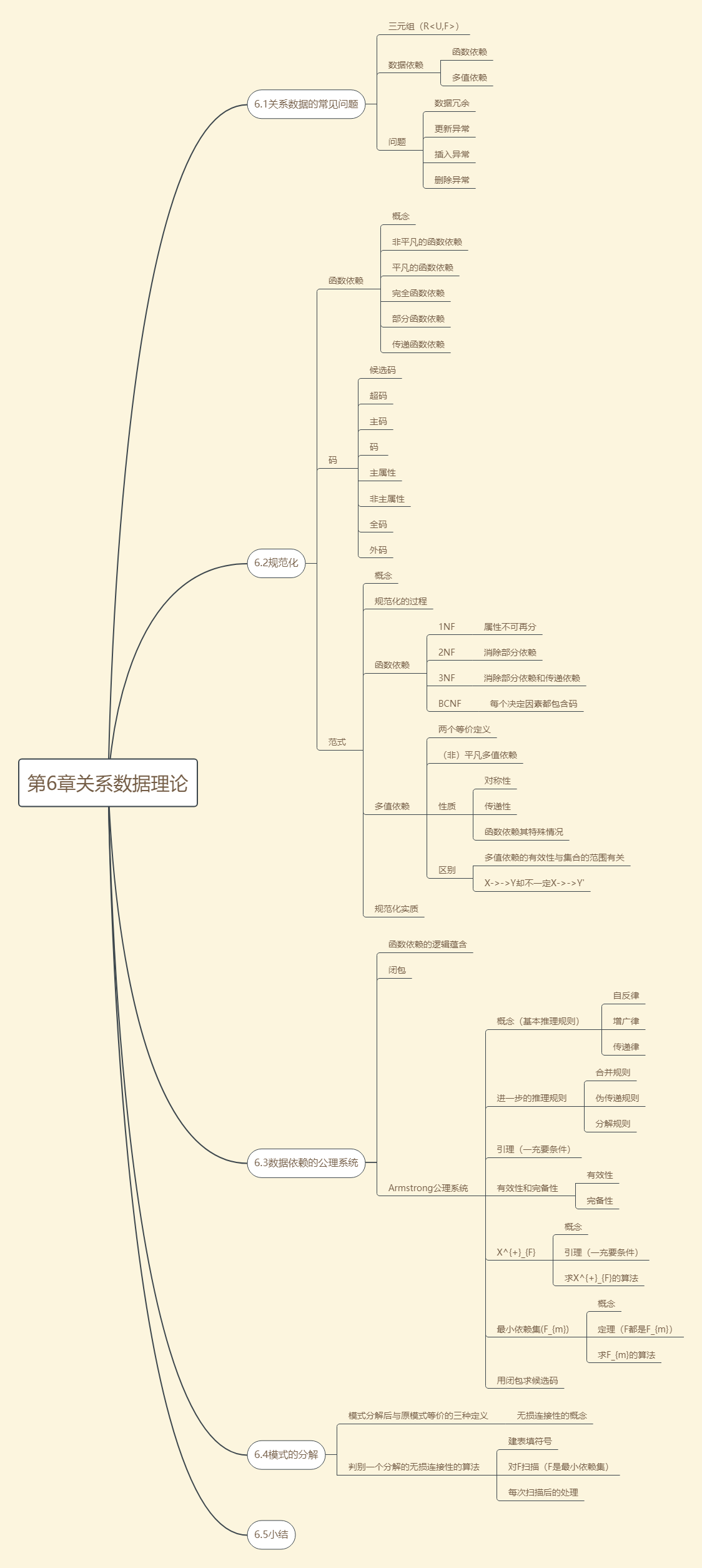
6.1问题的提出

关系数据库应当是一个五元组R(U,D,DOM,F)

关系名R是符号化的元组语义
U为一组属性
D为属性组U中的属性所来自的域
DOM为属性到域的映射
F为属性组U上的一组数据依赖

在设计模式中，D、DOM与模式设计关系不大，此时可以看作一个三元组：R<U,F>
当且仅当U上关系r满足F时，r称为关系模式R<U,F>的一个关系
第一范式：每个分量是不可分的数据项

数据依赖：一个关系内部属性与属性之间的一种约束关系（此约束关系通过属性间值的相等与否来体现）

特点：是现实世界属性间相互联系的抽象，是数据内在的性质，是语义的体现
两种重要的数据依赖：函数依赖、多值依赖
函数依赖：类似于数学的函数y=f(x)，自变量x确定后y也唯一确定（Sname=f(Sno)记作Sno->Sname）

建立一个学校教务系统的数据库
Student<U,F>
U={Sno,Sdept,Mname,Cno,Grade}
F={Sno->Sdept,Sdept->Mname,(Sno,Cno)->Grade}

此关系模式存在的问题（好模式要避免的问题）：

数据冗余
（比如Manme重复出现）
更新异常
（比如更换系主任后，必须修改所有相关的Mname）
插入异常
（比如刚建表时不能插入只含Mname的元组）
删除异常
（比如所有学生毕业删除所有元组，Mname信息也丢失了）

解决方法：用规范化理论消除不好的数据依赖

6.2规范化

函数依赖

函数依赖的定义：对R(U)的任一关系r,不可能存在两个元组在X上的属性值相等，而Y上的属性值不等，则称X函数确定Y或Y函数依赖于X（记作X->Y）
（注意：函数依赖和别的数据依赖一样是语义范畴的概念，只能根据语义来确定一个函数依赖，而且函数依赖要求R的一切关系均要满足约束条件）

非平凡的函数依赖
X->Y，但Y $\nsubseteq$ X
平凡的函数依赖
X->Y，但Y $\subseteq$ X
决定因素
X->Y中的X
X<-->Y
X->Y且Y->X
X-/->Y
Y不函数依赖于X

完全函数依赖：在R(U)中，如果X->Y，并且对于X的任何一个真子集X'，都有X'-/->Y，则称Y完全函数依赖于X（记作X $\overset{F}{\rightarrow}$ Y）
部分函数依赖：X->Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖（记作X $\overset{P}{\rightarrow}$ Y）
传递函数依赖：在R(U)中，如果X->Y(Y $\nsubseteq$ )，Y-/->X，Y->Z，Z $\nsubseteq$ Y，则称Z对X传递函数依赖（记作X $\overset{传递}{\rightarrow}$ Y）

码

候选码：设K为R<U,F>中的属性或属性组合，若K $\overset{F}{\rightarrow}$ U，则K为R的候选码
超码：U部分函数依赖于K（K->U），则称K为超码
主码：选定其中一个候选码为主码
码：候选码或主码的简称

主属性：包含在任何一个候选码中的属性
非主属性：不包含在任何候选码中的属性
全码：整个属性都是码
外码：关系模式R中属性或属性组X并非R的码，但X是另一个关系模式的码，则称X是R的外码

范式

概念：关系数据库中满足不同程度要求的关系
规范化：低级范式的关系模式通过模式分解，转换成若干个高级的关系模式的过程

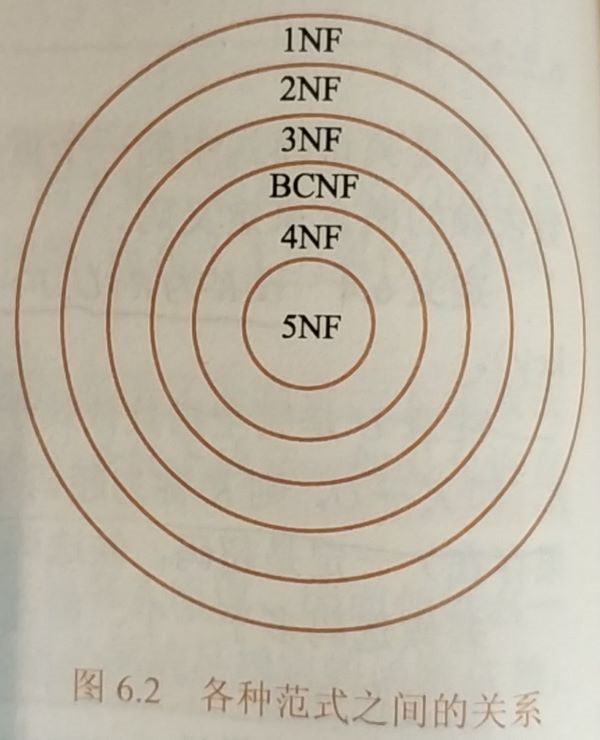
1NF：符合1NF的关系中的每个属性都不可再分
2NF：R $\in$ 1NF，且每一个非主属性完全函数依赖于任何一个候选码，则R $\in$ 2NF（消除所有非主属性对任意一个候选码的部分依赖）

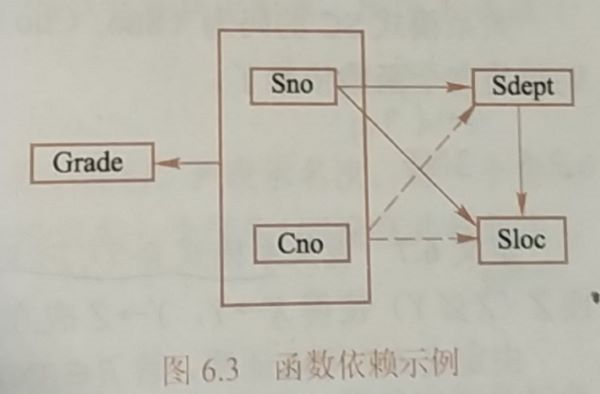
（转换前1NF）

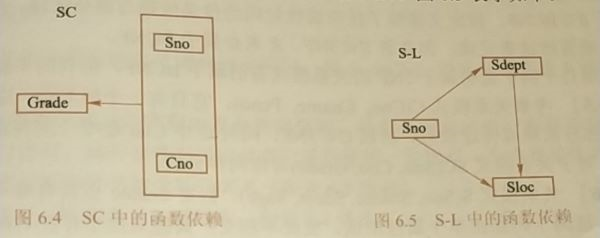
（转换后2NF）
3NF：设关系模式R<U,F> $\in$ 1NF，若R中不存在这样的码X，属性组Y及非主属性Z（Z $\nsubseteq$ Y），使得X->Y，Y->Z成立，Y-/->X，则称R<U,F> $\in$ 3NF（消除非主属性对码的部分依赖和传递依赖）
BCNF（扩充的第三范式）：关系模式R<U,F> $\in$ 1NF，若X->Y且Y $\nsubseteq$ X时X必含有码，则R<U,F> $\in$ BCNF（每一个决定因素都包含码）
满足3NF，但不满足BCNF的例子：

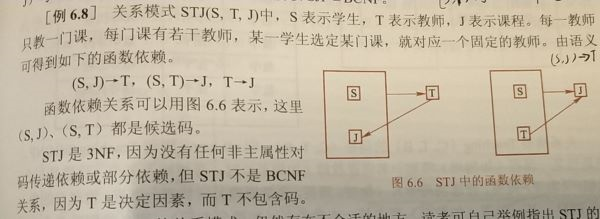
多值依赖

定义：
设R(U)是属性集U上的一个关系模式。
X,Y,Z是U的子集，并且Z=U-X-Y。
关系模式R(U)中多值依赖X->->Y成立，当且仅当对R(U)的任一关系r，给定的一对(x,z)值，有一组Y的值，这组值仅仅决定于x值而与z值无关（一个X的值确定一组Y的值（一对多））

另一等价形式的定义：
在R(U)的任一关系r中，如果存在元组t、s使得t[X]=s[X]，那么就必然存在元组w、v∈r（w、v可以与s、t相同），使得w[X]=v[X]=t[X]
而w[Y]=t[Y]，w[Z]=s[Z]，v[Y]=s[Y]，v[Z]=t[Z]（即交换s、t元组的Y值所得的两个新元组必在r中）
则Y多值依赖于X，记为X->->Y

平凡的多值依赖：
若x->->Y，而Z= $\phi$ ，即Z为空，则称X->->Y为平凡的多值依赖，否则为非平凡的多值依赖（实际多讨论非平凡）
（即对于R(X,Y)，若有X->->Y成立，则X->->Y为平凡的多值依赖）

多值依赖的性质：

多值依赖具有对称性
若X->->Y，则X->->Z，其中Z=U-X-Y
多值依赖具有传递性
若X->->Y，Y->->Z，则X->->Z-Y
函数依赖可以看做是多值依赖的特殊情况
若X->Y，则X->->Y
若X->->Y，X->->Z，则
X->->YZ
X->->Y∩Z
X->->Y-Z，X->->Z-Y

多值依赖与函数依赖的区别：

多值依赖的有效性与集合的范围有关
若X->->Y在U上成立，则X->->Y在W（W $\subseteq$ U）上也成立，反之则不一定
若函数依赖X->Y在R(U)上成立，则对于任何Y' $\subset$ Y，均有X->Y'成立
而多值依赖X->->Y在R(U)上成立，却不能断言对于任何Y' $\subset$ Y有X->->Y'成立

多值依赖的缺点：数据冗余太大

4NF

定义：关系模式R<U,F>∈1NF，若对于R的每个非平凡多值依赖X->->Y（Y $\nsubseteq$ X），X都有码，则称R<U,F>∈4NF
（4NF就是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖）

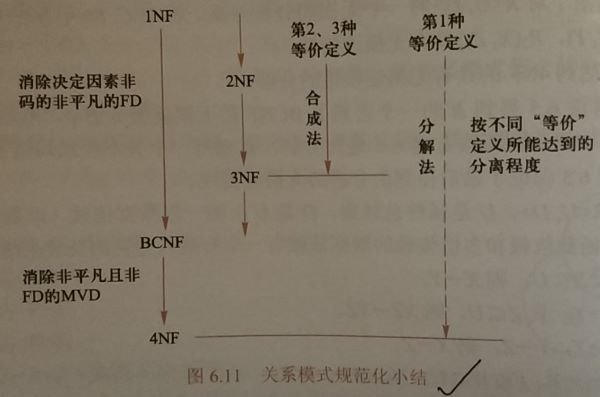
小结

规范化的基本思路：逐步消除数据依赖中不合适的部分，使模式中的各关系模式达到某种程度的分离（规范化是实质是概念的单一化）

6.3数据依赖的公理系统

函数依赖的逻辑蕴涵定义：对于满足一组函数依赖F的关系模式R<U,F>，其任何一个关系r，若函数依赖X->Y都成立（即r中任意两元组t、s，若t[X]=s[X]，则t[Y]=s[Y]），则称F逻辑蕴含X->Y（X->Y不一定在F中，但F能推出X->Y）
闭包的定义：在关系模式R<U,F>中为F所逻辑蕴含的函数依赖的全体叫做F的闭包，记为 $F^{+}$

Armstrong公理系统：
设U为属性集总体，F是U上的一组函数依赖，于是有关系模式R<U,E>满足以下的推理规则：

自反律
若Y $\subseteq$ X $\subseteq$ U，则X->Y为F所蕴含
（由自反律所得到的函数依赖均是平凡的函数依赖，自反律的使用不依赖于F）
增广律
若X->Y为F所蕴含，且Z $\subseteq$ U，则XZ->YZ为F所蕴含
传递律
若X->Y及Y->Z为F所蕴含，则X->Z为F所蕴含

由Armstrong进一步得到的推理规则

合并规则
由X->Y，X->Z，有X->YZ
伪传递规则
由X->Y，WY->Z，有XW->Z
分解规则
由X->Y及Z $\subseteq$ Y，有X->Z

引理： $X->A_{1}A_{2}...A_{k}$ 成立的充分必要条件是 $X->A_{i}$ 成立（i=1,2,...,k）

Armstrong公理系统具有有效性和完备性：

有效性：由F出发根据Armstrong公理推导出来的每一个函数依赖一定在 $F^{+}$ 中
有效性（正确性）证明：略
完备性： $F^{+}$ 中的每一个函数依赖，必定可以由F出发根据Armstrong公理推导出来
完备性证明：略
（完备性能说明：F的“导出”和“蕴含”是两个完全等价的概念， $F^{+}$ 可以说成是F出发借助Armstrong导出的函数依赖的集合）

$X_{F}^{+}$ 定义：设F为属性集U上的一组函数依赖，X、Y $\subseteq$ U， $X_{F}^{+}$ ={A|X->A能由F根据Armstrong公理系统导出}， $X_{F}^{+}$ 称为属性集X关于函数依赖集F的闭包
引理：设F为属性集U上的一组函数依赖，X、Y $\subseteq$ U，X->Y能由F根据Armstrong公理导出的充要条件是Y $\subseteq X_{F}^{+}$
求 $X_{F}^{+}$ 的算法（步骤）：

令 $X^{(0)}=X, i=0$
求B，其中 $B=\left \{ A|(\exists V)(\exists W)(V\rightarrow W\in F\wedge V\subseteq X^{(i)}\wedge A\in W) \right \}$
$X^{(i+1)}=B\cup X^{(i)}$
判断 $X^{(i+1)}=X^{(i)}$
若 $X^{(i+1)}=X^{(i)}$ 或 $X^{(i)}=U$ ，则 $X^{(i)}$ 就是 $X_{F}^{+}$ ，结束算法
$i=i+1$ 返回第2步
（可以看出该算法最多执行 $|U|-|X|$ 次）

函数依赖集等价：若 $F^{+}=G^{+}$ ，就说函数依赖集F覆盖G（或G覆盖F）或F与G等价
引理： $F^{+}=G^{+}$ 的充要条件是 $F\subseteq G^{+}$ 和 $G\subseteq F^{+}$
（对于 $F\subseteq G^{+}$ ，只需逐一对F中的函数依赖X->Y考察Y是否属于 $X^{+}_{G^{+}}$ 即可）

最小依赖集（最小覆盖）：
满足以下三个条件（求最小依赖集的过程）：

F中任一函数依赖的右部仅含有一个属性（右部单一属性化）
F中不存在这样的函数依赖X->A，X有真子集Z使得(F-{X->A})∪{Z->A}与F等价（去除部分依赖变为完全依赖）
F中不存在这样的函数依赖X->A，使得F与F-{X->A}等价（消除冗余的依赖）
方法：逐一去除依赖（X->Y），再用闭包运算看影不影响（去除后 $X^{+}_{F}$ 还包不包含Y）

定理：每一个函数依赖集F均等价于一个最小依赖集 $F_{m}$ ，此 $F_{m}$ 称为F的最小依赖集（最小依赖集可能不唯一）
（证明的实质是求解最小依赖集的过程）

用闭包求候选码：

求关系模式R<U,F>的最小函数依赖集F
分别计算出UL,UR,UB
UL：仅在函数依赖集中各依赖关系式左边出现的属性的集合
UR：仅在函数依赖集中各依赖关系式右边出现的属性的集合
UB = U - UL - UR
若 $UL=\phi$ ,转第5步
计算 $UL$ 的闭包
若 $UL^{+}=U$ ，则 $UL$ 为 $R$ 的唯一的候选码，算法结束
若 $UL^{+}\neq U$ ，转第4步
将UL依次与UB中的属性组合，利用定义（闭包运算）判断该组合属性是否是候选码，找出所有的候选码后算法结束
对UB中的属性及属性组合利用定义（闭包运算）依次进行判断，找出所有的候选码后算法结束

https://wonzwang.blog.csdn.net/article/details/80464679

6.4模式的分解

* $m_{\rho }(r)$ 的定义：
设 $\rho = \left \{ R_{1}<U_{1},F_{1}>,...,R_{k}<U_{k},F_{k}> \right \}$ 是R<U,F>的一个分解，r是R<U,F>的一个关系。
定义 $m_{\rho }(r)=\bowtie ^{k}_{i=1}\pi _{R_{i}}(r)$ ，即 $m_{\rho }(r)$ 是r在 $\rho$ 中各关系模式上投影的连接，而 $\pi _{R_{i}}(r)=\left \{ t.U_{i}|t\in r \right \}$

*无损分解的定义：
$\rho = \left \{ R_{1}<U_{1},F_{1}>,...,R_{k}<U_{k},F_{k}> \right \}$ 是R<U,F>的一个分解，若对R<U,F>的任何一个关系r均有 $r=m_{\rho }(r)$ 成立，则称分解 $\rho$ 具有无损连接性，简称 $\rho$ 为无损分解

模式分解后与原模式等价的三种定义：

分解具有无损连接性（通过自然连接后属性可以还原）
分解要保持函数依赖（能还原函数依赖与原模式相同）
分解既要保持函数依赖，又要保持无损连接性

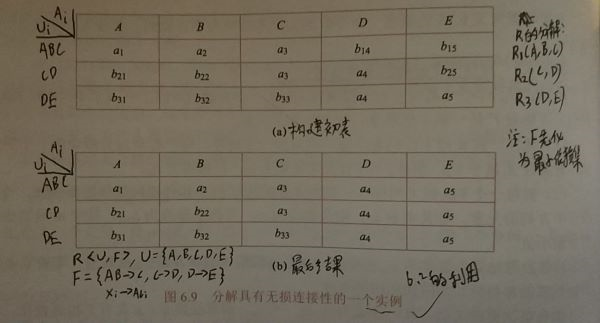
判别一个分解的无损连接性的算法：
$\rho = \left \{ R_{1}<U_{1},F_{1}>,...,R_{k}<U_{k},F_{k}> \right \}$ 是 $R<U,F>$ 的一个分解； $U=\left \{ A_{1},...,A_{n} \right \}$ ， $F=\left \{ FD_{1},FD_{2},...,FD_{\rho } \right \}$ （F是极小依赖集）

建表填符号：
建立一张n列k行的表，每一列对应一个属性，每一行对应分解中的一个关系模式，若属性 $A_{j}$ 属于 $U_{i}$ ，则在j列i行交叉处填上 $a_{j}$ ，否则填上 $b_{ij}$
对F扫描（对F中p个FD逐个处理）：
对每个 $FD_{i}$ 做出操作：找到 $X_{i}$ 所对应的列中具有相同符号的那些行，考察行中 $li$ 列的元素。若有 $a_{li}$ ，则全部改为 $a_{li}$ ；否则全部改为 $b_{mli}$ ，其中m是这些行的行号最小值
若某个 $b_{tli}$ 被更改，那么该表的 $li$ 列中凡是 $b_{tli}$ 的符号（不管它是否是开始找到的那些行）均应做相应的更改
某次扫描后，若
表无变化：算法终止，分解 $\rho$ 不具有无损连接性
有一行成为 $a_{1},a_{2},...,a_{n}$ ：算法终止，分解 $\rho$ 具有无损连接性
其余：返回第2步进行下一个循环（每循环一次表内符号必减少，符号有限，算法有穷）