概率论笔记（3）

第三章随机向量

第一节二维随机向量及其分布

二维随机变量的定义及其分布函数

n维随机向量：
$E$是一个随机试验，其样本空间是$\Omega =\left \{ e \right \}$
设随机变量$X_{1}(e),X_{2}(e),...,X_{n}(e)$是定义在样本空间$\Omega$上的$n$个随机变量
则称向量$(X_{1}(e),X_{2}(e),...,X_{n}(e))$为$\Omega$上的$n$维随机变量（随机向量），简记为$(X_{1},X_{2},...,X_{n})$

n维随机变量的分布函数：
设$(X_{1},X_{2},...,X_{n})$是n维随机变量，对任意实数$x_{1},x_{2},...,x_{n}$，称n元函数
$F(x_{1},x_{2},...,x_{n})=P\left \{ X_{1}\leq x_{1},X_{2}\leq x_{2},...,X_{n}\leq x_{n} \right \}$为n维随机变量$(X_{1},X_{2},...,X_{n})$的联合分布函数
分布函数$F(x,y)$的性质：

1. $F(x,y)$是变量$x$和$y$的不减函数
2. $0\leq F(x,y)\leq 1$，且$F(-\infty ,y)=0$（$y$固定），且$F(x,-\infty)=0$（$x$固定）,$F(-\infty,-\infty)=0,F(+\infty,+\infty)=1$
3. $F(x,y)$关于$x$和$y$是右连续的，即$F(x,y)=F(x+0,y),F(x,y)=F(x,y+0)$
4. 对于任意$(x_{1},y_{1}),(x_{2},y_{2}),x_{1}<x_{2},y_{1}<y_{2}$。有$F(x_{2},y_{2})-F(x_{2},y_{1})-F(x_{1},y_{2})+F(x_{1},y_{1})\geq 0$

二维离散型随机变量

二维离散型随机变量：若二维随机变量$(X,Y)$的所有可能结果取值是有限对或可数无穷多时，则称$(X,Y)$为二维离散型随机变量

二维离散型随机变量的分布律：$P(X=x_{i},Y=y_{i})=p_{i,j}, i,j=1,2,...$
性质：

1. 非负性：$p_{i,j}\geq 0, i,j=1,2,...$
2. 规范性：$\sum_{i,j}p_{i,j}=1$

二维离散型随机变量的分布函数：$F(x,y)=P\left \{ X\leq x,Y\leq y \right \}=\sum_{x_{i}\leq x}\sum_{y_{j}\leq y}p_{ij}$

二维连续型随机变量

二维连续型随机变量的密度函数：
设随机变量$(X,Y)$的分布函数为$F(x,y)$，若存在一个非负可积函数$f(x,y)$，使得对任意实数$x,y$有
$F(x,y)=P\left \{ X\leq x,Y\leq y \right \}=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv$
则称$(X,Y)$为二维连续型随机变量，称$f(x,y)$为$(X,Y)$的联合分布密度或概率密度
性质：

1. $f(x,y)\geq 0, -\infty <x,y<+\infty$
2. $\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(u,v)dudv=1$
3. 若$f(x,y)$在点$(x,y)$处连续，则有$\frac{\partial ^{2}F(x,y)}{\partial x\partial y}=f(x,y)$
4. 设$G$为$xOy$平面上的任一区域，随机点$(X,Y)$落在$G$内的概率为$P\left \{ (X,Y)\in G \right \}=\iint_{G}f(x,y)dxdy.$

3维随机变量的均匀分布：
$G$为空间上的有界区域，体积为$A$，若三维随机变量$(X,Y,Z)$在$G$上具有概率密度
$f(x,y)=\left\{\begin{matrix}\frac{1}{A}, & (x,y,z)\in G\\ 0, & 其它\end{matrix}\right.$
则称$(X,Y,Z)$在$G$上服从均匀分布
（类似可拓展至n维随机变量的均匀分布）

二维随机变量$(X,Y)$的二维正太分布:

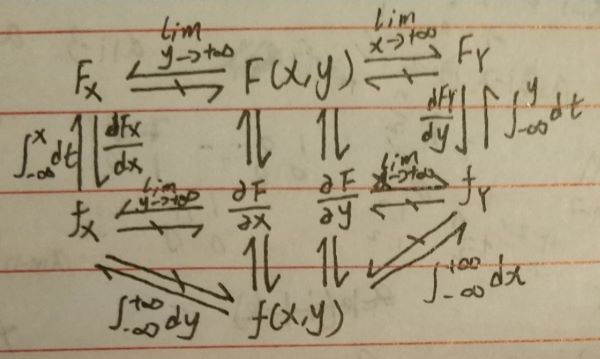
第二节边缘分布

定义：二维随机变量$(X,Y)$中$X,Y$各自的分布函数$F_{x},F_{y}$
其中$F_{x}=F(x,+\infty ), F_{y}=F(+\infty ,y)$

二维离散型随机变量的边缘分布

二维离散型随机变量$(X,Y)$的分布律为$P\left \{ X=x_{i},Y=y_{i} \right \}=P_{ij}, i,j=1,2,...$
则有边缘分布函数$F_{X}(x)=F(x,+\infty )=\sum_{x_{i}\leq x}\sum_{j}p_{ij}$
则X的分布律为$P\left \{ X=x_{i} \right \}=\sum_{j}p_{ij},i=1,2,...$ 也可写作$p_{i\cdot }$
（称其为$(X,Y)$关于X的边缘分布律，Y同理）

二维连续型随机变量的边缘分布

二维连续型随机变量$(X,Y)$的概率密度为$f(x,y)$
则X的分布函数为$F_{X}(x)=F(x,+\infty)$
则X的概率密度为$f_{X}(x)=\frac{dF_{X}(x)}{dx}=\int_{-\infty }^{+\infty }f(x,y)dy$
（称其为$(X,Y)$关于X的边缘密度函数，Y同理）
（Y同理）

求边缘概率密度技巧：运算、对象

• 运算：
  给定联合分布函数：求极限（忘了是啥，极限操作是求边缘分布函数用的，应该先用此求边缘分布函数，再求导得出边缘概率密度，这一条不能用对象那栏的原则）
  给定联合密度函数：求积分
  给定边缘分布函数：求导
• 对象：
  求关于X的：对Y作运算
  求关于Y的：对X作运算
  

第三节条件分布

二维离散型随机变量的条件分布律

定义：设$(X,Y)$是二维离散型随机变量，对于固定的j，若$P\left \{ Y=y_{j} \right \}>0$，则称
$P\left \{ X=x_{i}|Y=y_{j} \right \}=\frac{P\left \{ X=x_{i},Y=y_{j} \right \}}{P\left \{ Y=y_{j} \right \}}, i=1,2,...$
为在$Y=y_{i}$条件下随机变量X的条件分布律
（Y同理）

二维连续型随机变量的条件分布

定义：设对于任何固定的正数$\varepsilon$，$P\left \{ y-\varepsilon <Y\leq y+\varepsilon \right \}>0$，若
$\lim_{\varepsilon \rightarrow 0^{+}}P\left \{ X\leq x | y-\varepsilon <Y\leq y+\varepsilon \right \}=\lim_{\varepsilon \rightarrow 0^{+}}\frac{P\left \{ X\leq x , y-\varepsilon <Y\leq y+\varepsilon \right \}}{P\left \{ y-\varepsilon <Y\leq y+\varepsilon \right \}}$
存在，则称此极限为在$Y=y$的条件下$X$的条件分布函数，记作
$P\left \{ X\leq x | Y=y \right \}$或$F_{X|Y}(x | y)$

若$f(x,y)$和$F_{Y}(y)$连续，且$F_{Y}(y) > 0$，则在$Y=y$的条件下
$X$的条件分布函数为
$F_{X|Y}(x|y)=\int_{-\infty }^{x}\frac{f(u,y)}{f_{Y}(y)}du$
$X$的条件分布密度为
$f_{X|Y}(x | y)=\frac{f(x,y)}{f_{Y}(y)}$
（反过来对Y也类似）

第四节随机变量的独立性

定义：设$X$和$Y$为两个随机变量，若对于任意的$x$和$y$，有
$P\left \{ X\leq x,Y\leq y \right \}=P\left \{ X\leq x \right \}P\left \{ Y\leq y \right \}$
则称$X$和$Y$是相互独立的
即$F(x,y)=F_{X}(x)F_{Y}(y)$

n维随机向量的独立性：
联合分布函数=各边缘分布函数的乘积

对于二维离散型随机变量等价形式为：
$P\left \{ X=x_{i},Y=y_{i} \right \}=P\left \{ X=x_{i} \right \}P\left \{ Y=y_{i} \right \}$
（$(x_{i},y_{j})$取$(X,Y)$的任何可能值）

对于二维连续型随机变量等价形式为：
$f(x,y)=f_{X}(x)f_{Y}(y)$
（$x,y$任意）

第五节 两个随机变量函数的分布

任务：已知二维随机变量$(X,Y)$的分布律或密度函数，求$Z=\varphi (X,Y)$的分布律或密度函数
注意点：$Z=g(X,Y)$，$(X,Y)$是二维的离散型随机变量，而$Z$是一维的离散型随机变量

二维离散型随机变量函数的分布

一般计算：把Z分解成X和Y=g(X,Z)的形式，再对X、Y各种可能的取值情况相乘再求和
（例：$P\left \{ Z=k \right \}=P\left \{ X+Y=k \right \}=\sum_{i=0}^{k}P\left \{ X=i \right \}P\left \{ Y=k-i \right \}$）

分布的可加性（某些离散型随机变量具有的特性）：
若$X,Y$独立，且$X\sim P(\lambda _{1}), Y\sim P(\lambda _{2})$
则$X+Y\sim P(\lambda _{1}+\lambda _{2})$
（泊松分布、二项分布均具有分布可加性）

二维连续型随机变量函数的分布

求$f_{Z}(z)$的一般方法：

1. 先求$Z=\varphi (X,Y)$的分布函数：
   $F_{Z}(z)=P\left \{ Z\leq z \right \}=P\left \{ \varphi (X,Y)\leq z \right \}=P\left \{ (X,Y)\in G \right \}=\iint_{G}f(u,v)dudv$
   其中$G=\left \{ (x,y) | \varphi (x,y)\leq z \right \}$
2. 求出密度函数$f_{Z}(z)$:
   对分布函数进行求导

$Z=X+Y$中$Z$的概率密度：

$f_{Z}(z)=\int_{-\infty}^{+\infty}f(z-y,y)dy=\int_{-\infty}^{+\infty}f(z-x,x)dx$（$f(x,y)是联合密度函数$）
（证明思想：得出分布函数的最初积分公式后，先换元，再换积分顺序得到最终的分布函数，最后再对分布函数求导）

若$X$和$Y$独立：$f_{Z}(z)=\int_{-\infty}^{+\infty}f_{X}(z-y)f_{Y}(y)dy=\int_{-\infty}^{+\infty}f_{X}(x)f_{Y}(z-x)dx$
卷积公式：上述的公式，记为$f_{X}*f_{Y}$，即
$f_{X}*f_{Y}=\int_{-\infty}^{+\infty}f_{X}(z-y)f_{Y}(y)dy=\int_{-\infty}^{+\infty}f_{X}(x)f_{Y}(z-x)dx$
卷积：

• 具有交换律
• 两个独立随机变量的函数的分布为它们的卷积

$Z=\frac{X}{Y}$中$Z$的概率密度：

$f_{Z}(z)=\int_{-\infty}^{+\infty}f(zu,u)\left | u \right |du$（$f(x,y)是联合密度函数$）
（证明过程与$Z=X+Y$的类似）

若$X$和$Y$独立：$f_{Z}(z)=\int_{-\infty}^{+\infty}f_{X}(zu)f_{Y}(u)\left | u \right |du$

$M=max\left \{ X,Y \right \}$及$N=min\left \{ X,Y \right \}$的分布:

$F_{M}(z)=F_{X_{1}}(z)F_{X_{2}}(z)...F_{X_{n}}(z)$
$F_{N}(z)=1-[1-F_{X_{1}}(z)][1-F_{X_{2}}(z)]...[1-F_{X_{n}}(z)]$