2024迎新马拉松——字典

思路

这道题可以把每个单词正过来放在一个字典树里。

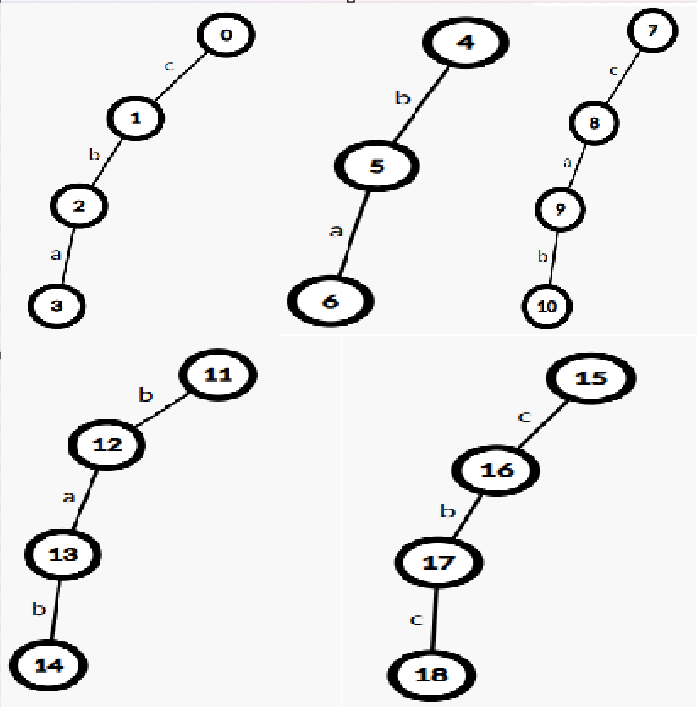
把每个单词反过来，给每个单词单独建立一个字典树。

而询问要求的就是在正串的字典树上，以前缀对应的那个节点为根的子树中，所有串的反串字典树合并之后，后缀的那个节点所对应的子树当中有多少个串就是答案。

举个小例子：

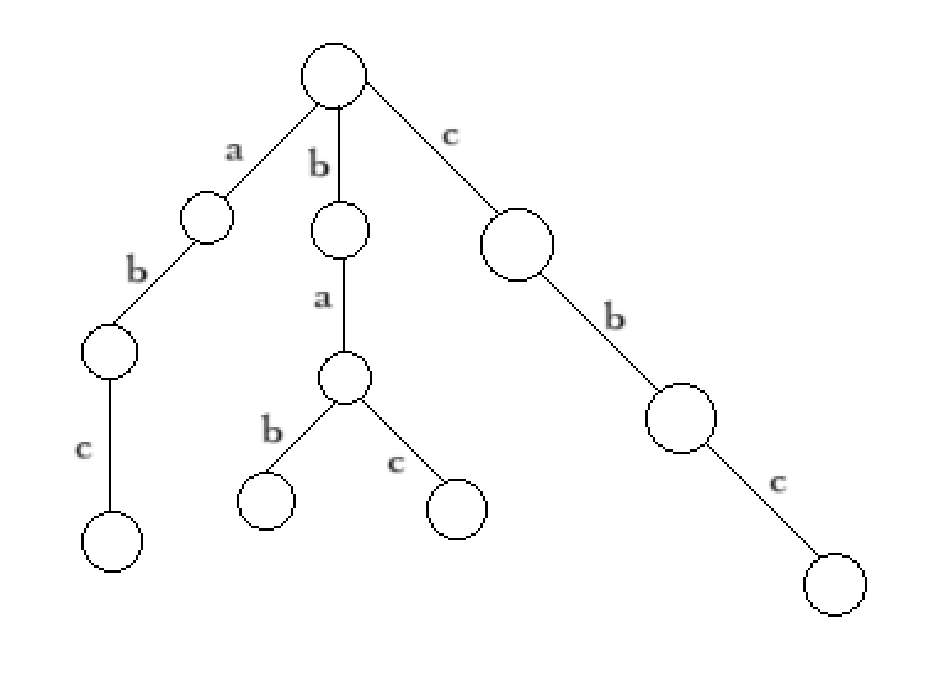
现在有 \(n\) 个单词。

分别是：“abc”，“ab”，“bac”，“bab”和“cbc”。

正串的字典树为：

反串的若干个字典树：

如果这时候要查询前缀为a，后缀为c的词有多少个，那么先去正串的字典树上找到对应的点。

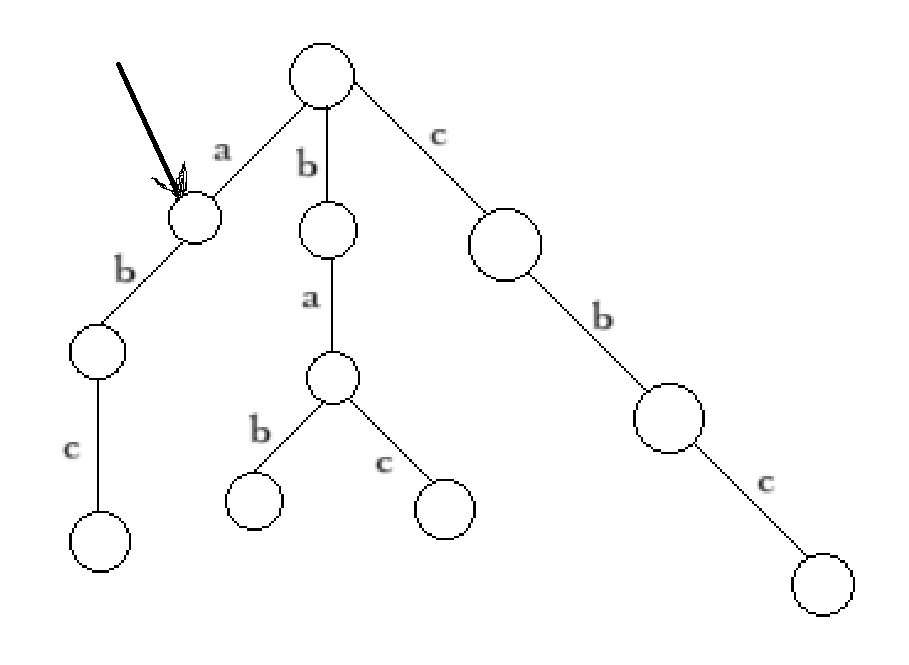
然后把他子树内反串的字典树合并。

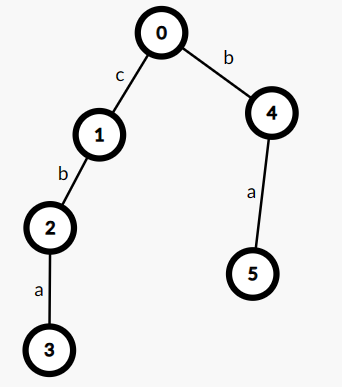
然后走后缀为c，发现他的子树中就只有一个串，答案就是 \(1\)。

核心代码：

inline ll insf(string &s) { // 给每个反串建一个字典树
	reverse(s.begin(), s.end());
	ll p = ++ftot;
	ll rt = p;
	sz[ftot] = 1;
	for (auto i : s) {
		p = ft[p][i - 'a'] = ++ftot, sz[ftot] = 1;
	}
	reverse(s.begin(), s.end());
	return rt;
}
inline ll merg(ll a, ll b) {//字典树合并
	if (!a) {
		return b;
	}
	if (!b) {
		return a;
	}
	sz[a] += sz[b];
	rep(i, 0, 25) {
		ft[a][i] = merg(ft[a][i], ft[b][i]);
	}
	return a;
}
string s[N];
struct node {
	string ht;//查询的后缀
} ask[N];
ll ans[N];
inline void addtag(string &s, ll id) {//用前缀去添加在每个节点所需要处理的询问
	ll p = 0;
	for (auto i : s) {
		ll v = i - 'a';
		if (!t[p][v]) {
			return ;
		}
		p = t[p][v];
	}
	g[p].push_back(id);
}
inline ll query(ll p, string &s) {//查询合并后的字典树，后缀为s的单词有多少个
	for (auto i : s) {
		ll v = i - 'a';
		if (!ft[p][v]) {
			return 0;
		}
		p = ft[p][v];
	}
	return sz[p];
}
ll dd[N];
inline void dfs(ll x) {//去处理每个点的询问
	if (!wei[x]) {//看当前这个点是不是一个单词
		dd[x] = ++ftot;
	} else {
		dd[x] = rt[wei[x]];
	}
	rep(i, 0, 25) {
		if (t[x][i]) {
			dfs(t[x][i]);
			merg(dd[x], dd[t[x][i]]);//把儿子的字典树和父亲的字典树合并
		}
	}
//	cout << x << " ";
	for (auto v : g[x]) {
//		cout << v << " ";
		ans[v] = query(dd[x], ask[v].ht);//处理询问
	}
//	cout << "\n";
}