范数
衡量一个向量的大小,在机器学习中,使用称为范数(norm)的函数来衡量向量大小, $L_p $范数的通用形式如下:
$||X||_p = (\sum\limits_i |x_i|^p)^\frac{1}{p} , $ 其中 $p∈R, p≥1$
当 $p=1$时, $L_1 $各个元素的绝对值之和。
$||X||_1 = \sum\limits_i |x_i| $
曼哈顿距离的正式意义为L1-距离或城市区块距离:
$d = |x_1 - x_2| + |y_1 - y_2| $
当 $p=2$时, $L_2 $被称作欧几里德范数(Euclidean norm)。它表示从原点出发到向量x确定的点的欧几里德距离。
$||X||_2 = \sqrt{ (x_1^2 + x_2^2)} $
欧几里德距离也即欧氏距离:
二维空间的公式:
$\rho = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2} , |X| = \sqrt {x_2^2 + y_2^2}$
其中, $\rho$为点$(x_2, y_2)$与点$(x_1, y_1)$之间的欧氏距离;$|X|$为点$(x_2, y_2)$到原点的欧氏距离。
三维空间的公式:
$\rho = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} , |X| = \sqrt {x_2^2 + y_2^2 + z_2^2}$
$L_2 $范数常被用来衡量向量的大小,因为它便于求导计算(如对向量中每个元素的导数只取决于对应的元素,但是它也有缺陷,即它在原点附近增长得十分缓慢),可以简单用点积$x^Tx$来计算。范数是将向量映射到非负值的函数。直观上来说,向量 x的范数就是衡量从原点到 x的距离。更严格来说,范数满足下列性质的函数:
$f(x)=0⟹x=0$
$f(x+y)≤f(x)+f(y)$
$∀α∈R,f(αx)=|α|f(x)$
当$p=1$时,称为$L_1 $范数,是向量元素绝对值之和;
当$p=0$时,上面的定义没有包含,称为0范数,定义为向量非零元素的数量
max范数(max norm):这个范数表示向量中具有最大幅度得元素的绝对值,用$L_∞ $范数表示,形式为:
$||x||_∞=max|x_i|$
两个向量的点积(dot product)也可以用范数来表示。具体地
$x^⊤y=||x||_2||y||_2cosθ$
矩阵的范数(matrix norm)
最常用的就是 F-范数(Frobenius norm),Frobenius范数,计算方式为矩阵元素的绝对值的平方和再开方。
$||A||_F = \sqrt {\sum\limits_i \sum\limits_j |a_{ij}|^2}$
设:向量$X∈R^n$,矩阵$A∈R^{n \times n}$,例如矩阵A为:
A=[2, 3, -5, -7;
4, 6, 8, -4;
6, -11, -3, 16];
(1)矩阵的1-范数,又名列模(和)范数,即矩阵列向量中绝对值之和的最大值:
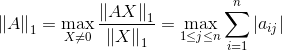
矩阵的每一列上的元素绝对值先求和,再从中取个最大的,(列和最大);上述矩阵A的1-范数为:27
(2)矩阵的2-范数,又名谱(模)范数,计算方法为$A^TA$矩阵的最大特征值的开平方:
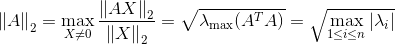
其中 $\lambda_i$为的$A^TA$特征值;矩阵的2-范数即矩阵$A^TA$的最大特征值开平方根。
简化为 $||A||_2 = \sqrt \lambda_1$,$\lambda_1$为$A^TA$的最大特征值。
(3)矩阵的无穷范数(行模):
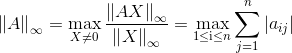
矩阵的每一行上的元素绝对值先求和,再从中取个最大的,行和最大。
补充:
欧氏距离区别于点到直接的距离
设直线 $L$ 的方程为$Ax + By + C = 0$,点$ P $的坐标为$(X_0,Y_0)$,则点$ P $到直线 $L $的距离为
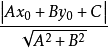



 浙公网安备 33010602011771号
浙公网安备 33010602011771号