导数放缩
导数放缩
施工中.
放缩之前:
是否对指数对数的性质熟悉?
对于每一个指数对数和 \(x\) 组合出来的函数, 按顺序考虑如下问题:
- 定义域?
- 有最大最小值吗? (存在性)
- (唯一性: 全都是唯一的, 不考虑: 实际上大部分高中的问题都不用考虑唯一性)
- 最大/最小值是多少?
- 在自变量是几的时候取到?
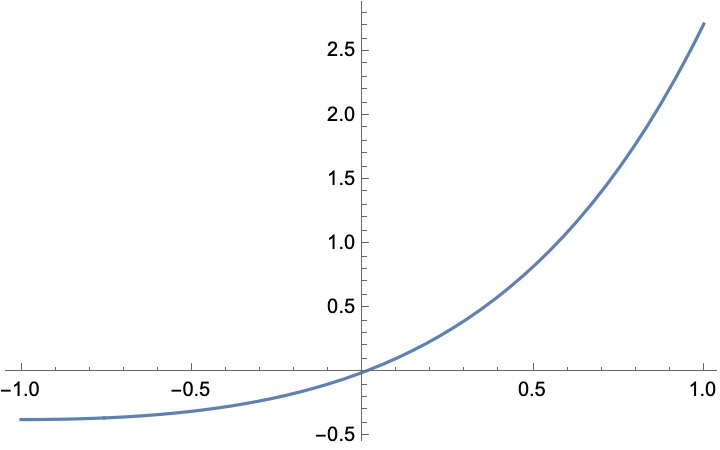
\[x \exp (x)
\]
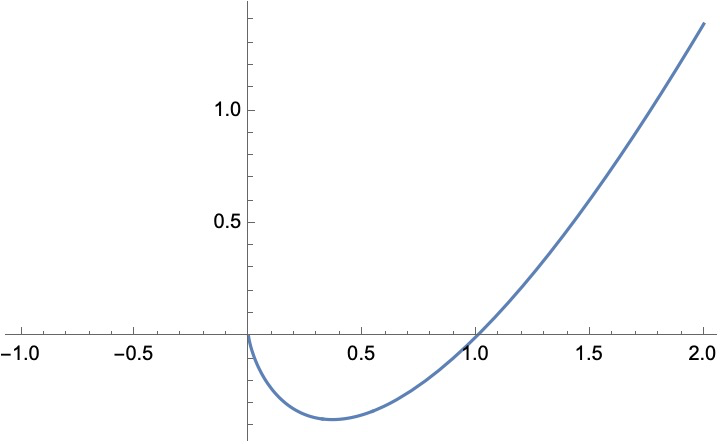
\[x \log (x)
\]
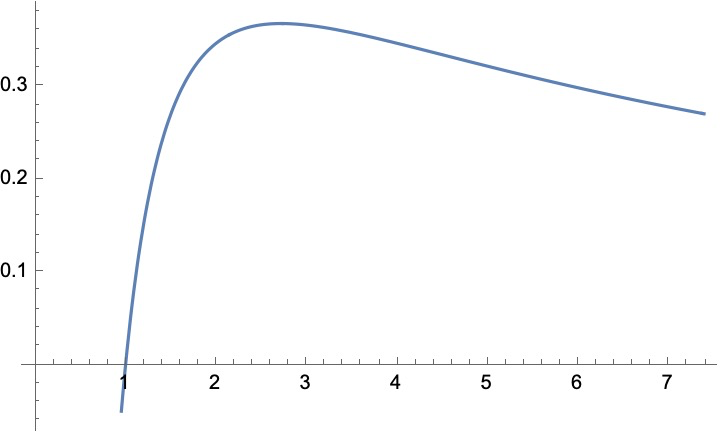
 $$
\frac{\log (x)}{x}
$$
$$
\frac{\log (x)}{x}
$$
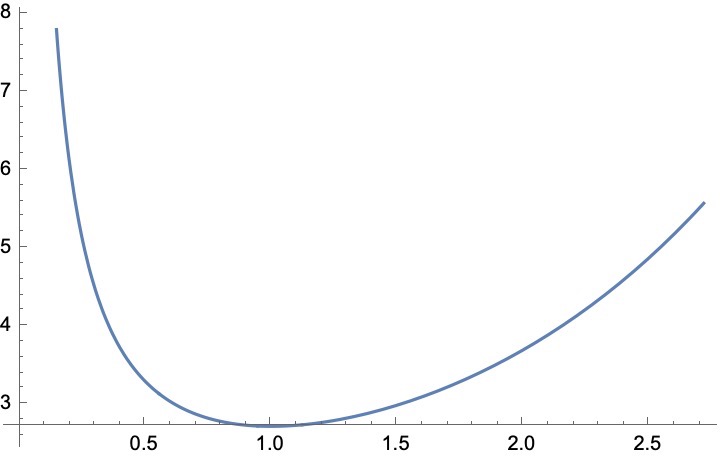
 $$
\frac{\exp (x)}{x}
$$
$$
\frac{\exp (x)}{x}
$$
补充:
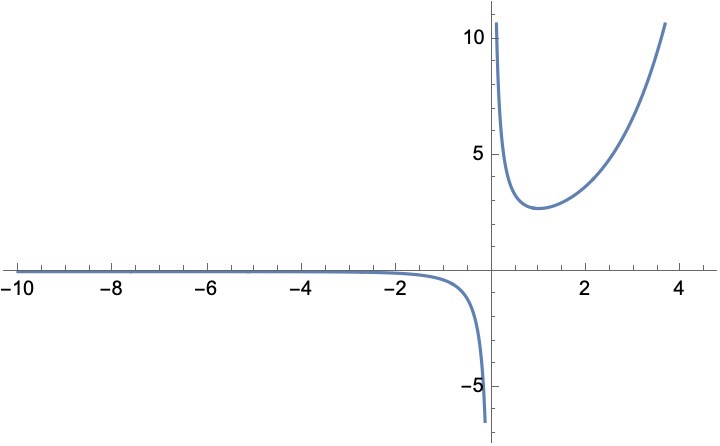
指数对数放缩
更进阶的感觉需要天赋, 或者说对函数的直觉? 提问:自身是否有这方面的天赋?是否需要拿这里的分数?
本质:泰勒/麦克劳林展开
等号成立的条件都显然, 所以省略.
\[e^x \geq x + 1 \quad
\]
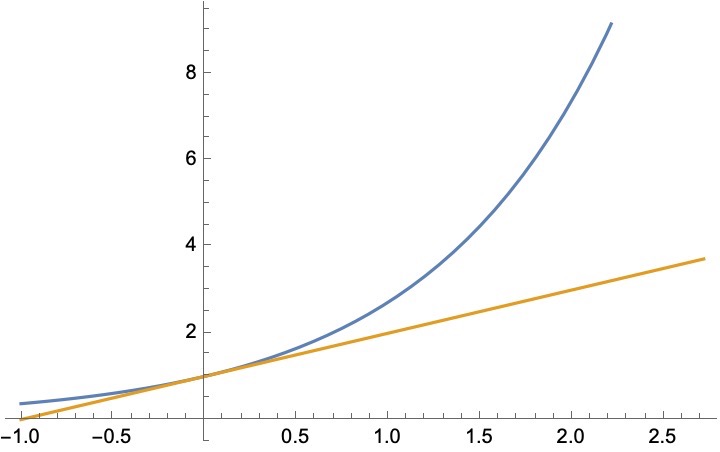 $$
\ln x \leq x - 1
$$
$$
\ln x \leq x - 1
$$
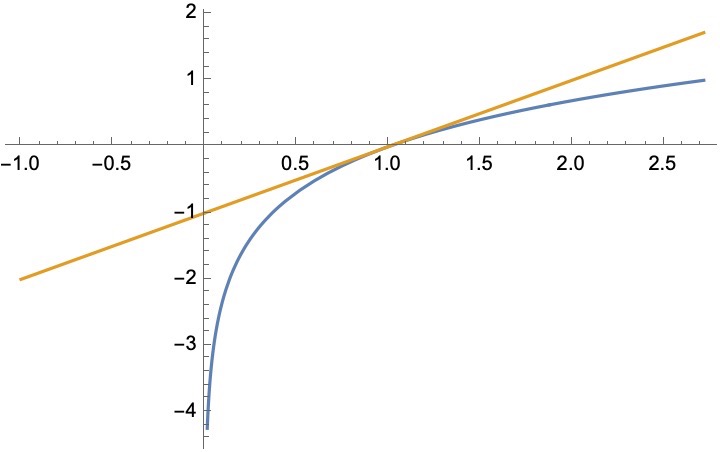
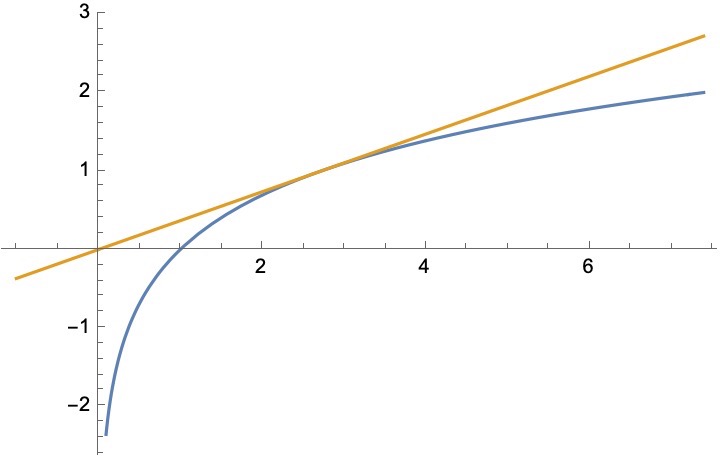
\[e^x \leq ex
\]
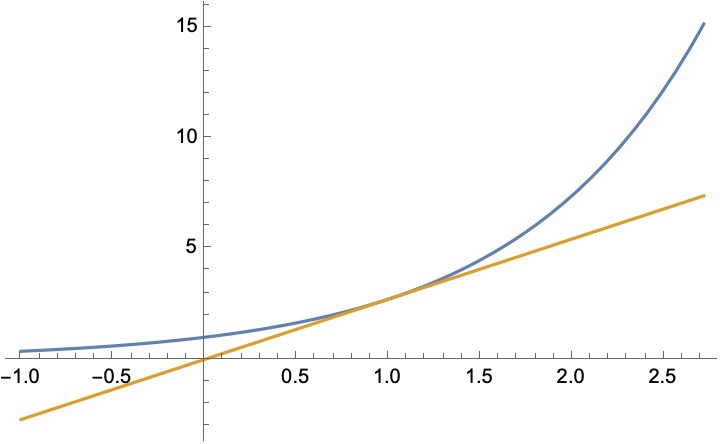 $$
\ln x \leq x/e
$$
$$
\ln x \leq x/e
$$
ALG 不等式
在算数平均和几何平均之间插入的一个元素:
\[\sqrt{a b}<\frac{a-b}{\ln a-\ln b}<\frac{a+b}{2} .
\]
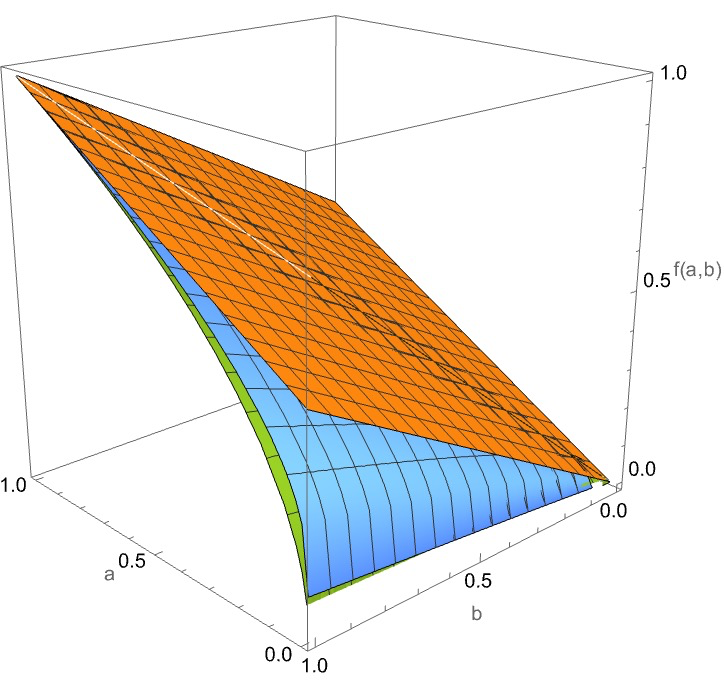
(中间蓝色的一层就是含有对数的成分)
🌰
Reference https://zhuanlan.zhihu.com/p/39442459
求证: 当 \(a>0\) 时, 不等式 \(e^{2 x}-a \ln x \geqslant 2 a+a \ln \frac{2}{a}\) 恒成立.
正常做法: 更换主元
放缩? 感觉更应该叫配凑, 但是用的是放缩的经验;
\[\left(e^{2 x}- 2ax \right) + \left( 2ax - a \ln x\right) \geqslant 2 a+a \ln \frac{2}{a}
\]
指数和对数在一起肯定是求导多少次都无法变没的,
回忆:
- 指数函数是一个向下凸的函数
- 对数函数是一个向上凸的函数
而且都只有一个凸起;
在放缩中指数和对数中间是夹着一个一次函数的;
所以能尝试构造最小值.
三角函数
\[\begin{aligned}
& \sin x=x-\frac{x^3}{3 !}+o\left(x^3\right) \\
& \cos x=1-\frac{x^2}{2}+o\left(x^2\right) \\
& \tan x=x+\frac{x^3}{3}+\frac{2}{15} x^5+o\left(x^5\right) \\
& \cot x=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}+o\left(x^3\right) \\
& \sec x=1+\frac{x^2}{2}+\frac{5}{24} x^4+o\left(x^4\right) \\
& \csc x=\frac{1}{x}+\frac{x}{6}+\frac{7}{360} x^3+o\left(x^3\right) \\
& \arcsin x=x+\frac{x^3}{6}++o\left(x^3\right) \\
& \arccos x=\frac{\pi}{2}-x-\frac{x^3}{6}+o\left(x^3\right) \\
& \arctan x=x-\frac{x^3}{3}+o\left(x^3\right) \\
& \operatorname{arccot} x=\frac{\pi}{2}-x+\frac{x^3}{3}+o\left(x^3\right)
\end{aligned}
\]
了解或者记住前三个即可.
练习
- 证明以下不等式, 并且如果可能, 你需要:
-
明确自变量范围;
-
确定取等条件;
\[\ln(t - 1) \geq \ln \ln t
\]
\[e^x > \ln x + 2
\]
\[\ln x + 1< e^{x/e}
\]
- 假设 \(x = (x_1, x_2, x_3)\) 是单位球上的一个点, 且 \(x_1,x_2, x_3 > 0\) 证明:
\[\ln x_1x_2x_3 \leq \sqrt{3} - 3.
\]
- 使用 \(e^x \geq ex\) 来证明 \(x - 1 \geq \ln x\). (另外两个关系也有类似的关系)
本文来自博客园,作者:miyasaka,转载请注明原文链接:https://www.cnblogs.com/kion/p/17495032.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号