Digital Watermark Implementation

Digital Watermarking Implementation Based on DWT, HD, and Singular Value Decomposition (MATLAB)

Introduction

Digital watermarking refers to embedding specific information into digital signals, which may include audio, images, or videos. When copying a signal with a digital watermark, the embedded information is also copied. Digital watermarks can be categorized into visible and invisible types. The former, known as visible watermarking, contains information that can be seen while viewing the image or video. Typically, visible watermarks include the name or logo of the copyright owner.

This digital watermarking implementation aims to embed a target image into a protected image while ensuring minimal impact on the visual quality of the original image. The watermark remains invisible without processing, and the method exhibits robustness—meaning the watermark can still be extracted even after the watermarked image undergoes damage, compression, distortion, rotation, or other attacks.

Principles

Embedding Process

• Host image → DWT2 → HD → SVD
• Logo → SVD
• \(\Sigma_{\text{output image}} = \Sigma_{\text{Origin}} + \alpha \Sigma_{\text{logo}}\)
• Inverse SVD (\(U \Sigma_{\text{output image}} V^*\)) → Inverse HD → Inverse DWT2

For simplicity, the algorithm extracts the "red" channel of the original RGB image, hereafter referred to as the "host image."

A 2D wavelet transform is applied to the host image, and the LL subband is selected for embedding—since the LL subband is less perceptible to the human eye.

The LL subband undergoes Hessenberg decomposition (HD), yielding matrix \(H\). Singular value decomposition (SVD) is then applied to \(H\) to obtain the singular value matrix \(\Sigma_{\text{Origin}}\).

The logo image (denoted as "logo") is also subjected to SVD, producing \(\Sigma_{\text{logo}}\).

The two singular value matrices are combined linearly to form the output matrix \(\Sigma_{\text{output image}}\):
\(\Sigma_{\text{output image}} = \Sigma_{\text{Origin}} + \alpha \Sigma_{\text{logo}}\)
where \(\alpha\) is a scaling factor controlling watermark strength.

The process is reversed by performing inverse SVD, inverse Hessenberg decomposition, and inverse 2D wavelet transform to reconstruct the watermarked image.

Extraction Process

DWT2 → HD → SVD → Computed extracted singular → Inverse SVD → Logo

The watermarked image undergoes the same transformations: 2D wavelet transform, Hessenberg decomposition, and SVD to obtain \(\Sigma_{\text{extract}}\). The original singular values are subtracted using the inverse linear combination, followed by inverse SVD to recover the logo.

Code Implementation

Embedding

origin_A = imread('origin.png');
origin_W = imread('logo.png');
[origin_A_n, origin_A_m] = size(origin_A);
A = imresize(origin_A, [origin_A_n, origin_A_n]);
W = imresize(origin_W, [origin_A_n, origin_A_n]);

alpha = 0.1;

RA = A(:,:,1);
RW = rgb2gray(W);
% figure,imshow(RA);
% figure,imshow(RW);

% dwt2
[LL,LH,HL,HH] = dwt2(RA,'db4');
% HD 
[P,H] = hess(LL);
% SVD on original Sigma
[HU,HS,HV] = svd(H);

% SVD on watermarked picture 
RW = imresize(RW,size(H));
[WU,WS,WV] = svd(double(RW));
% embed the watermark into the original graph
marked_HS = HS + alpha.* WS;
% inverse SVD
marked_H = HU * marked_HS * HV.';
% inverse HD
marked_LL = P * marked_H * P.';
% inverse DWT2
marked_img_Red = idwt2(marked_LL,LH,HL,HH,'db4');

marked_img_Red = imresize(marked_img_Red,size(RA));
marked_img = A;
marked_img(:,:,1) = uint8(marked_img_Red);
% figure,imshow(marked_img);
imwrite(marked_img,'marked_img.png');
key_img_svd = WU* HS *WV';
key_img(:,:,1) = WU;
key_img(:,:,2) = HS;
key_img(:,:,3) = WV;
imwrite(key_img,'key.png');
imwrite(key_img_svd,'keysvd.png');

Extraction

origin_A = imread('origin.png');
origin_W = imread('logo.png');
% test date collection
marked_A = imread('marked_img.png');
smear = imread('smear.png');
severe_smear = imread('severe_smear.png');
spin = imread('spin.png');
half = imread('half.png');
black_matrix = imread('black_matrix.png');
severe_compress = imread('severe_compress.png');

imwrite(ext(marked_A,origin_A,origin_W),'extract_marked_A.png');
imwrite(ext(smear,origin_A,origin_W),'extract_smear.png');
imwrite(ext(severe_smear,origin_A,origin_W),'extract_severe_smear.png');
imwrite(ext(spin,origin_A,origin_W),'extract_spin.png');
imwrite(ext(half,origin_A,origin_W),'extract_half.png');
imwrite(ext(black_matrix,origin_A,origin_W),'extract_black_matrix.png');
imwrite(ext(severe_compress,origin_A,origin_W),'extract_severe_compress.png');

function [mark] = ext(marked_A, origin_A, origin_W)
    [origin_A_n, origin_A_m] = size(origin_A);
    mA = imresize(marked_A,[origin_A_n,origin_A_n]);
    A = imresize(origin_A,[origin_A_n,origin_A_n]);
    W = imresize(origin_W,[origin_A_n,origin_A_n]);
    RmA = mA(:,:,1);
    RA = A(:,:,1);
    RW = rgb2gray(W);

    alpha =  0.1;

    % DWT
    [LL,LH,HL,HH] = dwt2(RmA,'db4');
    % HD 
    [P,H] = hess(LL);
    % SVD
    [HU, HS, HV] = svd(H);

    % dwt2
    [oLL,oLH,oHL,oHH] = dwt2(RA,'db4');
    % HD 
    [oP,oH] = hess(oLL);
    % SVD on original Sigma
    [oHU,oHS,oHV] = svd(oH);

    S = (HS - oHS)./alpha;

    % SVD on watermark
    RW = imresize(RW,size(S));
    [WU,WS,WV] = svd(double(RW));
    mark = WU * S * WV.';
%     comp = WU * WS * WV.';
%     figure,imshow(uint8(mark));
%     figure,imshow(uint8(comp));
    mark = uint8(mark);
end

Examples

Original Image, Logo, and Watermarked Image

Original Image

Logo

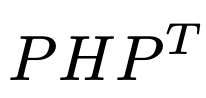
Watermarked Image

Smearing Attack

Attack Example

Extracted Watermark

Severe Smearing Attack

Attack Example

Extracted Watermark

The outline remains discernible, but the quality is degraded.

Rotation Attack

Attack Example

Extracted Watermark

Unaffected, as SVD discards rotational information.

Block Damage Attack (Small Squares)

Attack Example

Extracted Watermark

Photoshop Auto-Color Attack

Attack Example

Extracted Watermark

Only the outline is visible; quality is poor.

Cropping Attack

Attack Example

Extracted Watermark

Compression Attack

Attack Example

Extracted Watermark

Highly effective.

Analysis and Conclusion

The algorithm demonstrates strong robustness against cropping, compression, and minor image damage, producing extractable watermarks with good clarity. However, its performance is suboptimal in other scenarios due to:

1. Inherent weaknesses against certain attacks.
2. Fixed \(\alpha\) value instead of an optimized adaptive selection.
3. Simplifications in the implementation compared to the original paper.

References

Liu, Junxiu, Jiadong Huang, Yuling Luo, Lvchen Cao, Su Yang, Duqu Wei, and Ronglong Zhou. 2019. "An Optimized Image Watermarking Method Based on HD and SVD in DWT Domain." IEEE Access PP (99): 1–1. doi:10.1109/ACCESS.2019.2915596.