专题讨论2
数据结构专题讨论2:树与查找
----表达式树(网安2411班于鸿硕、吴承桓小组)
一、题目分析与思路设计
求解本题,小组分别从用表达式树和用栈二种解决方法进行分析。通过对计算表达式进行分析,我们发现在解决表达式储存和计算问题中,两种解决方法都需要先用栈把中缀表达式转化为后缀表达式,而后分别存入不同数据结构体进行计算,遂有如下设计:
//伪代码:
// 表达式树法:
// 定义表达式树节点结构
结构体 TreeNode {
字符串 val // 节点值,可以是数字或运算符
TreeNode* left // 左子树指针
TreeNode* right // 右子树指针
}
// 判断字符是否为数字
函数 isDigit(字符 ch) 返回 布尔值:
返回 ch >= '0' 且 ch <= '9'
// 获取运算符优先级
函数 getPriority(字符 op) 返回 整型:
如果 op 是 '+' 或 '-' 则 返回 1
如果 op 是 '*' 或 '/' 则 返回 2
返回 0 // 其他字符(如括号)
// 中缀表达式转后缀表达式
函数 infixToPostfix(字符串 infix) 返回 字符串:
初始化 opStack 为字符栈
初始化 postfix 为空字符串
对于 infix 中的每个字符 ch:
如果 ch 是空格 则 跳过
如果 isDigit(ch) 为真:
postfix 追加 ch
否则 如果 ch 是 '(':
opStack.push(ch)
否则 如果 ch 是 ')':
当 opStack 非空 且 栈顶不是 '(':
postfix 追加 opStack.top()
opStack.pop()
opStack.pop() // 弹出 '('
否则: // 处理运算符
当 opStack 非空 且 getPriority(opStack.top()) >= getPriority(ch):
postfix 追加 opStack.top()
opStack.pop()
opStack.push(ch)
// 弹出栈中剩余运算符
当 opStack 非空:
postfix 追加 opStack.top()
opStack.pop()
返回 postfix
// 根据后缀表达式构建表达式树
函数 buildTree(字符串 postfix) 返回 TreeNode*:
初始化 nodeStack 为 TreeNode* 栈
对于 postfix 中的每个字符 ch:
如果 isDigit(ch) 为真:
创建新节点 newNode(ch)
nodeStack.push(newNode)
否则: // 处理运算符
创建新节点 newNode(ch)
newNode->right = nodeStack.top()
nodeStack.pop()
newNode->left = nodeStack.top()
nodeStack.pop()
nodeStack.push(newNode)
如果 nodeStack 非空 则 返回 nodeStack.top()
否则 返回 NULL
// 递归计算表达式树的值
函数 calculate(TreeNode* root) 返回 整型:
如果 root 为 NULL 则 返回 0
如果 root 是叶节点 (左右子节点均为NULL):
将 root->val 转换为整数 num
返回 num
left = calculate(root->left)
right = calculate(root->right)
根据 root->val 的值:
如果是 "+": 返回 left + right
如果是 "-": 返回 left - right
如果是 "*": 返回 left * right
如果是 "/": 返回 left / right
返回 0 // 默认值
// 主程序
函数 main() 返回
// 直接用栈法:
输入:后缀表达式 postfix
输出:表达式计算结果
初始化:空栈 operand_stack
对 postfix 中的每个字符 token:
if token 是数字:
将 token 转换为数值 num
将 num 压入 operand_stack 栈
else if token 是运算符(+、-、*、/):
弹出 operand_stack 栈顶元素作为右操作数 right
弹出 operand_stack 栈顶元素作为左操作数 left
switch token:
case '+':
result = left + right
case '-':
result = left - right
case '*':
result = left * right
case '/':
if right == 0:
抛出除零错误
result = left / right
将 result 压入 operand_stack 栈
返回 operand_stack 的栈顶元素(即最终计算结果)
二、主要运行过程流程图
graph TD;
A[输入表达式]-->B[中缀表达式通过栈转化为后缀形式];
B-->|遍历后缀表达式|c["逢操作数入栈、逢运算符出栈两个操作数作为孩子结点"];
c-->g[将操作符节点入栈];
g-->z["表达式树构建完成,返回根节点"]
z-->e["递归计算"];
e-->f[计算结果];
B-->|直接用栈|e;
三、代码及运行结果
1.表达树法:
#include <iostream>
#include <stack>
#include <string>
using namespace std;
// 表达式树节点结构
struct TreeNode {
string val; // 节点值,可以是数字或运算符
TreeNode* left; // 左子树指针
TreeNode* right; // 右子树指针
// 构造函数
TreeNode(string x) {
val = x;
left = NULL;
right = NULL;
}
};
// 判断字符是否为数字
bool isDigit(char ch) {
return ch >= '0' && ch <= '9';
}
// 获取运算符优先级
// 返回值越大表示优先级越高
int getPriority(char op) {
if (op == '+' || op == '-') return 1; // 加减法优先级较低
if (op == '*' || op == '/') return 2; // 乘除法优先级较高
return 0; // 其他字符(如括号)优先级最低
}
// 中缀表达式转后缀表达式(逆波兰表示法)
// 参数:infix - 中缀表达式字符串
// 返回:对应的后缀表达式字符串
string infixToPostfix(const string& infix) {
stack<char> opStack; // 运算符栈
string postfix; // 存储后缀表达式结果
// 遍历中缀表达式每个字符
for (int i = 0; i < infix.size(); i++) {
char ch = infix[i];
if (ch == ' ') continue; // 跳过空格
// 处理数字
if (isDigit(ch)) {
postfix += ch; // 数字直接加入后缀表达式
}
// 处理左括号
else if (ch == '(') {
opStack.push(ch); // 左括号直接入栈
}
// 处理右括号
else if (ch == ')') {
// 弹出栈顶元素直到遇到左括号
while (!opStack.empty() && opStack.top() != '(') {
postfix += opStack.top();
opStack.pop();
}
opStack.pop(); // 弹出左括号但不加入后缀表达式
}
// 处理运算符
else {
// 弹出栈顶优先级不低于当前运算符的所有运算符
while (!opStack.empty() && getPriority(opStack.top()) >= getPriority(ch)) {
postfix += opStack.top();
opStack.pop();
}
opStack.push(ch); // 当前运算符入栈
}
}
// 弹出栈中剩余的所有运算符
while (!opStack.empty()) {
postfix += opStack.top();
opStack.pop();
}
return postfix;
}
// 根据后缀表达式构建表达式树
// 参数:postfix - 后缀表达式字符串
// 返回:表达式树的根节点指针
TreeNode* buildTree(const string& postfix) {
stack<TreeNode*> nodeStack; // 节点栈,用于构建表达式树
// 遍历后缀表达式每个字符
for (int i = 0; i < postfix.size(); i++) {
char ch = postfix[i];
// 处理数字
if (isDigit(ch)) {
// 创建数字节点并入栈
nodeStack.push(new TreeNode(string(1, ch)));
}
// 处理运算符
else {
// 创建运算符节点
TreeNode* node = new TreeNode(string(1, ch));
// 运算符的右操作数是栈顶元素
node->right = nodeStack.top();
nodeStack.pop();
// 运算符的左操作数是新的栈顶元素
node->left = nodeStack.top();
nodeStack.pop();
// 将运算符节点入栈
nodeStack.push(node);
}
}
// 栈顶元素即为表达式树的根节点
return nodeStack.empty() ? NULL : nodeStack.top();
}
// 递归计算表达式树的值
// 参数:root - 表达式树的根节点指针
// 返回:表达式的计算结果
int calculate(TreeNode* root) {
if (root == NULL) return 0; // 空树返回0
// 如果是叶节点(数字节点)
if (root->left == NULL && root->right == NULL) {
int num = 0;
// 将字符串转换为整数
for (int i = 0; i < root->val.size(); i++) {
num = num * 10 + (root->val[i] - '0');
}
return num;
}
// 递归计算左子树的值
int left = calculate(root->left);
// 递归计算右子树的值
int right = calculate(root->right);
// 根据运算符计算左右子树的结果
if (root->val == "+") return left + right;
if (root->val == "-") return left - right;
if (root->val == "*") return left * right;
if (root->val == "/") return left / right;
return 0; // 默认返回0
}
int main() {
string expr = "(3+5)*(10-4)"; // 测试表达式
string postfix = infixToPostfix(expr); // 转换为后缀表达式
TreeNode* root = buildTree(postfix); // 构建表达式树
int result = calculate(root); // 计算结果
// 输出信息
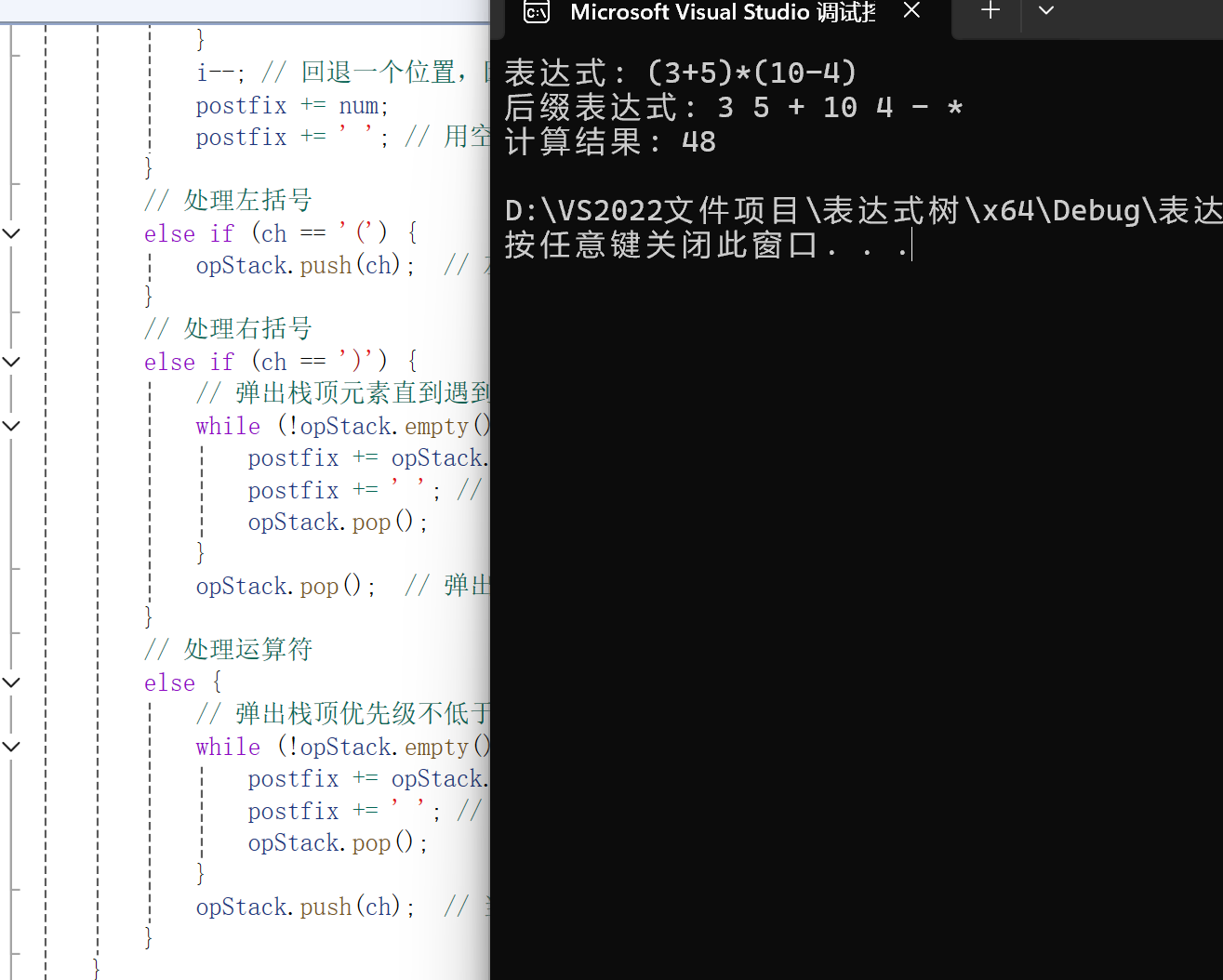
cout << "表达式: " << expr << endl;
cout << "后缀表达式: " << postfix << endl;
cout << "计算结果: " << result << endl;
return 0;
}
运行截图:
2.直接用栈法:
// 栈方法计算后缀表达式的值
double evaluatePostfix(const vector<char>& postfix) {
stack<double> operands;
for (char c : postfix) {
if (isdigit(c)) {
operands.push(c - '0');
} else if (isOperator(c)) {
double right = operands.top();
operands.pop();
double left = operands.top();
operands.pop();
switch (c) {
case '+':
operands.push(left + right);
break;
case '-':
operands.push(left - right);
break;
case '*':
operands.push(left * right);
break;
case '/':
if (right == 0) {
cerr << "Error: Division by zero!" << endl;
return 0;
}
operands.push(left / right);
break;
}
}
}
return operands.top();
}
int main() {
double stackResult = evaluatePostfix(postfix);
cout << "Stack method result: " << stackResult << endl;
}
四、分析与结论
在实验过程中,我们发现:
传统的计算表达式的方法(即直接用栈法)
可以通过一个栈实现该计算功能,代码相对简洁简单,占用内存空间略为轻量,不需要递归遍历使得计算效率更高。但是结构不够直观,用户无法对表达式进行分析和修改,同时只适用于加减乘除基本操作。
复杂度分析:
- 时间复杂度:
- 中缀转后缀:遍历表达式一次,时间复杂度为 (O(n))。
- 计算后缀表达式:遍历后缀表达式一次,时间复杂度为 (O(n))。
- 综上,总时间复杂度为 (O(n) + O(n) = O(n))。
- 空间复杂度:
- 中缀转后缀:栈中最多存储 (O(n)) 个运算符(如大量左括号场景)。
- 计算后缀表达式:栈中最多存储 (O(n/2)) 个操作数(如交替出现操作数和运算符),仍为 (O(n))。
- 综上,空间复杂度为 (O(n))。
表达式树方法
表达式树能直观地向用户表示表达式的结构,便于理解和分析,甚至拓展至修改、化简和求导等高级操作(可直接操作树节点),也能够处理含括号和复杂运算符优先级的表达式。但是实现偏复杂,需要大量代码和额外内存空间支持两个数据结构。
复杂度分析:
- 时间复杂度:
- 中缀转后缀:遍历表达式一次,时间复杂度为 (O(n))。
- 构建表达式树:遍历后缀表达式一次,每个元素处理一次,时间复杂度为 (O(n))。
- 计算表达式树值:后序遍历每个节点一次,时间复杂度为 (O(n))。
- 综上,总时间复杂度为 (O(n) + O(n) + O(n) = O(n))。
- 空间复杂度:
- 中缀转后缀:栈中最多存储 (O(n)) 个运算符(如大量左括号场景)。
- 构建表达式树:存储 n 个节点(每个表达式元素对应一个节点),空间复杂度为 (O(n))。
- 计算表达式树值:递归调用栈深度最大为树高(最坏 (O(n)),如退化为链表的树)。
- 综上,空间复杂度主要由存储树节点决定,为 (O(n))。
最后,我们对比列出如下表格:
| 方面 | 表达式树 | 直接用栈 |
|---|---|---|
| 时间复杂度 | 构建(O (n)) + 计算(O (n)) | 转后缀(O (n)) + 计算(O (n)) |
| 空间复杂度 | O (n)(存储整棵树) | O (n)(栈空间,无需存储树) |
| 内存占用 | 略微大(两个数据结构) | 略微小(一个栈) |
| 适用户性 | 结构清晰 | 用户不可见其结构 |
| 可拓展性 | 可进行修改、化简及其他高级操作 | 无 |
综上所分析,表达式树具有操作拓展性高的显著优势,可以在计算中实时根据需要进行修改和调整,可应用于更多种实际场景
五、讨论
经资料查阅整合,表达式树除了计算表达式求值还有下列功能:
- 代码生成:在编译器和代码生成器中,表达式树可以作为中间表示形式。将高级语言中的表达式转换为表达式树后,再根据目标平台的指令集和规范,将表达式树生成对应的机器码或其他目标代码。这样可以方便地对表达式进行优化和生成高效的代码。
- 语法分析与验证:在编译过程中,词法分析器和语法分析器将输入的源代码转换为表达式树,以此来检查表达式的语法结构是否正确。例如,在检查一个复杂的数学表达式或逻辑表达式是否符合语法规则时,表达式树能够清晰地展示表达式的结构,帮助发现语法错误。
- 数据查询与筛选:在数据库查询语句的处理中,表达式树可以用来表示查询条件。例如,对于查询语句
SELECT * FROM students WHERE age > 18 AND grade = 'A',可以将其转换为表达式树来进行解析和处理,以便数据库系统能够根据表达式树来执行相应的查询操作,高效地筛选出符合条件的数据。 - 函数式编程与 Lambda 表达式处理:在函数式编程语言中,表达式树常用于表示 Lambda 表达式或其他函数式构造。它使得对函数的操作和转换更加方便,例如可以对函数进行组合、柯里化等操作,还可以在运行时动态地生成和修改函数。
- 优化与变换:基于表达式树的结构,可以对表达式进行各种优化操作。例如,常量折叠、公共子表达式消除、代数化简等。通过分析表达式树的节点和结构,识别出可以优化的部分,并进行相应的变换,以提高表达式的计算效率或代码的执行效率。
- 可视化与调试:表达式树可以被可视化,以帮助开发人员理解复杂表达式的结构和执行流程。在调试过程中,通过查看表达式树的状态和节点值,可以更容易地发现表达式求值过程中出现的问题,有助于快速定位和解决错误。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号