算法设计与分析4_Divide & Conquer

与课本对应关系
教材Chapter 4 & Chapter 7
Chapter 4. 分治策略
Chapter 7. Quick Sort
考试考三种递归法

算法设计与分析4_递归式和分治法

Main Topics (Cont.):

掌握设计有效的分治策略算法及时间性能分析(本章重点讨论)
而时间性能分析其实就是有效分治策略算法设计的依据
通过下面的范例学习分治策略设计技巧
①二分搜索技术(Binary Search)；
②归并排序和快速排序(Merge Sort & Quick Sort)；
③大整数乘法；
④Strassen矩阵乘法；
⑤最接近点对问题Closest pairwise points；
⑥Convex Hull Finding Problem；

递归式和分治法

直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数；
由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小至很容易直接求出其解的程度时终止。这自然导致递归过程的产生；

分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

Now, we will give some recursion instances in the following part.
factorial function

例1factorial function阶乘函数

边界条件与递归方程是递归函数的两个要素，递归函数只有具备了这两个要素，才能在有限次计算后得出结果。

例2Fibonacci数列

第n个Fibonacci数可递归地计算如下：

int Fibonacci (int n){
  if (n <= 1) return 1;
  return Fibonacci(n-1) + Fibonacci(n-2);
}

证Fibonacci数列的递归算法复杂度是$2^n$：深度为n的二叉递归树
最快算法是logn的时间

除了直接递归以外的另4种求解方案：
方法1：用户自定义一个栈，模拟系统递归调用工作栈
方法2：递推关系式的优化时间O(n), 空间O(n)
方法3：求解通项公式时间O(1)
方法4：分治策略时间O(log2n)

Non-recursive Fibonacci Iterative Function

int Fibonacci (int n)
/* fibonacci: iterative version*/
{
  int last_but_one; // second previous Fibonacci number, Fi−2
  int last_value; // previous Fibonacci number, Fi−1
  int current; // current Fibonacci number Fi
  if (n <= 0) return 0;
    else if (n == 1) return 1;
    else {
        last_ but_ one = 0;
        last_ value = 1;
        for (int i = 2; i <= n; i++) {
          current = last_but_one + last_value;
          last_but_ one = last_value;
          last_value = current;
        }
  return current;
  }
}

例4 排序问题

写出归并排序的非递归算法

有些问题表面上不是递归定义的,但可通过分析,抽象出递归的定义

就地算法设计全排列

写一个就地生成n个元素a1, a2, …, an全排列(n!) 的算法，要求算
法终止时保持a1, a2, …, an原状。

设R={r}是要进行排列的四个元素,R_i=R-(r_i)。

集合X中元素的全排列记为perm(X).

perm(r) 表示在全排列perm(X)的每一个排到后加上后缀得到

内定义如下:

算法:以A[0..7]为例

void permute (char A[], int n) { //外部调用时令 n=7 
 if (n==0)
    print (A); // 打印A[0...7]
  else {
    permute(A,n-1); //求A[0..n-1]的全部排列。1**子问题不用交换
    for (i=n-1; i>=0; i--) {
       Swap(A[i], A[n]); // 交换a和a内容,说明为引用
       permute(A,n-1); // 求A[0..n-1] 全排列
       Swap(A[i], A[n]); //交换,恢复原状
   }//endfor
  }//endif
}

时间:$O(2^n) <n! <O(n^n)$ 所以实验时,n不能太大

整数划分

将正整数n表示成一系列正整数之和：n=n1+n2+…+nk，其中n1≥n2≥…≥nk≥1，k≥1。
正整数n的这种表示称为正整数n的划分。求正整数n的不同划分个数。

本题较难。在本例中，如果设p(n)为正整数n的划分数，则难以找到递归关系，因此考虑增加一个自变量：将最大加数n1不大于m的划分个数记作q(n,m)。可以建立q(n,m)的如下递归关系。

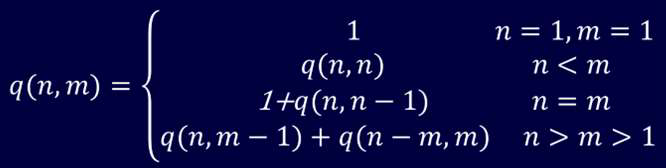
int q (int n, int m){
  if((n<1)||(m<1)) return 0;
  if((n==1)||(m==1)) return 1;
  if(n<m) return q(n,n);
  if(n==m) return q(n,m-1)+1;
  return q(n,m-1)+q(n-m,m);
}

n阶Hanoi塔问题

尾递归

当函数的最后一个操作是递归时，称为尾递归。

反例：对于求阶乘函数最后一步是n*f(n-1)，并不是尾递归，因为最后一步是乘法。

因为stack frame的存在，尾递归的效率比一般的效率高（编译器检测到尾递归是自动进行优化：覆盖当前活动记录，不是新建活动记录（overwrite））

如何将求阶乘改为尾递归
引入新参数，表示递归的深度

def factorial_tail_recursive(n, acc=1):
    if n == 1:
        return acc
    else:
        return factorial_tail_recursive(n - 1, n * acc)

说明：

acc 参数：acc 是一个累积器，保存着当前计算到的中间结果。初始值为 1，即阶乘计算的起点。
尾递归调用：在 factorial_tail_recursive 中，递归调用是函数的最后一步。它直接调用 factorial_tail_recursive(n - 1, n * acc)，并没有其他操作跟在调用后面。
累积计算：每次递归时，当前的 n 乘以累积的结果 acc，并传递给下一个递归调用。
如何消除汉诺塔的尾递归?
原问题：

def hanoi(n, source, target, auxiliary):
    if n == 1:
        print(f"Move disk 1 from {source} to {target}")
    else:
        hanoi(n-1, source, auxiliary, target)
        print(f"Move disk {n} from {source} to {target}")
        hanoi(n-1, auxiliary, target, source)

递归算法优缺点

优点：结构清晰，可读性强，而且容易用数学归纳法来证明算法的正确性，因此它为设计算法、调试程序带来很大方便。
缺点：递归算法的运行效率较低，无论是耗费的计算时间还是占用的存储空间都比非递归算法要多。

解决方法：在递归算法中消除递归调用，使其转化为非递归算法

采用一个用户定义的栈来模拟系统的递归调用工作栈。
该方法通用性强，但本质上还是递归，只不过人工做了本来由编译器做的事情，优化效果不明显。
用递推来实现递归函数。
通过变换能将一些递归转化为尾递归，从而迭代求出结果。

后两种方法在时空复杂度上均有较大改善，但其适用范围有限。

递归至非递归机械转化

机械地将任何一个递归程序转换为与其等价的非递归程序
 五条规则：
(1) 设置一个栈（不妨用Ｓ表示），并且开始时将其置为空。
(2) 在子程序入口处设置一个标号（不妨设为L0）。
(3) 对子程序中的每一递归调用，用以下几个等价操作来替换：
a) 保留现场：开辟栈顶存储空间，用于保存返回地址（不妨用
b) Li，i=1,2,3，…）、调用层中的形参和局部变量的值（最外层调
用不必考虑）。
c) 准备数据：为被调子程序准备数据，即计算实在参数的值,并赋给
对应的形参
d) 转入（子程序）执行, 即执行goto L0。
e) 在返回处设一个标号Li(i=1,2,3，…)，并根据需要设置以下语句：
若函数需要返回值，从回传变量中取出所保存的值并传送到相应
的位置。
(4) 对返回语句，可用以下几个等价操作来替换：
如果栈不空，则依次执行如下操作，否则结束本子程序，返回。
a) 回传数据：若函数需要返回值，将其值保存到回传变量中。
b) 恢复现场：从栈顶取出返回地址（不妨保存到Ｘ中）及各变量
、形参值，并退栈。
c) 返回：按返回地址返回（即执行goto Ｘ）。
(5) 对其中的非递归调用和返回操作可照搬。

🌟分治法

作用:分析递归算法的运行时间

三种方法(P37)

替换法、迭代法(递归树法)、通用法(master method)

分治算法设计

将一个问题分解为与原问题相似但规模更小的若干子问题, 递归地解这些子问题,然后将这些子问题的解结合起来构成原问题的解。
这种方法在每层递归上均包括三个步骤：

Divide(分解):将问题划分为若干个子问题
Conquer(求解):递归地解这些子问题;若子问题Size足够小,则直接解决之
Combine(组合):将子问题的解结合成原问题的解

其中的第二步：递归调用或直接求解(递归终结条件)
有的算法“分解”容易，有的则“组合”容易

容易=耗时少，有的算法分解容易，有的算法组合容易

举例
归并排序 https://www.cnblogs.com/kingwz/p/15674088.html

分解：把n个待排序元素划分为两个Size为n/2的子序列
求解：递归调用归并排序将这两个子序列排序，若子序列长度为1时，已自然有序，无需做任何事情(直接求解)
组合：将这两个已排序的子序列合并为一个有序的序列

显然，分解容易(一分为二)，组合难。

快速排序： https://www.cnblogs.com/kingwz/p/15747401.html#快速排序

分解难，组合易。A[1…k-1] ≤ A[k] ≤ A[k+1…n]

人们从大量实践中发现，在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。

分治算法时间性能分析

设T(n)是Size为n的执行时间，

若Size足够小，如n≤C (常数)，则直接求解的时间为θ(1)，否则：

设完成划分的时间为D(n)
设分解时,划分为a个子问题,每个子问题为原问题的1/b, 则解各子问题的时间为aT(n/b)
设组合时间C(n)

计算时可以忽略细节：

设T(n)是Size为n的执行时间,若Size足够小,如n≤C(常数),则直接求解的时间为(1)

一般地，解递归式(Recurrence,定义见P37)时可忽略细节

假定函数参数为整数，如2T(n / 2)应为$T(\lceil n / 2 \rceil)$或$T(\lfloor n / 2 \rfloor )$
边界条件可忽略，当n较小时$T(n)=\theta (1)$
因为这些细节一般只影响常数因子的大小，不改变量级。

∴求解时，先忽略细节，然后再决定其是否重要(P38)
但下面讨论时，我们尽量注意细节！

例如：二路归并递归函数的时间：$Tn=O1+2T（\frac{n}{2}）+On$

替换法(代入法, Page 47~49)

代入法就是用猜测的解代入到递归式中。

步骤：

按照经验猜测解;
用数学归纳法确定常数C，证明解正确(注意证明边界情况也成立)

例1: 求解 $T(n)=2T(\frac{n}{2})+n$的上界
【1 证明上界】
猜测$T(n)=2T(\frac{n}{2})+n$的上界为$T(n) = O(nlgn)$
即要证T(n)≤cnlgn,对某个常数c>0成立

假定对于所有正数m,满足m<n均成立

假定它对于$\lfloor n/2 \rfloor$成立$,i.e.. T([n/2)≤c_n/2]1g_n/2]$, 将它代入递归式中

$T(n)≤2(c_n/2|lg|n/2])+n$

$≤cnlg(n/2)+n$

$=cnlgn-cnlg2+n=cnlgn-cn+n≤cnlgn$ 只要c≥1

【2 证明边界条件亦成立】

假定 $T(0) = 0$, $T(1) = 1$
而 $T(1) <= C * 1lg * 1 = 0$ 不成立
但渐近界只要证 $T(n) <= cnlgn for n≥n_0$即可
.. $T(2) = 2T(1) + 2 = 4$
$T(2) <= C * 2lg * 2 = 2C$ 只要 $c >= 2$ 即可

细节修正

例2

该幻灯片介绍了替换法中的细节修正，重点解释了如何通过减去一个低阶项，使数学归纳法能够更容易地证明猜测解的正确性。

主要内容包括：

问题背景：
- 猜测解有时是正确的，但数学归纳法可能不能直接证明细节部分。这是因为数学归纳法的假设强度不足以证明细节。
- 通过减去猜测解中的一个低阶项，可以使归纳假设满足证明要求。
例子：
递归式：
$ T(n) = T(\lfloor n/2 \rfloor) + T(\lceil n/2 \rceil) + 1 $
- 显然，该递归式的解为 $ O(n) $，即要证明 $ T(n) \leq cn $。
证明过程（pf）：
- 初步猜测解：$ T(n) \leq c(\lfloor n/2 \rfloor) + c(\lceil n/2 \rceil) + 1 $。
- 由归纳假设代入，得到：$ T(n) \leq cn + 1 $。
- 该表达式不含 $ T(n) \leq cn $，因此不满足证明要求。
细节修正：
- 修正猜测解，减去一个常数项：$ T(n) \leq cn - b $（常数 $ b \geq 0 $）。
- 继续推导得到：
  $ T(n) \leq c(\lfloor n/2 \rfloor) - b + c(\lceil n/2 \rceil) - b + 1 $
  $ = cn - 2b + 1 \leq cn - b $，只要 $ b \geq 1, c > 0 $。

避免陷阱

该幻灯片的内容是关于替换法的一个小节，重点讲解了如何避免陷入证明递归关系时的错误。

关键点：

避免陷阱：
- 在证明递归关系时，类似于使用数学归纳法，容易因为渐近记号的使用不当产生错误。
例子：
给定递归关系：
$T(n) = 2T(\lfloor n/2 \rfloor) + n$
- 错误的猜测：
  $T(n) \leq cn$
  实际上正确答案应该是 $n \log n$。
证明过程（pf）：
代入假设，得到：
$T(n) \leq 2(c \lfloor n/2 \rfloor) + n \leq cn + n$

这个不等式的结果是错误的，无法证明 $T(n) \leq cn$，因此说明了在这种情况下，需要更精确的形式，而不是简单地假设线性关系。

总结：
在使用替换法证明递归式时，应该小心处理渐近记号，并且需要进行更细致的推导，避免类似“$T(n) \leq cn$”这种不准确的猜测。

变量变换

证明过程

课本P52

迭代法

关键点：展开：

在求解递归式时，需要无须猜测，展开递归式。将递归式展开为仅依赖于 $n$ 和边界条件的和式，然后使用求和方法来确定边界。

通过迭代法展开，可以逐步展开递归层次，最终将递归关系转化为非递归的形式，方便求解复杂度。

Keys

达到边界条件所需的迭代次数
迭代过程中的和式。若在迭代过程中已估计出解的形式, 亦可用替换法
当递归式中包含floor和ceiling函数时,常假定参数为一个整数次幂,以简化问题。例如下例可假定n=4k(k≥0的整数),但这样T(n)的界只对4的整数幂成立。下节方法可克服此缺陷。

例 $3T(\lfloor n/4 \rfloor) + n$

例求解 $T(n) = 3T(\lfloor n/4 \rfloor) + n$

$T(n) = 3T(\lfloor n/4 \rfloor) + n$

$T(n) = 3[3T(\lfloor n/4^2 \rfloor) + \lfloor n/4 \rfloor] + n = 3^2T(\lfloor n/4^2 \rfloor) + 3\lfloor n/4 \rfloor + n$（因为$T(\lfloor n/4 \rfloor) = 3T(\lfloor n/4^2 \rfloor) + \lfloor n/4 \rfloor$）

$T(n) = 3^3T(\lfloor n/4^3 \rfloor) + 3^2\lfloor n/4^2 \rfloor + 3\lfloor n/4 \rfloor + n$ （因为$T(\lfloor n/4^2 \rfloor) = 3T(\lfloor n/4^3 \rfloor) + \lfloor n/4^2 \rfloor$，）

通过不断展开，规律逐渐显现出来。第 $k$ 层的展开形式为：

$ T(n) = 3^k T(\lfloor n/4^k \rfloor) + \sum_{i=0}^{k-1} 3^i \cdot \left\lfloor \frac{n}{4^i} \right\rfloor $

【步骤 2: 终止条件】
不妨设最后项为 i项： $3^i T(\lfloor n/4^i \rfloor)$ 边界应为$\left\lfloor \frac{n}{4^i} \right\rfloor <=1$ 即$i>=log_4n$
所以当 $i=log_4n$ 时，有 $T(1) = \theta (1)$

递归终止于 $n$ 变得足够小的时候，例如 $T(1)$，通常是常数（假设 $T(1) = O(1)$）。当 $n/4^k$ 接近 1 时，递归结束。也就是说，递归的层数 $k$ 满足 $n/4^k \approx 1$，即 $k \approx \log_4 n$。

【步骤 3: 计算复杂度】
代入递归终止条件 $T(1) = O(1)$ 后，我们得到：

$T(n) = 3^{\log_4 n} \cdot O(1) + \sum_{i=0}^{\log_4 n - 1} 3^i \cdot \frac{n}{4^i}$
$<= n \sum_{i=0}^{ \infty} （\frac{3}{4})^i + \theta (n^{log_4 3})$ Note：$n^{log_4 3} = 3^{log_4 n}$
$=4n+o(n)$ //小o
$=O(n)$ //大O

点击查看代码

**首先确定树的深度为$log_{4}n$**

步骤 1: 展开递归式
我们首先展开几层递归：

- 第 1 层：  
  $T(n) = 3T(\lfloor n/4 \rfloor) + n$

- 第 2 层：  
  $T(\lfloor n/4 \rfloor) = 3T(\lfloor n/4^2 \rfloor) + \lfloor n/4 \rfloor$，  
  代入得到：  
  $T(n) = 3[3T(\lfloor n/4^2 \rfloor) + \lfloor n/4 \rfloor] + n = 3^2T(\lfloor n/4^2 \rfloor) + 3\lfloor n/4 \rfloor + n$

- 第 3 层：  
  $T(\lfloor n/4^2 \rfloor) = 3T(\lfloor n/4^3 \rfloor) + \lfloor n/4^2 \rfloor$，  
  代入得到：  
  $T(n) = 3^3T(\lfloor n/4^3 \rfloor) + 3^2\lfloor n/4^2 \rfloor + 3\lfloor n/4 \rfloor + n$

通过不断展开，规律逐渐显现出来。第 $k$ 层的展开形式为：

$
T(n) = 3^k T(\lfloor n/4^k \rfloor) + \sum_{i=0}^{k-1} 3^i \cdot \left\lfloor \frac{n}{4^i} \right\rfloor
$

步骤 2: 终止条件
递归终止于 $n$ 变得足够小的时候，例如 $T(1)$，通常是常数（假设 $T(1) = O(1)$）。当 $n/4^k$ 接近 1 时，递归结束。也就是说，递归的层数 $k$ 满足 $n/4^k \approx 1$，即 $k \approx \log_4 n$。

步骤 3: 计算复杂度
代入递归终止条件 $T(1) = O(1)$ 后，我们得到：

$
T(n) = 3^{\log_4 n} \cdot O(1) + \sum_{i=0}^{\log_4 n - 1} 3^i \cdot \frac{n}{4^i}
$

由于 $3^{\log_4 n} = n^{\log_4 3}$，我们首先得出主项为 $n^{\log_4 3}$。

接下来，我们计算求和项。该和式可以近似为一个几何级数，其主要增长项为 $O(n)$，因为：

$
\sum_{i=0}^{\log_4 n - 1} 3^i \cdot \frac{n}{4^i} \approx O(n)
$

步骤 4: 最终结果
综合以上结果，我们可以得到递归式的复杂度为：

$
T(n) = O(n^{\log_4 3})
$

使用对数换底公式，$\log_4 3 = \frac{\log 3}{\log 4} \approx 0.792$。因此，复杂度最终为：

$
T(n) = O(n^{0.792})
$

结论
递归式 $T(n) = 3T(\lfloor n/4 \rfloor) + n$ 的解为 $O(n^{0.792})$。

🌟借助递归树

目的：使展开过程直观化
流程：
画出递归树，然后求解：

每层总代价
树高：指的是递归树中最长路径的层数。在这个递归关系中，每次递归调用都会将问题规模减半，直到问题规模缩减到1。
叶子节点代价

一般总代价有三种情况：

由根节点主导
由叶子节点主导
由深度主导

例 3T(n/4) + Θ(n2)

$T(n) = 3T(n/4) + Θ(n^2)$：
为简化分析，我们将递归树中的$Θ(n^2)$这一渐近符号项替换为一个代数式$cn^2$ 。这里引入了第一个“不精确”因素，但是我们认为这不会影响最终结果。
于是我们将递归树变为$T(n) = 3T(n/4) + cn^2$。
为方便起见，我们还假定n是4的幂。这里又引入了一个“不精确”因素，但我们同样认为这不会影响最终结果。现在可以创建递归树，如下图所示。

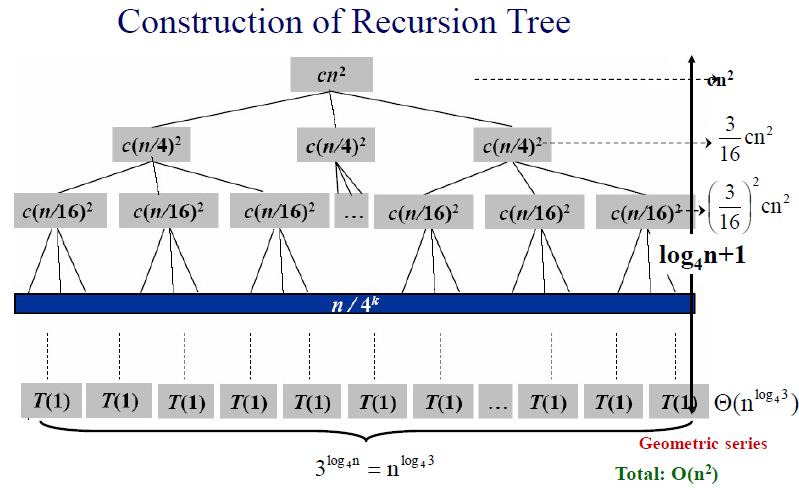
The fully expanded tree has $log_4n+1$ levels

每层的节点数是上一层的三倍,第k层的节点数为$3^k$。
每一层子问题规模是上一层的1/4,可以得到每层每个节点的代价。因此深度为$k$的结点，其子问题的规模为$n/4^k$
每一个结点对应一个规模为 $n/4^i$ 的子问题，每个子问题产生代价$c(n/4^i)^2 = cn^2/16^i$
每层总代价： 节点数×节点代价是每层代价,求得第k层代价为$(\frac{3}{16})^k cn^2$。
注意这里得到的代价是非叶子节点的代价。
当到达叶结点时，子问题规模减为$1$。假设叶结点深度为$k$，那么有$n/4^k = 1$得到$k=log_4n$ 所以叶结点深度为${\rm log}_4n$ ,这也说明整棵递归树的高度为 ${\rm log}_4n$
叶子节点的总代价:一个叶子节点的代价为T(1),想要求最底层代价还需要知道叶子节点的数量。
叶子节点的总数量是$3^{log_4 n} = n^{log_4 3}$ //第k层的节点数为$3^k$,树高是$log_4 n$

所以：递归树的总代价为（每一层代价加起来）

T(n)的总代价为$O(n^2)$

由于根结点对总代价的贡献为$cn^2$ ，所以根结点的代价支配了整棵递归树的总代价。

例 2T(n/2)+n2

$T(n)=2T(n/2)+n^2 (不妨设n=2^k)$
对应递归树为：

树高（层数）：树中最长路径，求总成本时和式的项数
令 $(n/2^k)^2 = 1$，解出 $k = \log_2 n$，则树高： $\log_2 n + 1$。
总成本： $O(n^2)$。

例 T(n/3) + T(2n/3) + n

$T(n) = T(n/3) + T(2n/3) + n$：
Fig.4.6

该递归树并不是一棵满二叉树，所以并不是每层的代价都为$cn$。随着递归树的层级越往下降，缺失的结点会越来多，这些存在缺失结点的层级的代价小于$cn$。

设树的层数为k，则$n * (2 / 3)k = 1$(最长路径)，解得$k = log3/2n$。另一方面，每层结点的数值之和都是O(n)，

因此$T(n) =log_{2/3}n• cn +n^{log_{2/3}2}= O(nlog3/2n) = O(nlogn)$。

很明显是根节点主导。

🌟练习题目

https://blog.csdn.net/yangtzhou/article/details/105339108

主定理（归纳流程）

分治法的主定理（Master Theorem）用于解决一些递归算法的时间复杂度问题。它适用于形如以下形式的递归关系：

\[T(n) = aT\left(\frac{n}{b}\right) + f(n) \]

其中：

$a$ 是子问题的数量；
$b$ 是子问题规模的缩小比例；
$f(n)$ 是分治法之外的额外工作量（通常是合并结果的过程）。

Master Theorem 提供了一个方法来确定这种递归关系的时间复杂度。具体来说，它基于 $f(n)$ 和 $n^{\log_b a}$ 的比较，分为三种情况：

Case 1: 如果 $f(n) = O(n^d)$，且 $d < \log_b a$，那么 $T(n) = O(n^{\log_b a})$。

这种情况下，递归的工作量主要由递归部分的大小决定。
Case 2: 如果 $f(n) = \Theta(n^d)$，且 $d = \log_b a$，那么 $T(n) = O(n^d \log n)$。

这种情况下，递归和合并步骤的工作量相当，时间复杂度为 $n^d \log n$。
Case 3: 如果 $f(n) = \Omega(n^d)$，且 $d > \log_b a$，并且满足一定的正则条件（例如，$a f(n/b) \leq k f(n)$ 对于某个常数 $k < 1$ 和充分大的 $n$），那么 $T(n) = O(f(n))$。

在这种情况下，合并步骤的工作量主导了整个时间复杂度。

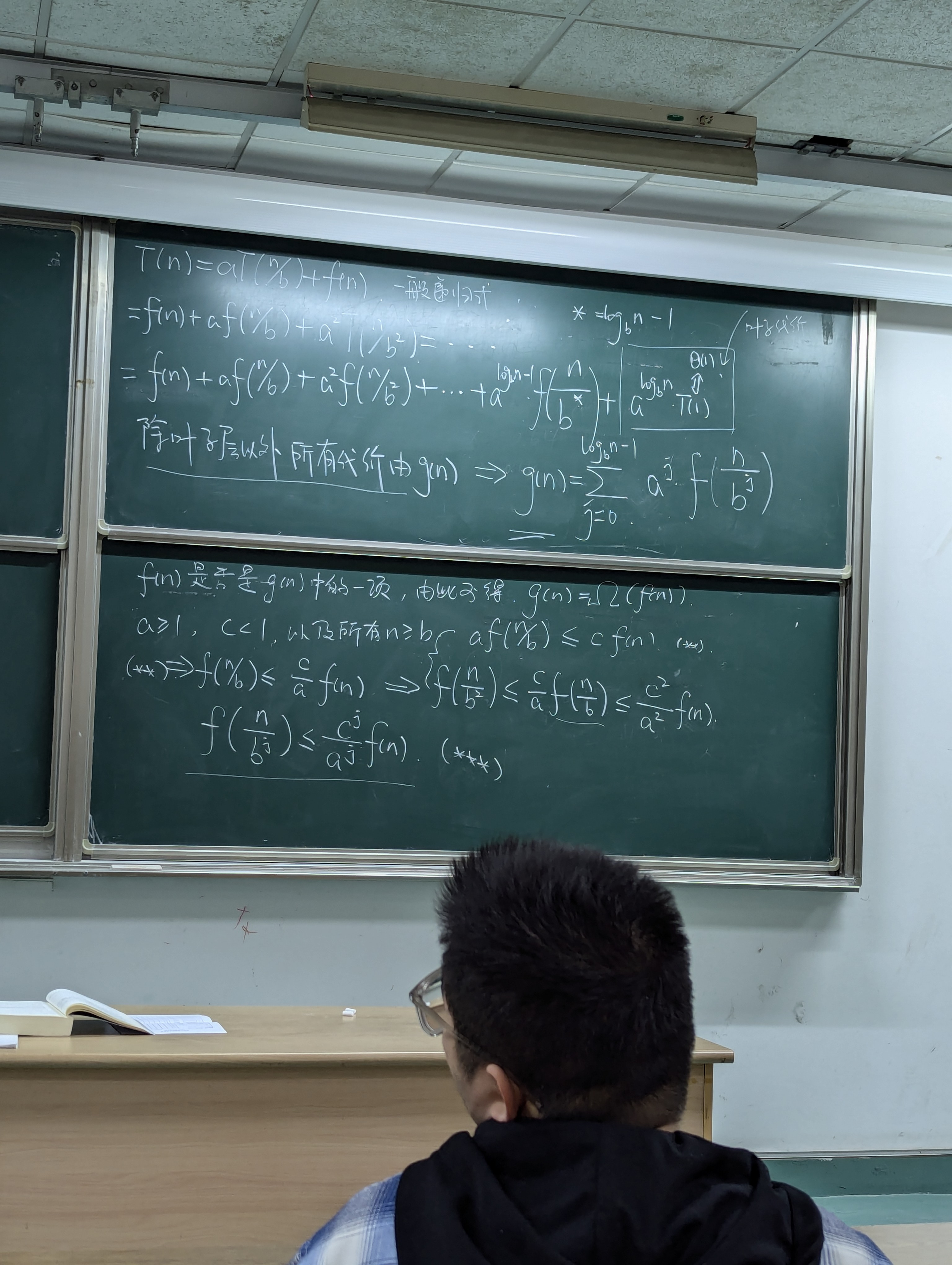
例外

递推关系的形式
我们给出的递推关系是：

\[T(n) = 2T(n/2) + O(n \log n) \]

注意到这里的额外项是 $O(n \log n)$，而不是单纯的 $O(n^d)$ 形式。这使得递推关系的右边项不符合主定理中的标准形式。

为什么不能直接应用主定理？
主定理要求递推式右边的项是一个简单的多项式（如 $O(n^d)$），但是在 $O(n \log n)$ 中，额外的对数项（$\log n$）让它与标准的多项式形式不同。因此，主定理不能直接应用于这个递推式。

为了更好地理解为什么主定理不适用，我们可以尝试将 $O(n \log n)$ 转换为其他形式：

主定理适用的情况：如果递推式的右边是单一多项式（如 $O(n^d)$），那么可以通过比较 $n^{\log_b a}$ 和 $n^d$ 来确定递推的解。
在 $O(n \log n)$ 的情况下：虽然我们可以通过其他方法（如递归树法）分析这个递推式，但主定理无法直接得出结果，因为我们需要考虑 $\log n$ 项的影响，而主定理本身并不处理对数项。

数学推导过程
为了求解递推关系 $T(n) = 2T(n/2) + O(n \log n)$，我们可以使用 递归树法 或 扩展主定理 来处理这种带对数项的递推关系。

使用递归树法
递推式的递归树可以按以下方式展开：

第 0 层（根）: 需要计算 $O(n \log n)$。
第 1 层：每个子问题大小为 $n/2$，总共有 2 个子问题，每个子问题需要 $O(n/2 \log(n/2))$，总共是 $2 \times O(n/2 \log(n/2)) = O(n \log n)$。
第 2 层：每个子问题大小为 $n/4$，总共有 4 个子问题，每个子问题需要 $O(n/4 \log(n/4))$，总共是 $4 \times O(n/4 \log(n/4)) = O(n \log n)$。

如此继续，每一层的复杂度都为 $O(n \log n)$，并且层数为 $\log n$（因为每次子问题大小减半）。因此，总的复杂度为：

\[T(n) = O(n \log n) \times \log n = O(n (\log n)^2) \]

因此，最终的时间复杂度是 $O(n (\log n)^2)$。

由于递推关系的右边项是 $O(n \log n)$ 而不是单项式 $O(n^d)$，主定理不能直接应用。我们需要通过递归树法等其他方法来推导出结果，最终得出 $T(n) = O(n (\log n)^2)$ 作为该递推关系的解。

相关分治算法

二分查找树ASL

ASL（Average Search Length）即平均查找长度

比较树的形状至于节点个数有关（二分查找是在树上比较，应该能理解树的含义了）

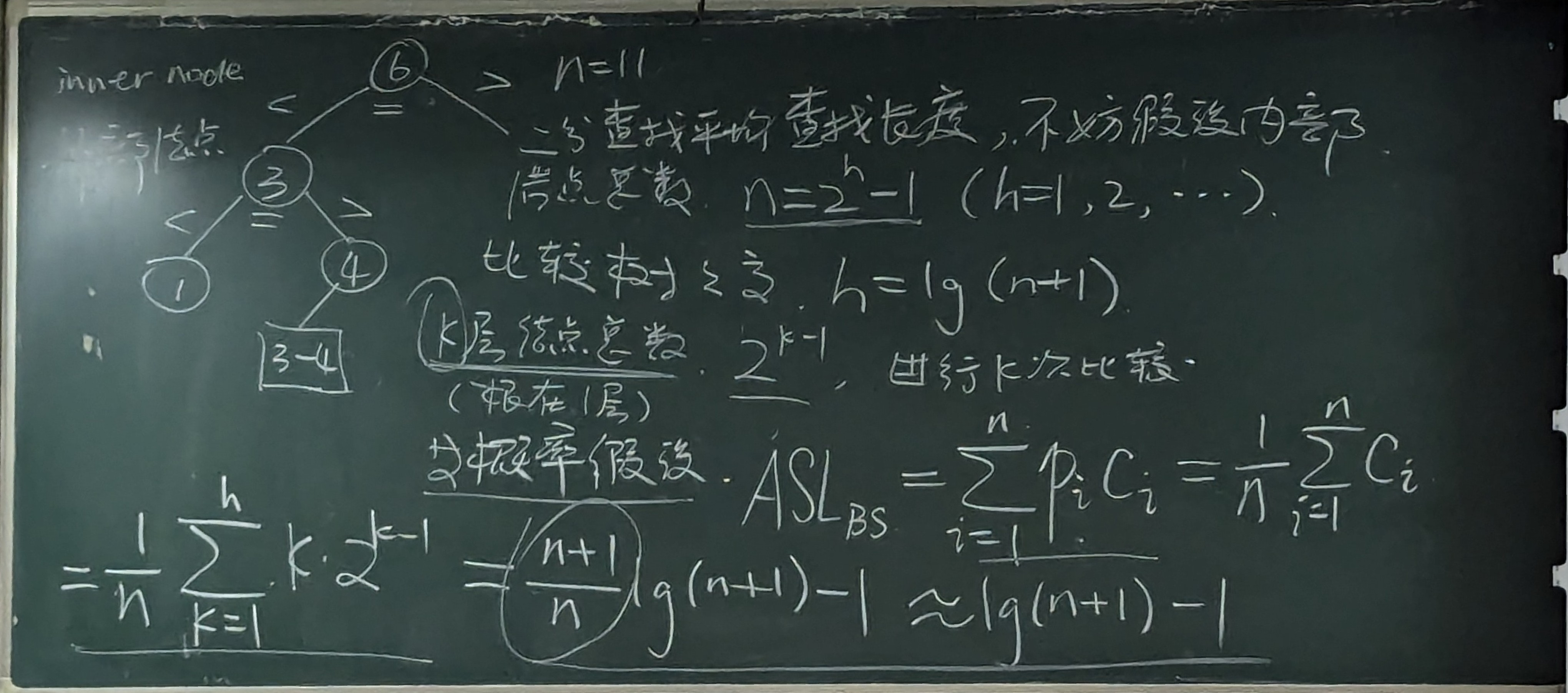
求解平衡二分查找树的平均查找长度 (ASL)

我们考虑一棵平衡二分查找树（如AVL树或红黑树），并分析如何计算其平均查找长度（ASL）。这里的平衡二分查找树保证树的高度是对数级别的，因此，ASL的计算过程与树的高度密切相关。

定义和公式
平衡二分查找树的平均查找长度（ASL）是所有节点从根节点到该节点的路径长度的平均值。假设树中有 $n$ 个节点，每个节点的路径长度为 $L_1, L_2, ..., L_n$，则 ASL 可以表示为：

\[\text{ASL} = \frac{L_1 + L_2 + \dots + L_n}{n} \]

树的高度与查找路径
对于一棵平衡二分查找树，树的高度通常是 $O(\log n)$，也就是说，树的深度不会超过 $\log_2 n$。此外，树是平衡的，因此大部分节点的深度不会远大于 $\log n$，而是分布在这个高度范围内。

树的高度（Height of Tree）：
假设树的高度为 $h$，那么树中的节点深度最多为 $h$，最少为 0（即根节点的深度为 0）。

树的节点深度分布：
假设树的结构是平衡的，每一层大致有相同数量的节点。平衡二分查找树的节点深度 $L$ 的分布大致是对数型的，即节点深度越深的节点数量越少。

节点深度的期望值
对于平衡二分查找树，节点深度分布呈现出类似对数分布的特点。树的深度 $h$ 为 $O(\log n)$，节点的深度越深，其数量越少。对于一棵平衡的二分查找树，平均查找长度 ASL 可以通过以下方式估算：

平衡树的高度大约为 $\log_2 n$。
在平衡树中，节点深度从根到叶节点呈现一种对数型分布，大多数节点的深度接近树的高度。

平均查找长度的推导
在平衡树中，树的深度通常是 $O(\log n)$，并且树的节点分布大致均匀，因此 ASL 的计算可以通过树的深度的平均值来推导。
深度分布的估算
平衡二分查找树的深度分布类似于完全二叉树。我们可以估算每一层的节点数量，并根据层数计算出节点的平均路径长度。假设树的高度为 $h$，并且树的节点深度大致符合以下分布：

第 0 层（根节点）：1 个节点，深度为 0
第 1 层：2 个节点，深度为 1
第 2 层：4 个节点，深度为 2
第 $i$ 层：$2^i$ 个节点，深度为 $i$

树的总节点数大约为 $2^0 + 2^1 + 2^2 + \dots + 2^h$，即：

\[n \approx 2^{h+1} - 1 \]

其中，$h = \log_2 n$。

计算ASL：
我们可以通过树的深度分布来计算平均路径长度（ASL）。对于每一层 $i$，该层的节点数为 $2^i$，且这些节点的深度为 $i$。因此，所有节点的路径长度的总和为：

\[\text{路径总长度} = 0 \cdot 1 + 1 \cdot 2 + 2 \cdot 4 + 3 \cdot 8 + \dots \]

这可以写成：

\[\text{路径总长度} = \sum_{i=0}^{h} i \cdot 2^i \]

因此，平均查找长度（ASL）为：

\[\text{ASL} = \frac{\sum_{i=0}^{h} i \cdot 2^i}{n} \]

最终结果
通过公式推导，可以得出平衡二分查找树的平均查找长度 $\text{ASL}$ 的期望值。对于平衡树，经过计算和近似，结果为：

\[\text{ASL} \approx 2 \log_2 n \]

这意味着在一棵平衡二分查找树中，平均查找长度大致为 $2 \log_2 n$。

矩阵乘法

朴素算法时间复杂度$O（n^3）$
通过简单的递归不能降低时间复杂度，证明过程如下：

思路：通过减少划分块的次数（也就是减少8）,就是Strassen算法（快速矩阵乘法）,具体方法可以看：https://blog.csdn.net/qq_42327795/article/details/114538451

要证明通过简单的递归方法不能降低矩阵乘法的时间复杂度，我们需要理解矩阵乘法的基础和递归的限制。我们将从以下几个方面展开说明：

标准矩阵乘法

假设我们有两个矩阵 $A$ 和 $B$，其维度分别是 $n \times n$ 和 $n \times n$。标准矩阵乘法的计算过程涉及 $n^3$ 次乘法和加法操作。具体来说，矩阵乘法的公式为：

\[C = A \times B \]

其中，$C$ 是结果矩阵，其每个元素 $c_{ij}$ 由下式给出：

\[c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj} \]

因此，对于每个结果元素 $c_{ij}$，我们需要进行 $n$ 次乘法和加法操作。由于矩阵 $C$ 中共有 $n^2$ 个元素，所以标准矩阵乘法的时间复杂度是：

\[T_{\text{standard}}(n) = O(n^3) \]

递归矩阵乘法的尝试

我们可能会考虑通过递归来优化矩阵乘法。例如，设想将矩阵 $A$ 和 $B$ 分成更小的块，然后递归地乘这些小块。

一种常见的递归矩阵乘法方法是 分治法。具体地，我们可以将 $n \times n$ 矩阵 $A$ 和 $B$ 分割成 $2 \times 2$ 小矩阵，然后计算这些子矩阵的乘积。

例如，对于矩阵乘法 $C = A \times B$，我们可以将矩阵 $A$ 和 $B$ 分割成四个子矩阵：

\[A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}, \quad B = \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} \]

那么，矩阵乘法 $C = A \times B$ 可以分解为：

\[C = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix} \]

其中，

\[C_{11} = A_{11} \times B_{11} + A_{12} \times B_{21}, \quad C_{12} = A_{11} \times B_{12} + A_{12} \times B_{22}, \quad C_{21} = A_{21} \times B_{11} + A_{22} \times B_{21}, \quad C_{22} = A_{21} \times B_{12} + A_{22} \times B_{22} \]

在这个递归方案中，我们可以继续对每个子矩阵进行递归计算，直到子矩阵的大小为 $1 \times 1$。这样一来，矩阵乘法的问题被分解为多个更小的子问题。

递归矩阵乘法的时间复杂度

如果我们将矩阵分割成大小为 $n/2 \times n/2$ 的子矩阵，那么每个子问题的计算将涉及 8 次乘法（每个子矩阵乘法产生两个结果矩阵的元素），以及相应的加法操作$O(n^2)$。因此，我们可以写出递归的时间复杂度：

\[T(n) = 8T(n/2) + O(n^2) \]

其中，$O(n^2)$ 是在每一层计算结果矩阵所需的加法和加权操作（例如计算 $C_{11}$ 等）。这可以通过递归树的方法来求解。

根据递归树法或主定理（Master Theorem），这个递归式的解是：

\[T(n) = O(n^3) \]

因此，使用简单的递归分治法进行矩阵乘法时，其时间复杂度仍然是 $O(n^3)$，与标准的矩阵乘法没有显著的改进。

为什么简单递归不能降低时间复杂度

虽然通过递归将矩阵乘法分解为多个子问题，但是递归并没有减少每个子问题的计算复杂度。每一层递归仍然需要进行大量的加法和乘法操作，导致总的计算量与标准矩阵乘法相同。具体来说，递归方法虽然分解了问题，但它没有改变每个子问题的工作量。因此，递归方法不能减少计算量，也就无法降低时间复杂度。

优化矩阵乘法：Strassen算法

要提高矩阵乘法的效率，不能仅仅依赖简单的递归。Strassen算法 是一种通过更聪明的分治法来降低时间复杂度的方法。Strassen算法将矩阵乘法的递归分解为 7 次矩阵乘法和一些加法操作，且减少了加法操作的数量。Strassen算法的时间复杂度是 $O(n^{\log_2 7}) \approx O(n^{2.81})$，比标准的 $O(n^3)$ 要优。

Strassen算法的核心思想是在递归的过程中，通过巧妙的矩阵组合，减少了矩阵乘法的次数，从而提高了效率。

总结

简单的递归分治方法虽然能将矩阵乘法分解为更小的子问题，但每个子问题的计算量和标准矩阵乘法相同，因此递归矩阵乘法的时间复杂度仍然是 $O(n^3)$。为了降低矩阵乘法的时间复杂度，我们需要更复杂的算法（如 Strassen 算法），而简单的递归分治方法无法有效地减少计算量，进而无法降低时间复杂度。

进阶问题

🌟找逆序对（考试）

计数逆序

二维空间最近点

如何从二维平面n个点中寻找距离最近的两个点？

通过主定理可以查看优化思路为优化合并过程

https://blog.csdn.net/weixin_45925418/article/details/116172454

posted @ 2025-01-02 11:14 kingwzun 阅读(93) 评论(0) 收藏举报

刷新页面返回顶部

kingwzun