OO第一单元作业总结

OO第一单元作业总结

一、作业梗概

​ OO第一单元作业的核心是表达式的处理及化简，三次作业不断迭代增添功能：

• 实现简单的(x的幂函数以及常数)的多项式括号展开
• 增添了对三角函数、sum求和函数以及自定义函数的需求，但有三角函数中只有常数因子或幂函数的限定
• 取消了第二次作业中的限定，要求可实现多项式与因子的互相嵌套

二、程序思路及结构分析

核心思路

• 递归下降：得益于第一次上机和训练助教给出的代码，让我学习到了递归下降这一关键理念，通过对多项式（Expr）、项（Term）、因子（Factor）的分层处理，实现了作业的主要任务“去括号”，这一点体现在代码中的Parse类。
• 表达式实时处理：此思路亦来自于实验代码，通过建立表达式处理类（Analysis/Lexer），模拟读一项理解一项的过程，对每一次读取数或者符号进行实时反馈，其中包括getOperation()、getSymbol()、getFactor()、getTri()等方法对可能读入的各种元素进行读取。
• 类型统一化：尽管递归下降的思路将处理分成了三个层次，但为了便于处理，笔者将三个层次返回值都设定为多项式，这样的好处是在进行加减乘以及指数运算时，可以保证两运算数间的类型保持一致，避免不同层级之间相互运算而导致程序混乱。笔者在本文中将这个体现基础的多项式的类称为基元。

第一次作业

• 分析：由于第一次作业明确声明指数始终不会超过8，因此笔者在设置存储基元的Factor类时，定义了一个长度为0-8的数组，即表示一个指数最高为8的x的多项式。

• UML类图：

  
  

• 度量分析

  • 类

  

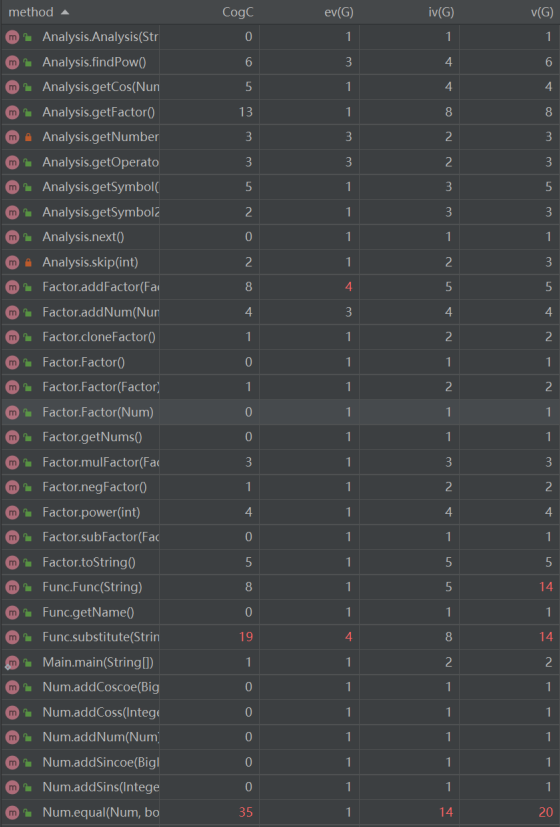
  • 方法
    

  • 程序优缺点分析及总结

    第一次作业整体来说较为简单，个人感觉是为了让同学们初步开始接触面向对象的第一次练手。由于可能出现的表达形式比较简单，因此我在学习了实验中助教给的示例代码后，仅用四个类就完成了第一次作业的编写。

    • 从程序来看，第一次作业优在简单明了，结构明晰，可读性高易理解，但劣在可拓展性较弱，例如在存储x幂函数的部分，直接简单粗暴地用了静态数组来存储，不利于之后指数无上限等的拓展。
    • 从结果来看，第一次作业由于比较简单，最后的正确性和性能的实现结果都令人满意，未曾有发现bug。

第二次作业

• 分析：第二次作业的难点为三角函数的存储以及sum函数、自定义函数的处理，为此笔者新增了Num、Pretreat、Func三个类
  • 三角函数的存储：由于三角函数内可能为常数或是x的幂函数，已不是第一次作业用一个数组所能支撑了，为此笔者写了一个Num类来作为基元存储，其可以理解为项的层级，存储了项的常数、x的指数以及用Hashmap分别存了三角函数内常数和幂函数的内容及其指数。
  • sum函数、自定义函数的处理：通过分析这两种函数可知，其皆可以通过一定规则的代换，将输入的expression处理成没有sum函数、自定义函数的形式，为此笔者设置了Func类来存自定义函数的函数名、自变量和表达式，再设置了Pretreat类对输入的初始expression进行处理，最终返回一个没有sum函数和自定义函数的expression_dealed供以后续的运算。
• UML类图

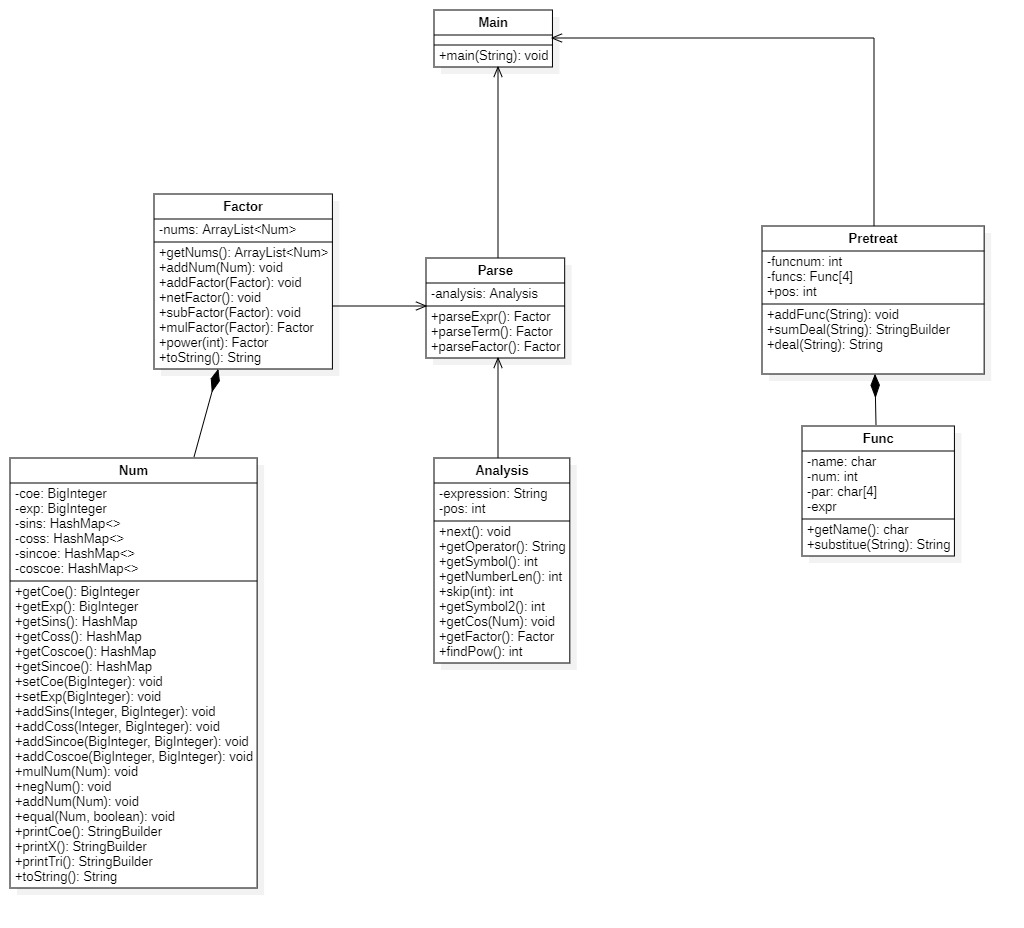
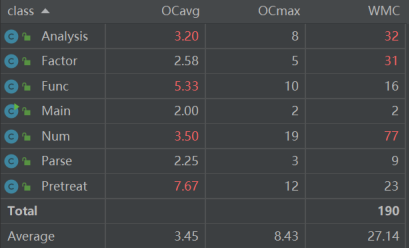
• 度量分析

  • 类

  

  • 方法

  

  • 程序优缺点分析及总结

    笔者认为第一次到第二次之间的跨度是最大的，三角函数的加入对原本的存储结构是一次巨大的冲击。在纠结了良久之后，笔者最终学习了讨论区同学暴力地将常数、x幂函数、三角函数全存在一个基元中的“暴力写法”，个人认为写得不尽人意，思路十分凌乱，为后续出bug埋下了伏笔。

    • 从程序来看，第二次作业存在诸多缺点，例如此种“暴力写法”过于生硬，只能说是为了解决第二次作业的任务刻意去实现，极大得缺乏可读性和可拓展性，这也是导致笔者在第三次作业中大量重构的原因，后面会讲到。除此之外，在第二次作业的迭代过程中，没有很好得兼顾到原有内容，这导致了在增添新功能时造成了代码的大量冗余，最后呈现出的就是代码乱七八糟的情况。
    • 从结果来看，本次作业出现了重大bug，虽然在修改bug后发现其实就是三角函数的处理中情况没有考虑完善，但我认为归根结底，是因为程序的复杂度过高而导致的思路不清晰所产生的bug。

第三次作业

• 分析：第三次作业的核心在于嵌套，一是三角函数内可以为多项式，二是自定义函数可以互相嵌套

  • 三角函数内的多项式：多项式的复杂性使得第二次作业的“暴力存储”做法不再有效，深思熟虑后我们可以发现，答案其实早就藏在原本的思路中，在前两次作业里，我们对于expression的处理有着Factor➡Term➡Expr➡Factor的递归嵌套层次结构，这不就可以用来作为我们存储多项式的结构么，因此笔者痛下决心对代码进行了大规模重构，删去了原有的Factor类和Num类，替换为以下三个新类：

    • Mi类：其仅为单个因子，可为常数、x^exp、sin()exp、cos()^exp，通过kind属性来表示当前Mi对象是什么种类，其中sin()、cos()有名为expr的Expr类对象体现了递归嵌套的结构特性
    • Term类：表示多个因子相乘的项层级，使用ArrayList存储多个Mi对象
    • Expr类：表示多个项相加的多项式层级，使用ArrayList存储多个Term对象

    如此这般构造，再实现同层级之间的运算以及每一层级对于下层元素的添加方法，最后将Expr类作为基元，即可完美地支持多项式嵌套的需求了。

  • 自定义函数互相嵌套：这一点其实较为简单，在第二次作业能实现对expression预处理的基础上，只需要对本次作业的expression重复进行多次预处理，直到新的expression中不再出现sum函数和自定义函数即可。

• UML类图

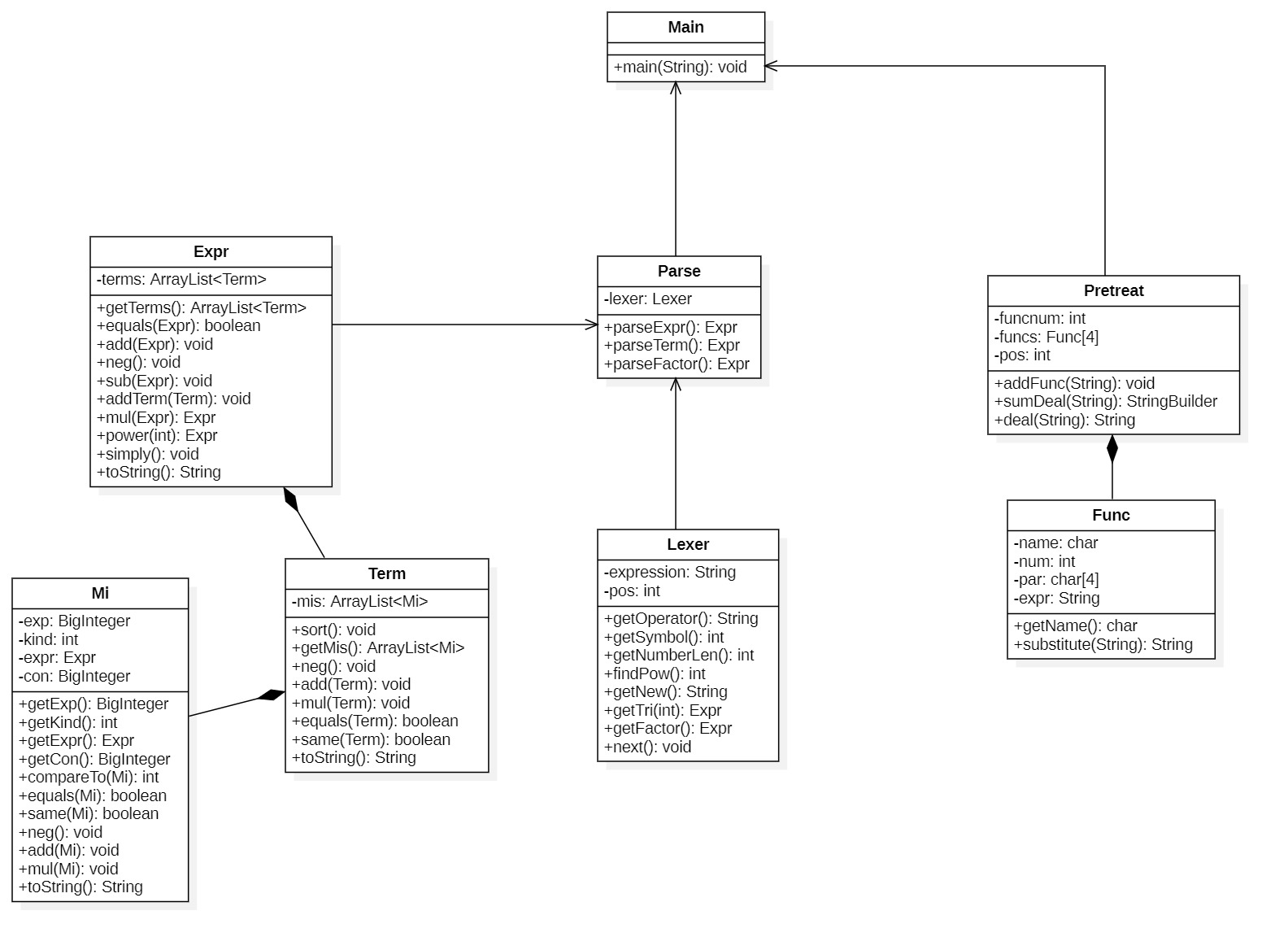
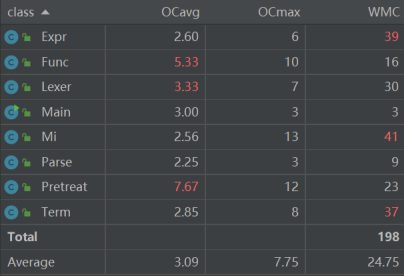
• 度量分析

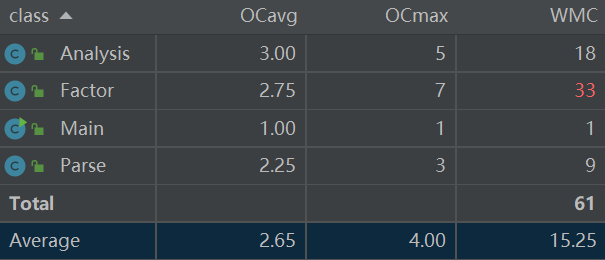
  • 类

  

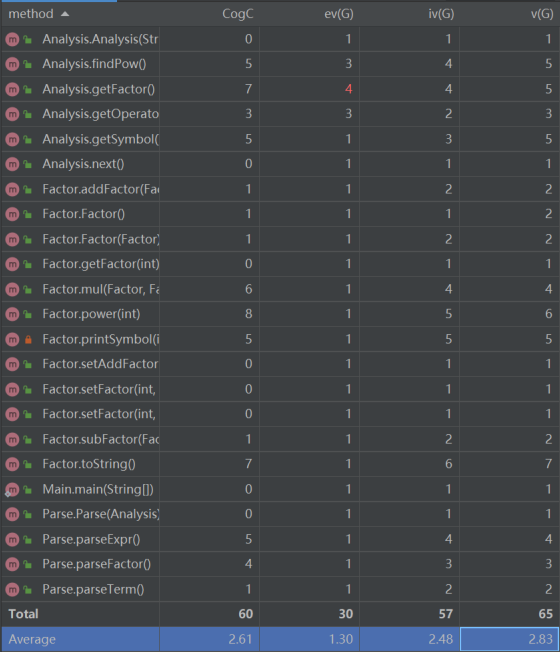
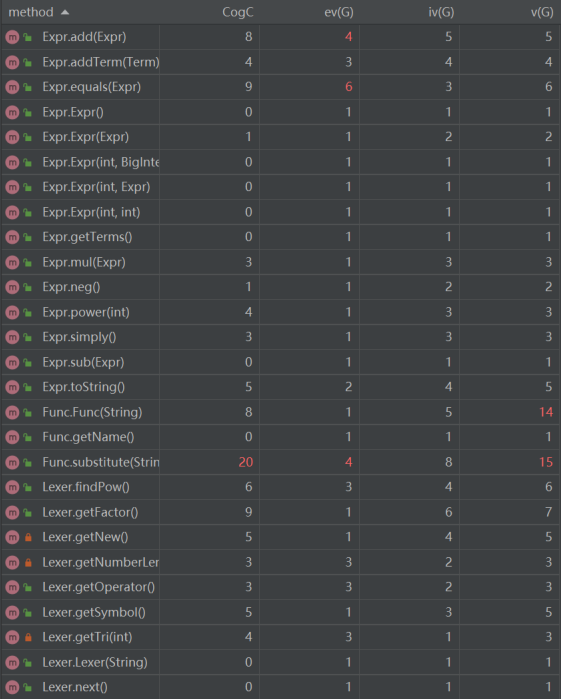
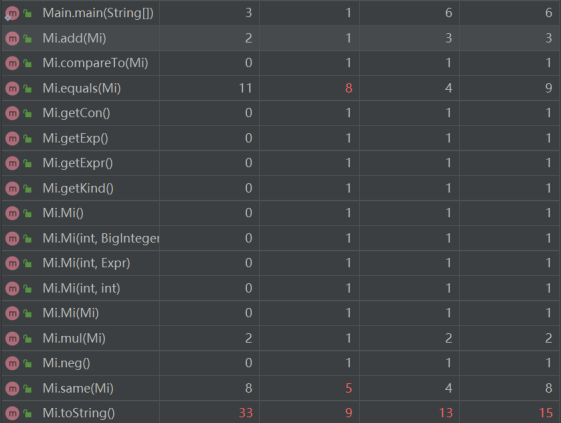
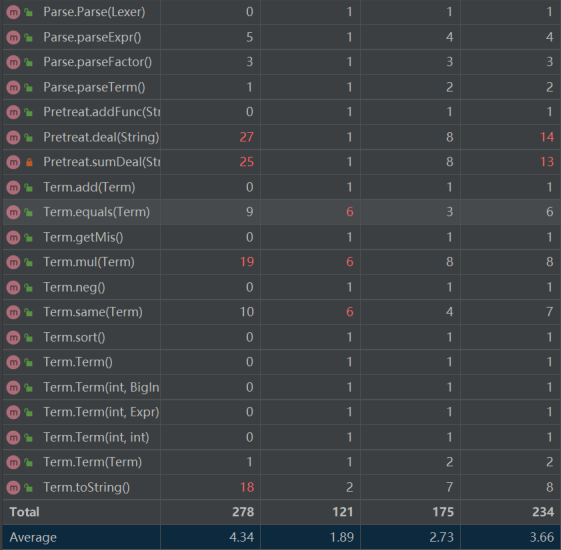
  • 方法

  
  
  

  • 程序优缺点分析及总结

    第三次作业的跨度较小，以至于许多同学在完成第二次作业时就已经实现了第三次的需求，变得十分轻松，但由于笔者的第二次作业完成得太烂，以至于在第三次作业中进行了大量重构，虽然花费了许多精力，但最后的结果是令人满意的。

    • 从程序来看，第三次采用了递归嵌套的结构来实现存储基元，笔者认为这是较为完美的一种写法，一是较优地实现了第三次的任务，二是程序结构明晰，以至于笔者在重构时一气呵成，未曾出现过因思路混乱而卡壳的情况，带来了一次令人身心愉悦的编程经历。
    • 从结果来看，第三次作业最后在互测过程中出现了一个小小的bug，是由于在优化三角函数中幂函数可去括号时，判断条件出错导致，总体来说差强人意。

三次作业对比分析

​ 三次作业的逐步迭代成型已在每次作业的分析中阐述，就不在此赘述了，让我们把目光放在程序复杂度和程序出bug的方面上。纵观三次作业，笔者在第二次作业中出现了重大bug，得到了极低的分数，抛开复杂度本身较高的expression预处理不谈，通过对比前文给出的度量分析可以发现，第二次作业在存储基元Num类上相较于另外两次有着较高的复杂度，直观来理解，笔者在第二次作业中将对多项式的计算全部丢入了Num类中，致使该类承载了过多混乱的功能，一方面导致了程序实现功能易出错，另一方面使得笔者在编写程序时思路混乱，最终导致了bug的出现。

​ 为此，笔者总结出一个往后写代码的经验：“物以类聚”——在我们构造程序结构时，一个类应当仅实现其紧密相关的功能，一但其功能开始繁杂，我们就应开始考虑将类继续细化，亦或是继承拓展，如此便能使得程序与程序员始终保持清晰。

三、互测

​ 互测是一次全新的体验，成功hack到人时着实给笔者带来了极大的成就感。

​ 笔者每周所花在写程序本身所耗费的时间过多，未曾有精力去模仿各位大牛写数据生成器以及自动评测机，所以没有加入“自动党”，最终只是略微通过读代码和一些简单策略来“找茬”，采用的策略核心是“盯紧优化部分”：

​ 这几次作业同学们在功能性其实都完成得很好，在hack了几次之后我渐渐发现大部人被hack问题主要都出在优化多项式长度时考虑不周，导致本因正确的结果出现奇奇怪怪的错误，例如符号不见了，0优化导致出现空项等现象，因此笔者在后来的互测阶段基本都是在尝试一些可能导致优化出错的数据，也取得了一定的hack成果。

四、心得体会

​ OO的第一单元就此落下帷幕，不知不觉竟已收获如此之多。笔者在过去这个月里，逐渐熟悉了java语言，初步掌握了面向对象的编程思想与形式，在作业中学习了递归下降的构造思路，体会到了大代码量的工程建立与迭代，同时还接触了互测和写博客这些以往未曾尝试的东西，可谓是度过了极其丰富的一个月。在此笔者要大力感谢OO课程的老师和助教们，为我们提供了如此完备的理论教育和作业安排，让我们在学习和实践中快速成长。

​ 当然，在过去的这个月里我有很多的不足，其中最大的问题就是没能克服面对大工作量的任务时的心理障碍，总是要拖到最后才开始着手任务，导致了OO这门课程乃至这一个月的学习节奏都变得拖沓。所谓“过而不能知，是不智也；知而不能改，是不勇也。”在接下来的OO单元中，我要努力做出改变，克服心理障碍，只要思路成型就动手去写，相信会这对我自身的学习节奏会有很大的助益。

五、写在最后

​ “是晚风，是余晖，是一道曙光，是未来可期”

​ OO的学习才刚刚开始，就让我们一同努力，一同进步吧！